并网双馈异步发电机转子侧变流器矢量控制系统的定子磁链定向

风能是一种不稳定的能源，如果没有储能装置或与其他发电装置互补运行，风力发电本身难以提供稳定的电能输出，因此一般大型风力发电机都要并网运行。为保证并网后电网和风电机组的运行效率、安全性和稳定性，风电机组与电网间的协调控制显得尤为重要。因此常将并网运行的变速恒频风电系统变流器的控制策略分为两个层次：外层控制器根据电力系统以及风电机组本身的安全可靠、优化运行的要求完成对风电机组电气部分运行参考值指令的给定；内层控制器则按外层控制器的输出指令采用双馈发电机定子磁链定向（图3-28c）和电网电压定向（图3-29c）矢量控制技术实现对控制参考指令值的跟踪。

变速恒频双馈异步发电机的控制包括两个控制系统：一是按定子磁链ψ_s定向控制转子侧变频器，使其输出频率为f_r、电压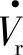为、电流为的三相交流电，对转子绕组供电，实现电机在指令速度ω_N∗（或功率P_s∗或电磁转矩T_e∗）和无功指令Q_s∗下的变速恒频运行，如图3_-28所示；另一个控制系统是按电网电压定向控制定子侧变频器，使其维持图3-26和图3-27中变流器直流中间电压V_dc为指令值V_d∗_c，同时又可使定子侧变频器从电网输入或向电网输出的有功P_s和无功Q_s跟踪指令值。

式（3-14）～式（3-17）、式（3-24）、式（3-30）～式（3-33）构成了双馈变速恒频异步发电机在d、q坐标系的数学模型，采用定子磁链定向控制转子侧变流器，为简化分析，图3-28a中将d轴取在定子磁链ψ_s方向上，则有

ψ_ds=ψ_s （3-37）

ψ_qs=0 （3-38）

图3-28 并网运行双馈异步发电机转子侧变流器按定子磁链定向矢量控制原理图

忽略定子电阻（即R_s=0），由图3-28a，定子感应电势瞬时值e_s（t）等于电网电压v_s（t）。e_s（t）=dφ_s（t）/dt=v_s（t），矢量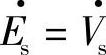。若电网系统容量很大，以至可认为v_s（t）是幅值为Vs的正弦波，则定子感应电势e_s（t）和电机定子磁链瞬时值ψ_s（t）也都应是同一频率的正弦波，若定子磁链幅值为φ_s，定子感应电势幅值为E_s，且ψ_s（t）=ψ_s sinω_st，则 （3-39）

e_s（t）=dψ_s（t）/dt=ω_sψ_s cosω_st=V_s sin（ω_st+90°） （3-40）

式中，V_s=ω_sψ_s=E_s。 （3-41）

因此，定子电压矢量幅值E_s=V_s与定子磁链ψ_s成正比。矢量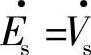超前磁链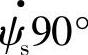。在图3-28a中已取出ψ_s在d轴上，ψ_ds=ψ_s，ψ_qs=0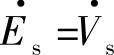，在超前d轴90°的q轴方向上，因此

V_ds=0 （3-42A）

V_qs=V_s=E_s=ψ_dsω_s=ψ_sω_s （3-42B）

由式（3-37）和磁链方程式（3-24）第一式得到：

式中，X_s=ω_sL_s，ψ_s=V_s/ω_s。 （3-44）

又由式（3-24）的第二式，ψ_qs=L_mi_qr-L_si_qs=0得到(www.xing528.com)

i_qs=i_qr ^Lm/L_s （3-45）

再由式（3-43）、式（3-45）、式（3-24）中转子磁链方程以及转子电压方程式（3-28）、式（3-29）得到：

式中，σ称为漏感因子，为

σ=1-L²_m/L_sL_r （3-50）

V_dr1=（R_r+σL_rP）i_dr、V_qr1=（R_r+σL_rP）i_qr分别为d、q轴转子电阻R_r、漏抗σL_rP的电压降。由式（3-32）、式（3-44）、式（3-45）得到：

由式（3-30）、式（3-31）、式（3-42A）、式（3-42B）、式（3-43）、式（3-45）得到

双馈发电机的控制可通过对发电机的转子绕组提供适当的交流电源电压V_dr、V_qr，产生相应的电流i_dr、i_qr、i_ds、i_qs和磁链ψ_dr、ψ_qr实现。由式（3-48）、式（3-49）可知，在一定的定子电压V_s和外加转子励磁电压V_dr、V_qr（角频率f_r，ω_r=2πf_r）下，可得到相应的转子电流i_dr、i_qr。通过式（3-43）、式（3-45），也可由定子电流i_ds、i_qs及定子电压V_s控制转子电流i_dr、i_qr，从而调控电机的电磁转矩T_e和电磁功率P_es，并利用运动方程式（3-33）研究双馈变速恒频异步发电机的机电动态特性。

风力发电机组运行中，由于风力、风向的随机性，不同的风速v工况下各有一个最佳的风机转速ω_Nopt或发电机的转速N_opt，在此速度下运行的风力发电机对风能的捕获效率最高，而且风力施予风力机的应力和磨损最小。因此应根据风速的不同而改变电机转速的指令值ω_N∗。另一方面为了调控发电机的输出功率P_s或电磁转矩T_e，亦可将发电机功率和转矩的指令值P_s∗、T_e∗作为控制系统的输入量。由于发电机的转速ω_N、转矩T_e、功率P_es（P_es=T_eω_s）都可由转子电流q轴分量i_qr控制（参见式（3-51）），因此并网运行时，风力发电机组的输入指令可以是ω_N∗、P_s∗或T_s∗。此外定子输出的无功功率Q_s也可独立调控，即通过无功功率闭环控制使实际输出的无功Q_s跟踪定子输出的无功指令Q_s∗。

图3-28b中与图3-25a一样，d轴超前定子A轴的相位角为θ_s，d轴超前转子a轴的相位角为θ_r，转子a轴与定子A轴的相位差角为θ_N。d轴取在定子磁链ψ_s方向上，超前ψ_s90°的定子电压即电网电压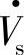则在q轴方向上，i_qr应是有功电流。图3-28c中转子有功电流指令i_q∗_r可以是发电机转速PI调节器的输出[使转速ω_N（N）跟踪指令值ω_N∗（N∗）]，也可能是来自发电机输出功率PI调节器的输出（使P_s跟踪P_s∗），或来自电磁转矩PI调节器的输出（使T_e跟踪T_e∗）。转子无功电流的指令值i_d∗_r来自输出无功功率Q_s的PI调节器的输出。根据不同的控制目标，图3-28c中检测发电机转子三相电流i_ar、i_br、i_cr经三相-两相静止变换后得到两相静止α、β坐标中的转子电流i_αr、i_βr，再经两相静止/两相旋转d、q坐标变换（S/T）得到转子电流i_dr、i_qr。

检测发电机输出电网电压v_sA、v_sB、v_sC经三相-两相静止变换后得到定子α、β电压V_αs、V_βs，再经两相静止直角坐标/旋转坐标K/P变换后得到定子电压幅值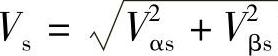及图3_-28b中电子电压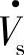超前A轴的相位角θ_u=arctanV_βs/V_αs=90°+θ_s，由此得到d轴超前定子A轴的相位角θ_s=θ_u-π/2。图3-28c中又将检测到的定子电压、电流V_sA、V_sB、V_sC、i_sA、i_sB、i_sC经3/2变换再经两相静止/旋转变换后（S/T）得到V_ds（0）、V_qs（=V_S）和i_ds、i_qs，输出发电机的有功和无功功率检测值Q_s、P_s。

图3-28c中由位置传感器检测转子α相与定子A相之间的相位差角θ_N（转速ω_N=dθ_N/dt）。由图3-28b得知，将θ_s与θ_N相减可得到d轴超前转子α轴的相角θ_r=θ_s-θ_N，转差速度ω_r=dθ_r/dt=dθ_s/dt-dθ_N/dt=ω_S（同步角速度）减去ω_N（转子旋转角速度）。由θ_r即可实现转子电压、电流两相静止-两相旋转S/T变换和两相旋转-两相静止T/S变换。

图3-28c中检测转子电流i_qr、i_dr，与其指令值i_q∗_r、i_d∗_r比较后经PI调节器输出V_qr1和V_dr1，分别作为转子电压指令V_d∗_r和V_q∗_r的一部分，即V_dr1和V_qr1。由转子电压方程式（3-48）和式（3_-49）可知，转子d轴电压指令V_d∗_r应由V_dr1即（R_r+σL_rP）i_dr和ω_rσL_ri_qr两部分构成，转子q轴电压指令值V_q∗_r应由V_qr1，即（R_r+σL_rP）i_qr、ω_rσL_ri_dr和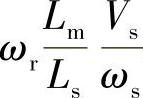三部分构成，其中ω_rσL_ri_dr、ω_rσL_ri_qr是d、q变量的交叉耦合量漏抗电压降（i_dr影响V_qr，i_qr影响V_dr），而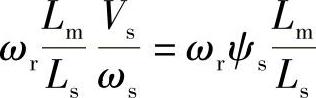是定子磁链ψ_s在转子绕组中产生的旋转电势。因为由式（3-25），定子电流i_s产生的全部定子磁链ψ_s=i_sL_s=i_sL_sσ+i_sL_m，ψ_s中与转子交链的定子磁链是ψ_m=i_sL_m=i_sL_sL_m/L_s=ψ_sL_m/L_s，频率为f_s的三相定子电流i_s所形成的与转子交链的旋转磁场（ψ_sL_m/L_s）以速度ω_s=2πf旋转，由图3-28b可知它与转子之间的相对速度为ω_r=dθ_r/dt，因此与转子交链的定子电流磁链ψ_sL_m/L_s在转子绕组中的旋转的电势E₂正是ω_rψ_sL_m/L_s。

图3-28c中的V_dr1、V_qr1分别作为d、q轴上转子电阻R_r和漏抗σL_rP的电压降补偿量。V_dr1为式（3-48）中的（R_r+σL_rP）i_dr，V_qr1为式（3-49）中的（R_r+σL_rP）i_qr。在图3-28c中按式（3-48）将V_dr1与ω_rσL_ri_qr相加得到转子d轴电压指令V_d∗_r，按式（3-49）将V_qr1与ω_r[σL_ri_dr+L_m/L_s（V_s/ω_s）]相加得到转子q轴电压指令V_q∗_r，再经两相旋转-两相静止T/S变换得到两相静止电压V_α∗_r、V_β∗_r，再经2/3变换得到a、b、c系统转子电压指令V_a∗_r、V_b∗_r、V_c∗_r，以此控制转子变流器输出的电压、电流实际值跟踪指令值V_d∗_r、V_q∗_r、i_d∗_r、i_q∗_r，转速ω_N（或转矩T_e，或功率P_s）跟踪指令值ω_N∗（T_e∗、P_s∗），定子无功输出Q_s跟踪指令值Q_s∗。例如，在图3-28c中，当实际转速ω_N<ω_N∗时，PI调节器输出的i_qr将减小，电机转子受到的电磁制动转矩T_e减小，使ω_N上升，跟踪ω_N∗；当Q_s<Q_s∗时，i_dr将增大，使i_ds增大，Q_s增大，跟踪Q_s∗。