变速恒频双馈发电机在d、q坐标系的数学模型优化

图3-24a为变速恒频双馈异步发电机系统原理电路。图中风力机经齿轮箱升速后驱动发电机转子以速度N旋转。交-直-交间接变频器从发电机端输入功率P₁，变频后经电刷、集电环向转子三相绕组a、b、c输出频率为f_r的三相交流电压V_r，功率为P_r。风力机供给转子的功率为P_m，发电机定子输出功率P_s由风力机供给转子的功率P_m和变流器供给发电机转子绕组的功率P_r两部分组成，P_s=P_m+P_r，故又称之为双馈发电机。

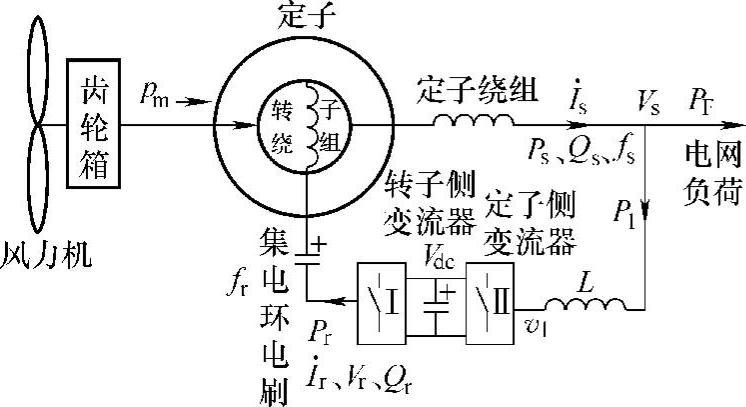
图3-24 变速恒频双馈异步风力发电系统原理电路

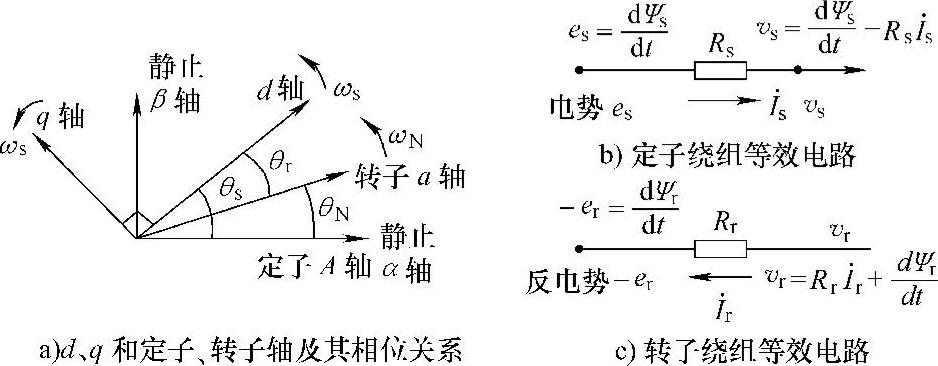
图3-25 定子、转子绕组等效电路及坐标系

不考虑变流器功率损耗时P_r=P₁，发电机向电网输出的功率P_F=P_s-P₁=P_s-P_r，又P_s=P_m+P_r，因此P_F=P_m+P_r-P_r=P_m，即风力发电系统中，发电机定子向电网输出的功率P_F等于风力机经齿轮箱输出的功率P_m，转子变频器只是从定子取出频率为f_s、电压为V_s的电功率P₁=P_r，经变频、变压后再输出给转子（f_r，V_r），以实现变速恒频发电（或电动）运行。

1.d、q系统中定子、转子电压平衡方程

图3-25b、图3-25c所示为定子绕组和转子绕组等效电路，定子绕组端电压v_s应等于定子绕组全部感应电动势e_s=dψ_s/dt减去电阻电压降R_si_s，转子绕组外加电压V_r应与转子绕组反电势-e_r=dψ_s/dt和电阻电压降R_ri_s平衡，由此可得到定子三相绕组和转子三相绕组电压平衡方程为

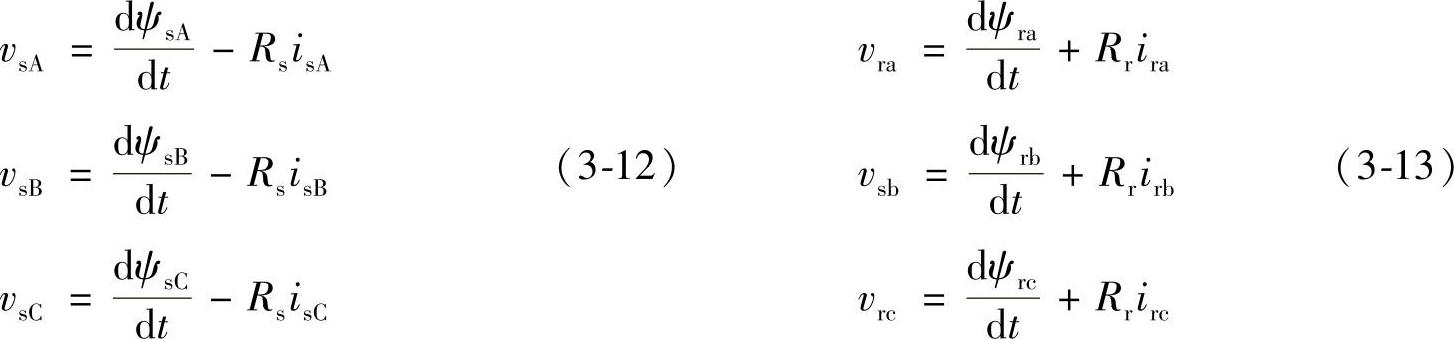
式中，ψ_sA、ψ_sB、ψ_sC，v_sA、v_sB、v_sC，i_sA、i_sB、i_sC和ψ_ra、ψ_rb、ψ_rc，v_ra、v_rb、v_rc，i_ra、i_rb、i_rc分别是定子、转子绕组的磁链、电压、电流；R_s、R_r分别是定子和转子绕组的电阻。采用第2章2.8节中的dq-ABC变换，图3-25a中以定子电流角频率ω_s=2πf_s旋转的d轴超前定子A相绕组轴的相角为θ_s=ω_st，ω_s=dθ_s/dt=2πf_s，d轴超前转子上α相绕组轴相角为θ_r=θ_s^-θ_N。d轴超前转子α轴的相对速度为ω_r=dθ_r/dt=dθ_s/dt-dθ_N/dt=ω_s-ω_N=2πf_r，f_r是转子三相绕组电流的频率，转子角速度ω_N=dθ_N/dt，利用2.8节中的经典Park变换式（2-75）～式（2-78），可将三相静止坐标电压、磁链、电流，变换为d、q坐标系电压，磁链、电流，将定子绕组A、B、C坐标系的电压方程和转子绕组的电压方程变为d、q坐标系的电压方程。

定子绕组：

转子绕组：

若转子转速为N，磁极对数为N_p，则转子相对于定子的电气角速度ω_N=dθ_N/dt=2πN_pN/60=2πf_N，f_N是与转速N对应的频率。图3-25a中以电气角速度ω_s=dθ_s/dt=2πf_s旋转的d轴超前定子A轴相位θ_s=θ_r+θ_N，因此有

ω_s=dθ_s/dt=2πf_s=dθ_r/dt+dθ_N/dt=ω_r+ω_N=2πf_r+2πN_pN/60 （3-18）

式中，ω_r=dθ_r/dt=2πf_r是频率f_r的转子电流在转子上产生的相对于转子的旋转磁场角速度。

由式（3-18）可知定子电流频率为f_s=f_r+N_pN/60 （3-19）

转子电流频率f_r=f_s-N_pN/60 （3-20）

转子转速N=60（f_s-f_r）/N_p=N_s-N_r （3-21）

定子电流频率f_s对应的同步速度为

N_s=60f_s/N_p=N+N_r （3-22）

转子电流频率f_r对应的旋转磁场转速为(www.xing528.com)

N_r=60f_r/N_p=N_s-N （3-23）

由式（3-20）可知，如果电机在发电工况下运行要求发电机定子电势频率固定为f_s=50Hz，当发电机如风力发电机转速N改变时，只要按式（3-20）改变向转子绕组供电的变频器的输出频率f_r即可。如果电机作电动机运行电网频率固定为f_s=50Hz时，只要改变转子电路变频器输出的转子电流频率f_r，即可调控式（3-21）中的电动机的转速N。

在三相静止坐标系中，电机定子磁链ψ_s、转子磁链ψ_r都是由定子三相电流i_sA、i_sB、i_sC和转子三相电流i_ra、i_rb、i_rc共同产生的。而相互垂直（正交）的d、q轴的定子、转子磁链ψ_ds、ψ_qs、ψ_dr、ψ_qr分别由d轴和q轴的定子、转子电流产生，d轴电流不产生q轴磁链q轴电流不产生d轴磁链。电感L的定义是单位电流产生的磁链，L=ψ/I，ψ=LI，所以有

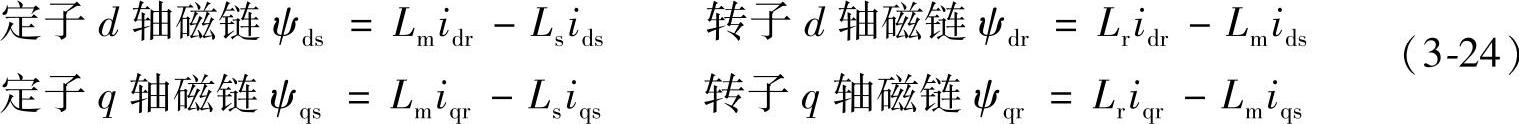
L_m是d、q座标系中同轴的定子与转子绕组之间的互感，L_s、L_r是定子、转子绕组自感，L_sσ、L_rσ是定子、转子绕组的漏感，则有

L_s=L_sσ+L_m，L_r=L_rσ+L_m （3-25）

定子电抗X_s=ω_sL_s，定子漏抗X_sσ=ω_sL_sσ。转子电抗X_r=ω_rL_r，转子漏抗X_rσ=ω_sL_rσ（折算到定子频率f_sω_s）。互感L_m对应定子频率的电抗X_m=ω_sL_m。

双馈变速恒频电机在稳态运行时，电压、电流、磁链空间矢量在d、q坐标系中的d、q分量都是恒定的，各项微分量都为零，这时将式（3-24）和式（3-25）代入式（3-14）～式（3-17）可得到d、q坐标系中定子、转子的电压平衡方程为

V_ds=ω_sL_si_qs-ω_sL_mi_qr-R_si_ds （3-26）

V_qs=-ω_sL_si_ds+ω_sL_mi_dr-R_si_qs （3-27）

V_dr=-ω_rL_ri_qr+ω_rL_mi_qs+R_ri_dr （3-28）

V_qr=ω_rL_ri_dr-ω_rL_mi_ds+R_ri_qr （3-29）

2.功率、转矩和运动方程

在两相旋转d、q坐标系中，由式（2-90）定子输出的三相有功功率P_s和无功功率Q_s为

在两相旋转d、q坐标系中，双馈发电机的转子磁场与定子电流所产生的电磁转矩T_e为

发电机电磁转矩T_e对应发电机的电磁功率P_e=T_eω_N/N_p（N_p为磁极对数，ω_N/N_p为转子机械角速度），若转子旋转时的摩擦阻力矩T_d=Dω，风力机输出给发电机转子上的机械功率P_m对应的驱动力矩为T_m，则由式（1-20F）可得发电机转子的运动方程为

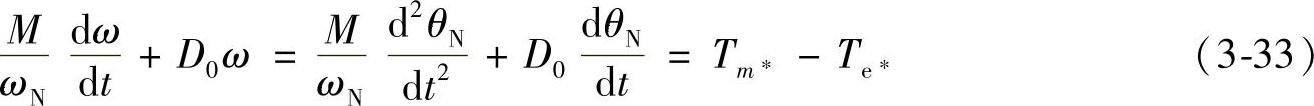
式中，ω_N为额定电气角速度即同步角速度；D₀为摩擦阻尼矩系数；θ_N为图3-25a中转子α相轴与定子A相轴之间的相位角，转子旋转的电气角速度ω=dθ_N/dt，转子转速N=60f_N/N_p，f_N为转速N所对应的频率；T_m∗、T_e∗分别为风机驱动机械的转矩标幺值和发电机电磁转矩标幺值。