特点比较：2.8.4d、q坐标系与α、β坐标系

1）采用变换式（2-59A）（变换式有系数2/3）和反变换式（2-61A）（变换式前系数为1）的经典Park变换后，变换前后功率不守恒，这是经典Park变换的第一个特点。为了使经典Park变换前后系统功率不变，可选用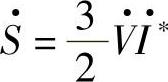定义d、q坐标系功率，即将两相功率v_di_d+v_qi_q或v_αi_α+v_βi_β增大3/2倍。如果经典d、q变换阵C_3s-2r前的系数不取为2/3而取为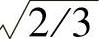，这时其反变换阵C_2r-3s前将有系数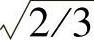，这就使v_Ai_A+v_Bi_B+v_ci_c=v_di_d+v_qi_q=v_αi_α+v_βi_β，即变换前后功率守恒，这时的d、q变换称为正交Park变换。因此，采用正交Park变换时按常规定义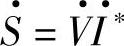也可得到式（2-88）～式（2-90）。

2）采用两相d、q和α、β经典Park坐标变换的第二个特点是：按经典Park变换式的定义，i_A、i_B、i_C，i_d、i_q和i_α、i_β，分别是电流空间矢量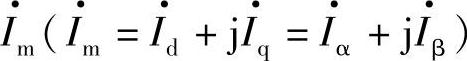在三相静止坐标系中A、B、C轴线上、在d、q轴和α、β轴上的分量（投影）。v_A、v_B、v_C，V_d、V_q和V_α、V_β则是电压空间矢量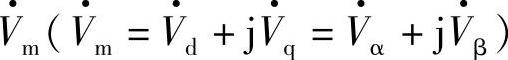在各自坐标轴上的分量（投影）。电压空间矢量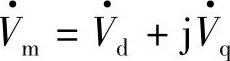，电流空间矢量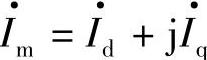，它们在A、B、C轴上的投影即其分量V_d、V_q、I_d、I_q在A、B、C轴上的投影之和就是v_A、v_B、v_C和i_A、i_B、i_C。同理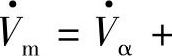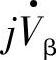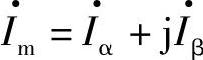，，它们在A、B、C上的投影即其分量V_α、V_β、I_α、I_β在A、B、C轴上的投影之和就是v_A、v_B、v_C和i_A、i_B、i_C。由于d、q轴正交，α、β轴正交，故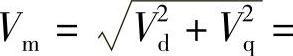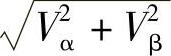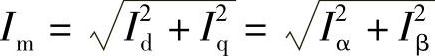，，所以采用经典Park变换后的空间矢量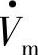、I·_m的幅值V_m、I_m就是A、B、C系统各相电压电流的幅值。

3）采用式（2-59A）～式（2-62）的经典Parkd、q变换的第三个特点是：A、B、C三相静止坐标系中的基波电压、电流变换到旋转的d、q坐标系后对应的电压、电流v_d、v_q、i_d、i_q是直流，A、B、C三相静止坐标系中n次谐波电压、电流变换到旋转的d、q坐标系后对应电压、电流是n-1次谐波电压、电流。在静止A、B、C系统中的基波和n次谐波变换到静止的α、β系统后，基波仍为基波，n次谐波仍为n次谐波。由经典Park变换及反变换式中个坐标电压、电流数学关系即可得到以上结论。(www.xing528.com)

在物理概念上，由于图2-20d中，d、q坐标轴以速度ω旋转，静止的A、B、C三相合成基波电压（电流）相量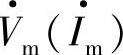也是以速度ω旋转，因此d、q坐标与基波矢量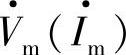相对静止，故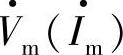在d、q坐标轴上的分量（投影）V_d、V_q、i_d、i_q应是直流量。在A、B、C坐标中的n次谐波三相合成的旋转矢量以速度nω旋转，它与d、q轴的相对速度为（n-1）ω。因此A、B、C中的n次谐波电压、电流变换到d、q系统后应是n-1次谐波电压、电流。同理由于α、β坐标系的α、β轴是静止的，故i_A、i_B、i_C变换到α、β坐标系后的电压、电流频率不变，基波仍为基波，n次谐波仍为n次谐波。

采用两相坐标系电压平衡方程和功率方程，如式（2-63）、式（2-64）、式（2-90），可以简便地研究三相电力电子变流系统和电力电子补偿控制系统的运行特性，同时利用这种两相正交的电压（电流）构建控制系统也适宜于采用先进的控制策略，使电力电子变流系统（逆变、整流）和电力电子补偿控制系统获得优良的控制特性。