电机坐标系电压平衡方程：旋转与静止坐标系对比

图2-20d中示出了三相静止A、B、C坐标系，两相旋转d、q正交坐标系和两相静止α、β正交坐标系的坐标轴。图中取A相轴线固定在水平方向上，三相静止坐标A、B、C轴线相差120°，取两相静止正交的坐标轴的α轴固定在静止的A轴方向上，β轴超前A轴（α轴）90°；取以速度ω旋转的d、q正交坐标轴的q轴超前d轴90°，d轴超前静止的A轴的相位角θ₂=ωt，即d、q轴相对于A、B、C轴以dθ₂/dt=ω的速度旋转。在三相交流系统中，幅值为I_m（V_m）的三相电流（电压）瞬时值i_A、i_B、i_C（v_A、v_B、v_C）可用一个在空间以角频率ω=2πf旋转的幅值为I_m（V_m）的电流（电压）空间矢量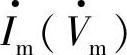在A、B、C绕组轴线上的投影表示，如图2-20d所示。图中将d轴取在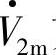方向上。若首端电压的空间矢量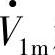超前电流空间矢量I·_m的相位角为φ₁，末端电压的空间矢量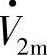超前I·_m相位角为φ₂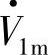，超前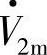的功角为δ，则电压空间矢量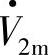、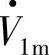以及电流空间矢量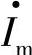都随d、q轴以角速度ω=2πf同步旋转。A、B、C三相电压、电流瞬时值v_2A、v_2B、v_2C、i_A、i_B、i_C、v1A、v1B、v1C可用以速度ω旋转的电压、电流空间矢量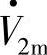、、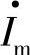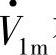在A、B、C轴上的投影表示。

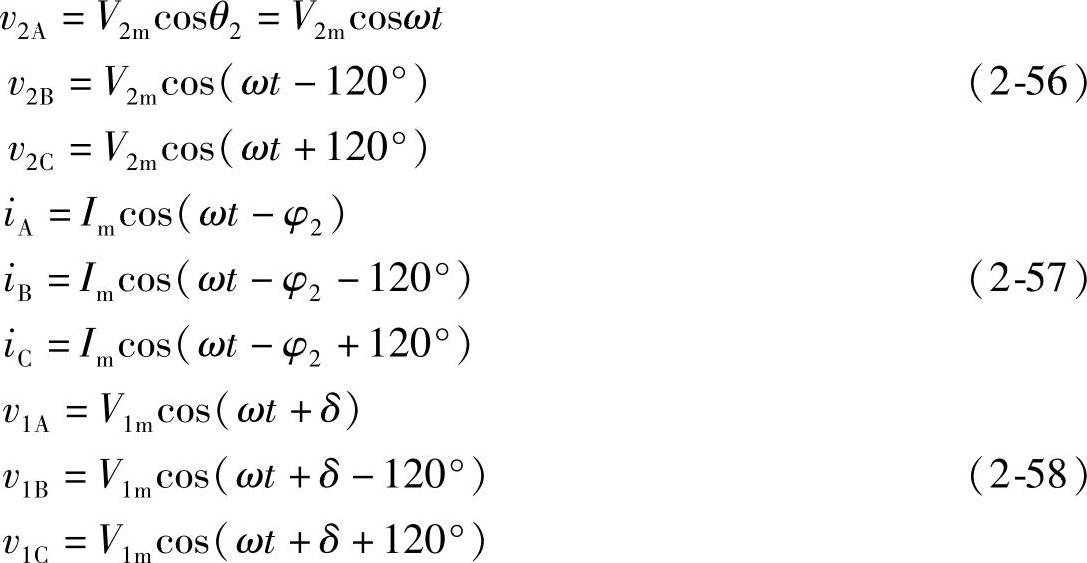
引入两相d，q旋转坐标系，用d、q坐标系中新的电流i_d、i_q及i₀代替三相静止坐标系中的i_A、i_B、i_C，并定义i_d、i_q、i₀与三相静止坐标系中A、B、C三相电流i_A、i_B、i_C有以下以Park命名的经典Park变换关系：

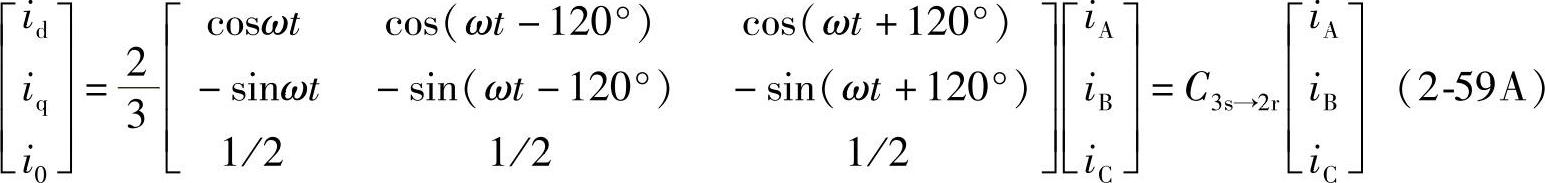
式中，ωt=θ₂，θ₂是以ω旋转的d轴超前静止的A轴的相位角。三相静止A、B、C坐标系中的电流i_A、i_B、i_C，变换到两相旋转d、q坐标中的i_d、i_q、i₀的变换阵C_3s→2r为

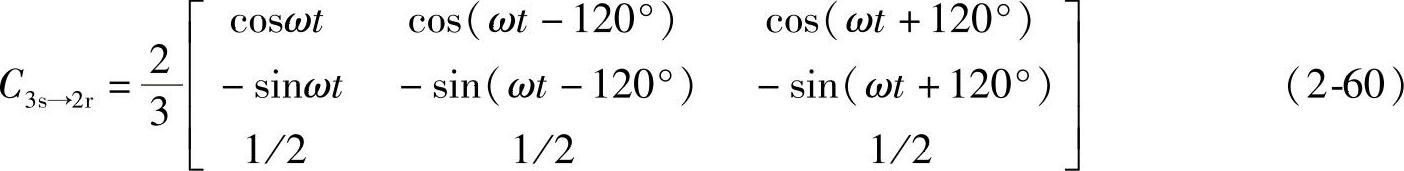
采用同一变换式可将三相电压v_1A、v_1B、v_1C、v_2A、v_2B、v_2C变为V_1d、V_1q、V₁₀、V_2d、V_2q、V₂₀：

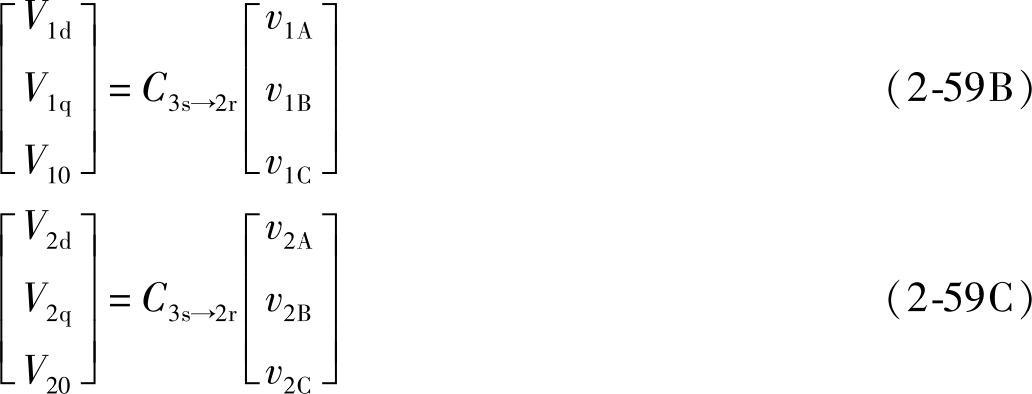
由式（2-59）可求得经典Park变换的反变换式为

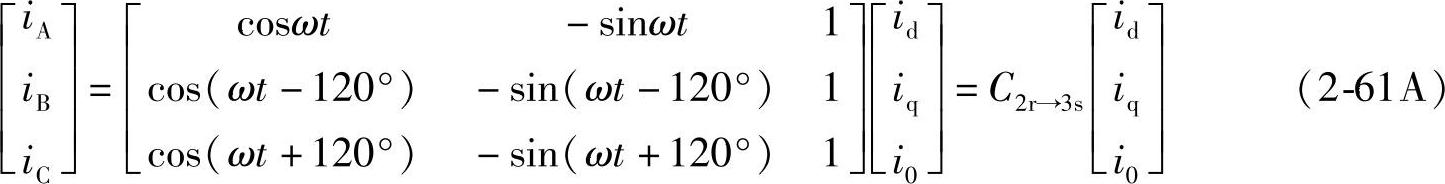
式中，将两相旋转d、q变量变为三相静止A、B、C变量的反变换阵：

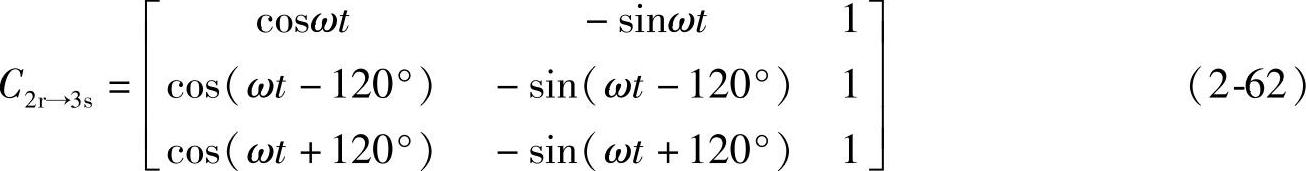
采用同一反变换式C_2r→3s可将V_1d、V_1q、V₁₀变为v_1A、v_1B、v1C；将V_2d、V_2q、V20变为v2A、v2B、v_2C：

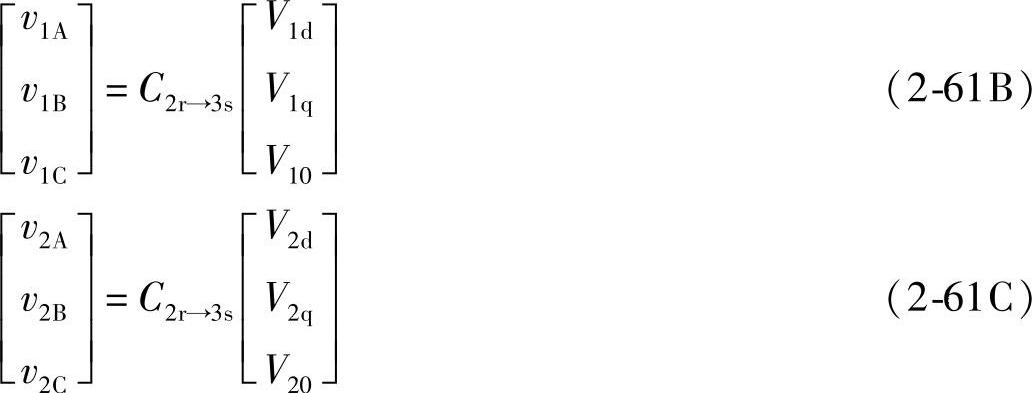
将式（2-61A）、式（2-61B）、式（2-61C）中的i_A、i_B、i_C代入式（2-54），可得到d、q两相旋转坐标系中的电压平衡方程，即

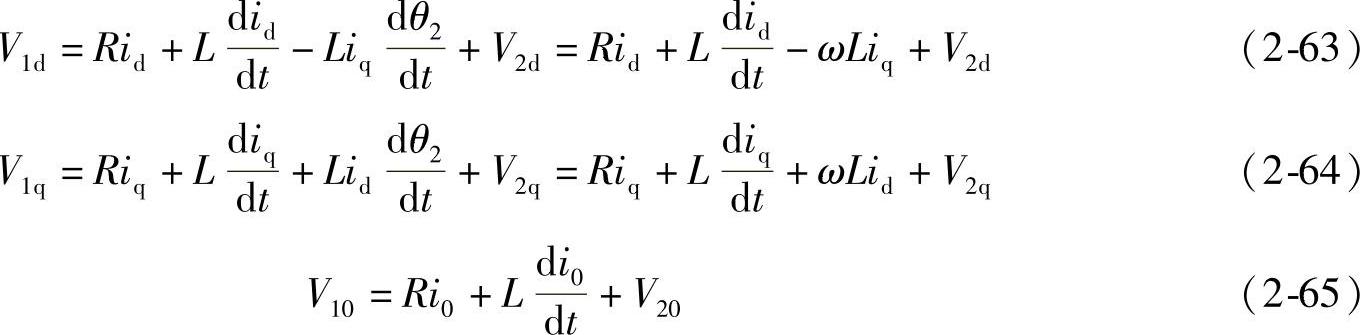
式中，θ₂=ωt，dθ₂/dt=ω。

式（2-65）独立于式（2-63）和式（2-64），可单独求解。因此在d、q坐标系中，只有两个相关的电压方程和两组正交的d、q电压、电流变量。如果像图2-20d中所示取d轴在某一电压空间矢量方向上，如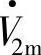取在d轴上，则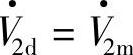，V_2q=0。这时系统特性的分析研究、计算与采用A、B、C三个电压平衡方程相比较要简便得多，同时在两相旋转坐标系中设计控制系统，实现许多控制策略还能获得优良的静、动态特性。

如果引入两相静止坐标系（α，β），取α轴与A相轴线重合，β轴超前A轴（α轴）90°，定义

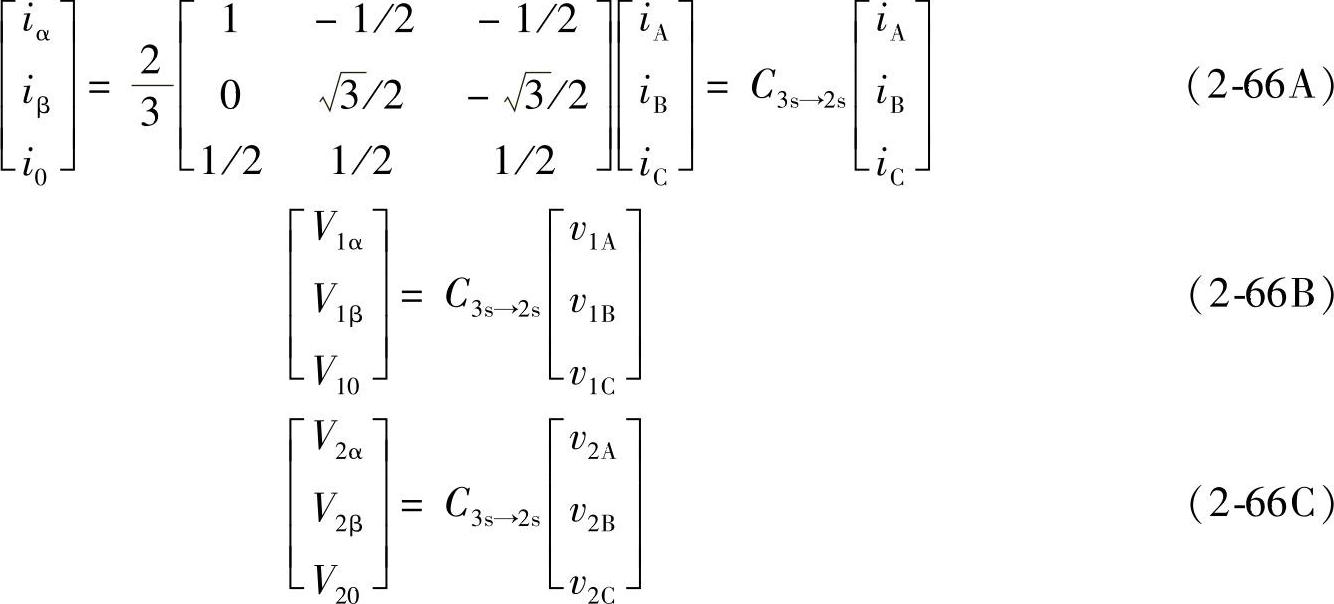
由式（2-66）可求得反变换式为

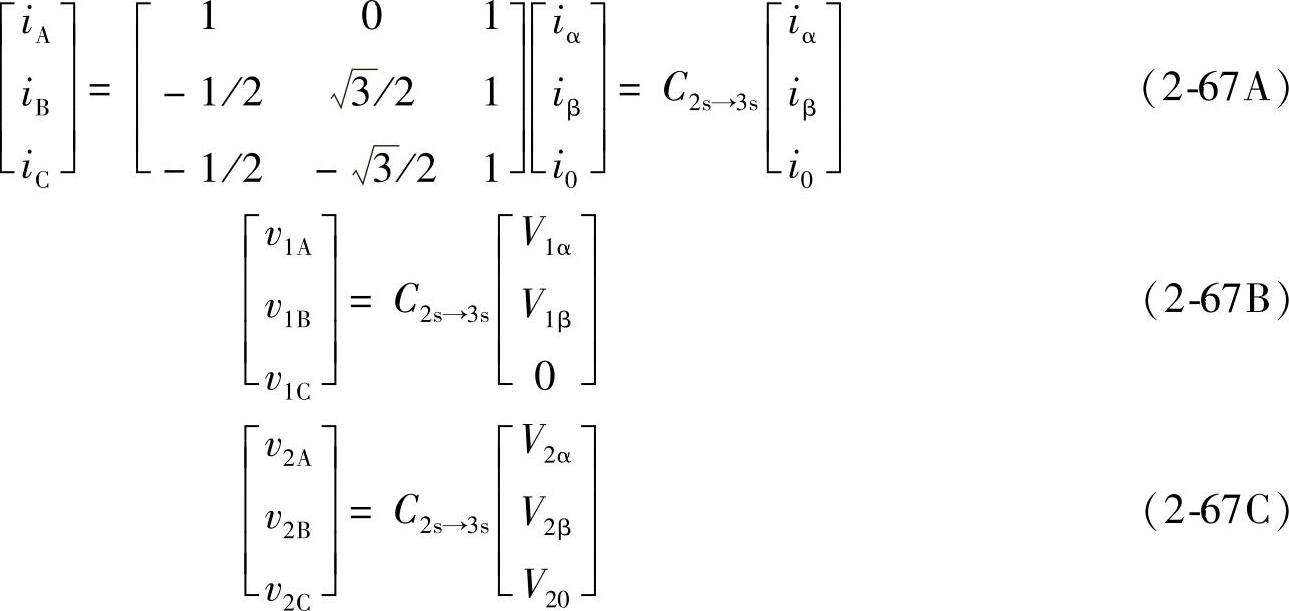
以上三相静止坐标系电压、电流变到两相静止坐标系的电压、电流变换阵C_3s→2s及反变换阵C_2s→3s为

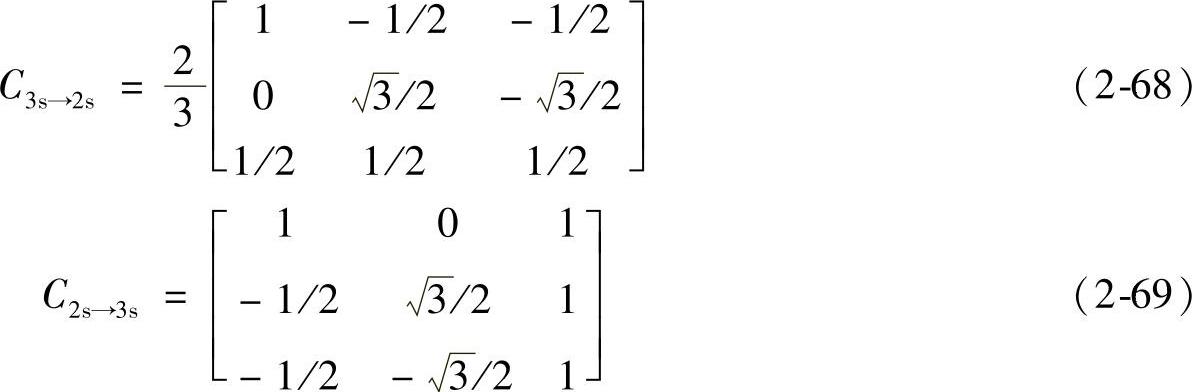
在式（2-59A）中令ωt=θ₂=0，即d轴固定在A轴上，则原两相旋转d、q轴即成为两相静止α、β轴，这时式（2-59A）中的i_d成为i_α，i_q成为i_β，变换阵C_3s→2r成为C_3s→2s，变换阵C_2r→3s成为C2s→3s两相旋标d、q正交坐标系电压平衡方程变为两相静止α、β正交电压平衡方程。

把A、B、C三相静止坐标中的电压平衡方程式（2-54）中的变量i_A、v_1A、v_2A用式（2_-67A）、式（2-67B）、式（2-67C）中的第一式的i_A、v_1A、v_2A代换，即可得到α、β两相静止坐标系中的电压方程为

将式（2-67A）的i_A、i_B、i_C代入式（2-59A）的i_d、i_q得到

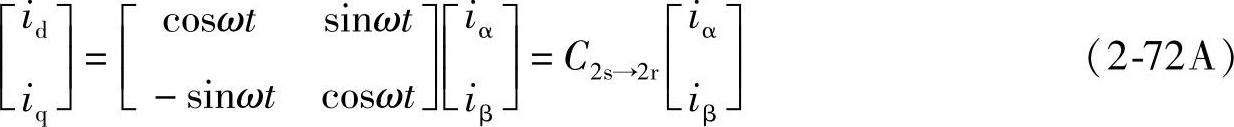
两相静止αβ-两相旋转dq变换阵C_2s→2r为

同理

由式（2-72）可求得反变换式为(https://www.xing528.com)

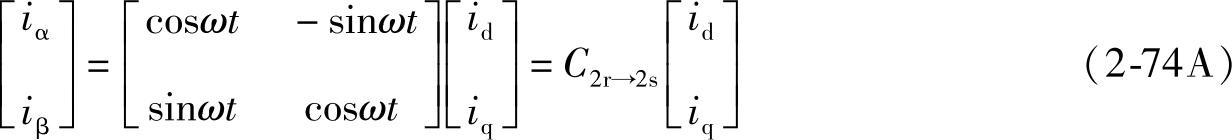
两相旋转dq-两相静止αβ变换阵C_2r→2s为

同理

如果三相系统无中线或三相电流平衡（即i_A+i_B+i_C=0），则式（2-59A）中i₀=0。如果三相系统三相电压平衡（即v_A+v_B+v_C=0），则式（2-59B）、式（2-59C）中V₁₀=0，V₂₀=0。这时式（2-59）、式（2-60）、式（2-61）、式（2-62）、式（2-66）、式（2-67）、式（2-68）、式（2-69）可简化为

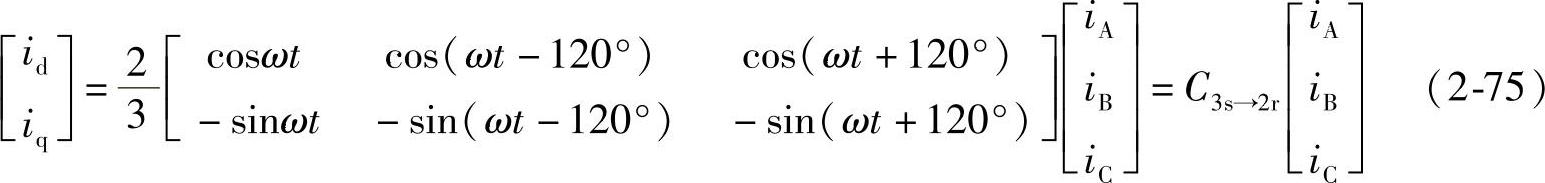
变换阵

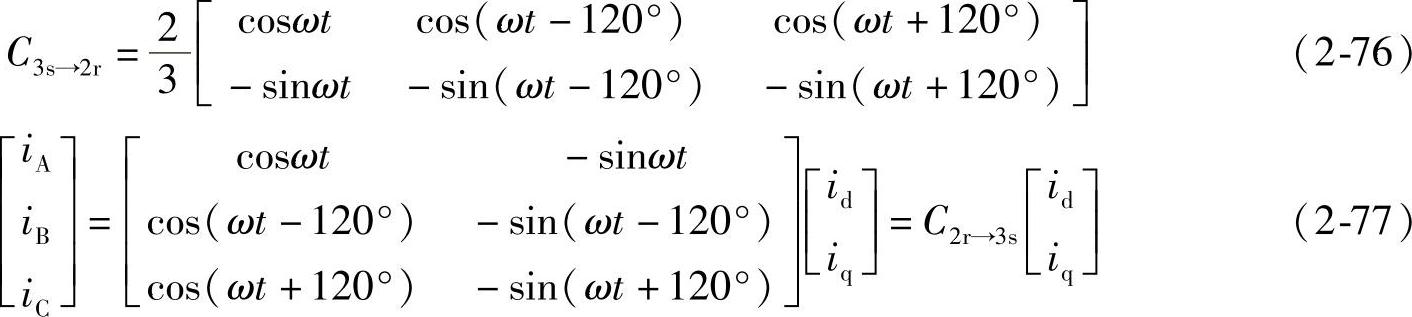
反变换阵为

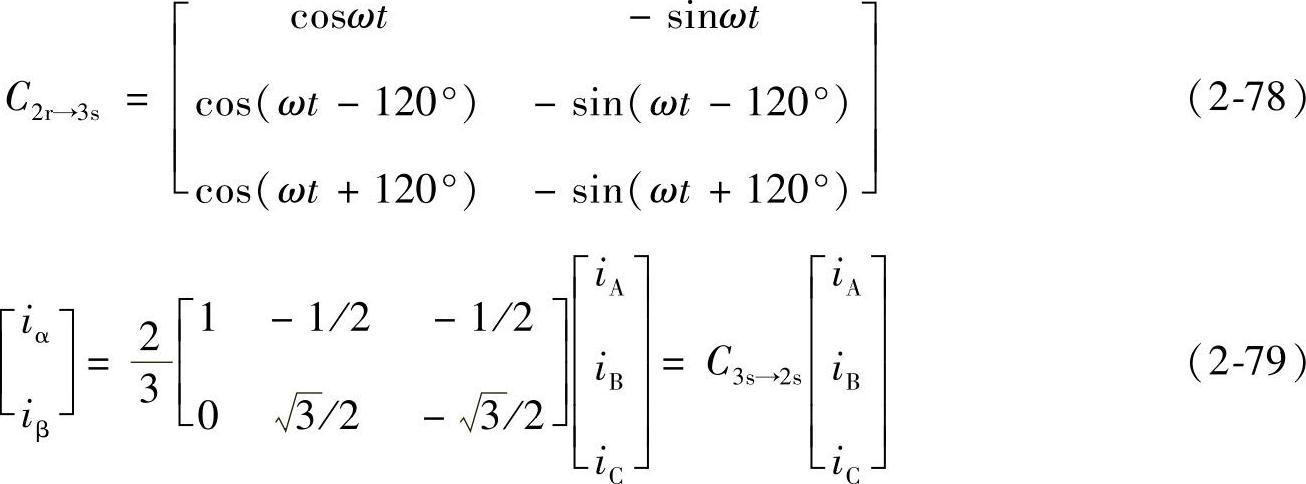
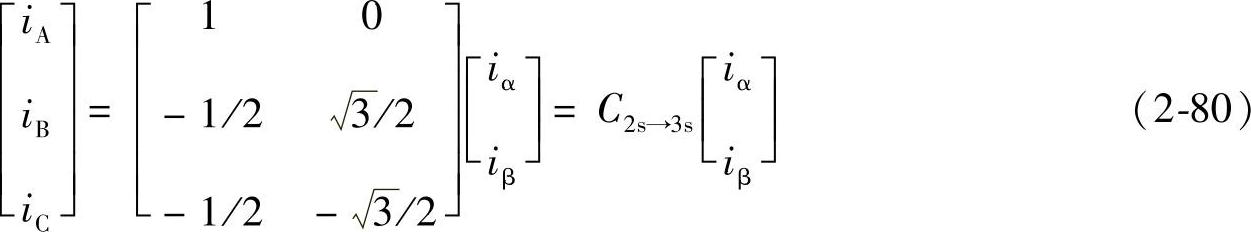
三相静止-三相静止变换阵为

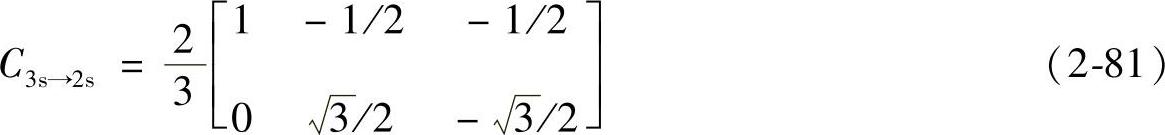
反变换阵为

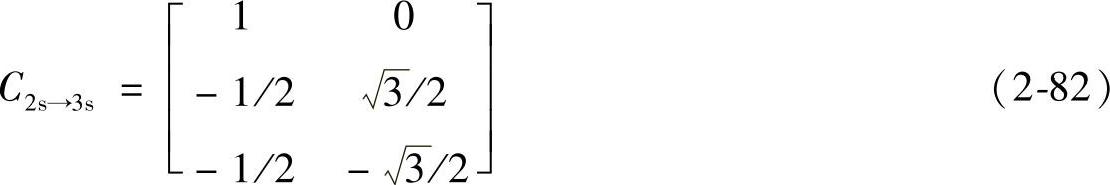
由式（2-63）、式（2-64）的d、q变量瞬时值电压平衡方程，可求得空间矢量电压平衡方程。

在图2-20d中，d轴超前A轴相位角θ₂=ωt，则空间电压矢量为

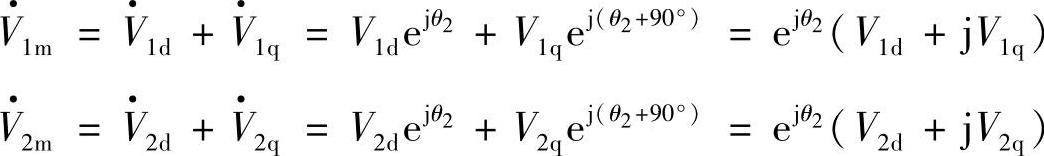
空间电流矢量为

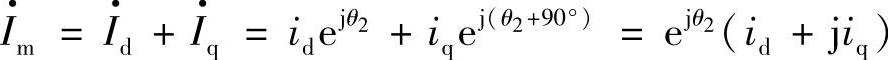
则有

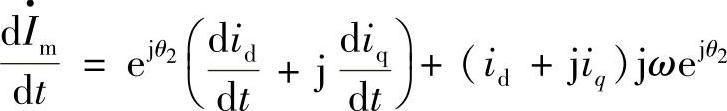
由式（2-63）、式（2-64）可得到空间矢量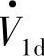、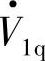为

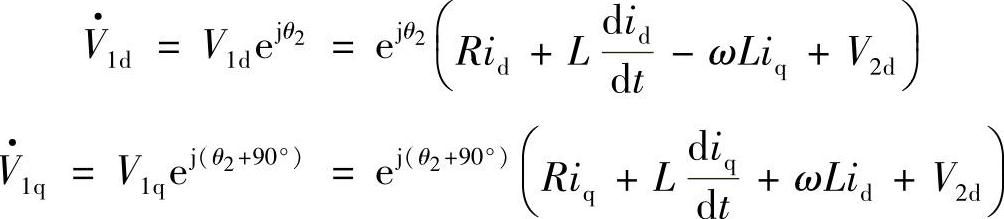
因此，空间矢量电压平衡方程为

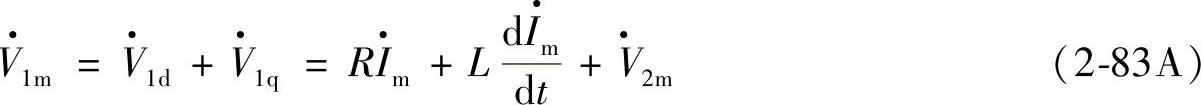
在稳态运行时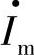，是幅值I_m不变的旋转矢量，此时有

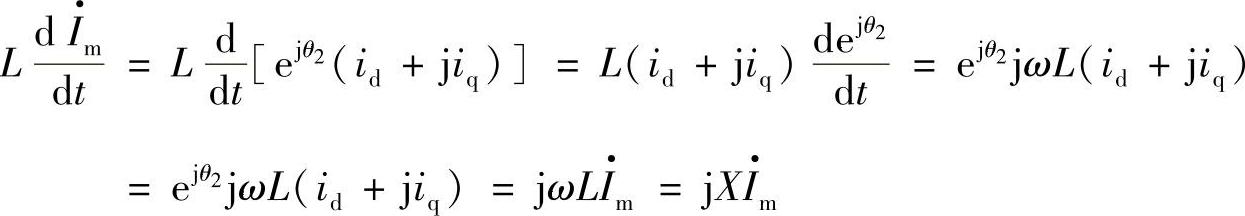
因此稳态时式（2-83A）的电压平衡方程简化为

空间矢量方程式（2-83A）在稳态时简化为式（2-83B），图2-20d变为图2-20e。

式（2-83B）与三相电压、电流对称且处于稳态时的电压时间相量方程类似，但以往相量方程中的电压、电流相量为正弦波有效值，而式（2-83B）中的三相电压、电流是在空间以速度ω随同d、q轴旋转的空间矢量，其幅值为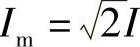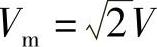，（I、V为相有效值）。因此，采用式（2-59A）经典Park变换（变换阵有2/3因子，稳态时空间矢量大小为正弦波相电压（电流）的幅值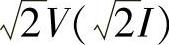，它在A、B、C轴上的投影（分量）当然就是各相电压（电流）瞬时值。