单相桥逆变电路正弦脉宽调制（SPWM）

逆变器理想的输出电压是如图2-16b所示的正弦波v（t）=V_1m sinωt。将图2-16b所示正弦波半个周期π均分p个相等的时区，图中p=6，每个时区的时间T_S=T/（2×6）对应的时区宽度为θ_S=ωT_S=2πfT_S=2π/12=π/6（30°），第k个时区T_S的终点时间为kT_S，起点时间（k-1）T_S，第k个时区的中心点相位角α_k为

α_k=ωt_k=ω（kT_S-T_S/2） （2-37）

图2-16b中当时区数p很大时，正弦波v（t）=V_1msinωt可以看作是由正、负半波各有p个等宽（θ_S=π/p）但不等高（高度为V_1msinωt）的不连续脉波电压①、②、③…组成。图2-16a中逆变电路的输入电压是直流电压V_D，依靠开关管的通、断状态变换，逆变电路只能直接输出三种电压值+V_D、0、-V_D。对单相桥逆变器4个开关管进行实时、适式的通、断控制，可以得到图2-16c所示在半个周期中有多个脉波电压的交流电压v_ab（t）。图中正、负半周（π）范围也被分为p个（p=6）相等的时区，每个时区宽度为π/p=π/6=30°，每个时区有一个幅值为V_D、宽度为θ_k的电压脉波，相邻两脉波电压中点之间的距离相等（π/p=π/6=30°），6个脉波电压的高度都是V_D，但宽度不同，宽度分别为θ₁、θ₂、θ₃、θ₄（=θ₃）、θ₅（=θ₂）、θ₆（=θ₁）。如果要求图2-16c中任何一个时间段T_S中的脉宽为θ_k、幅值为V_D的矩形脉冲电压v_ab（t）等效于图2-16b中该时间段T_S中正弦电压v（t）=V_1msinωt，首要的条件应该是在该时间段T_S中，两者电压对时间的积分值（即电压和时间乘积所相当的面积）相等，即

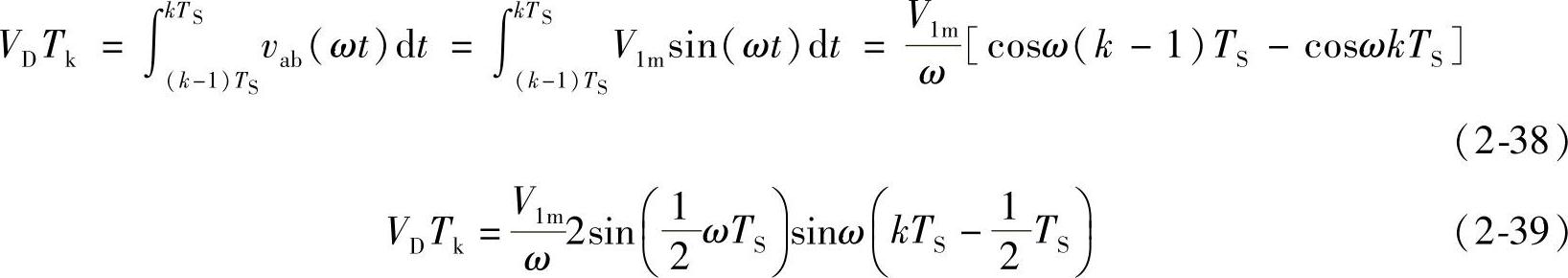
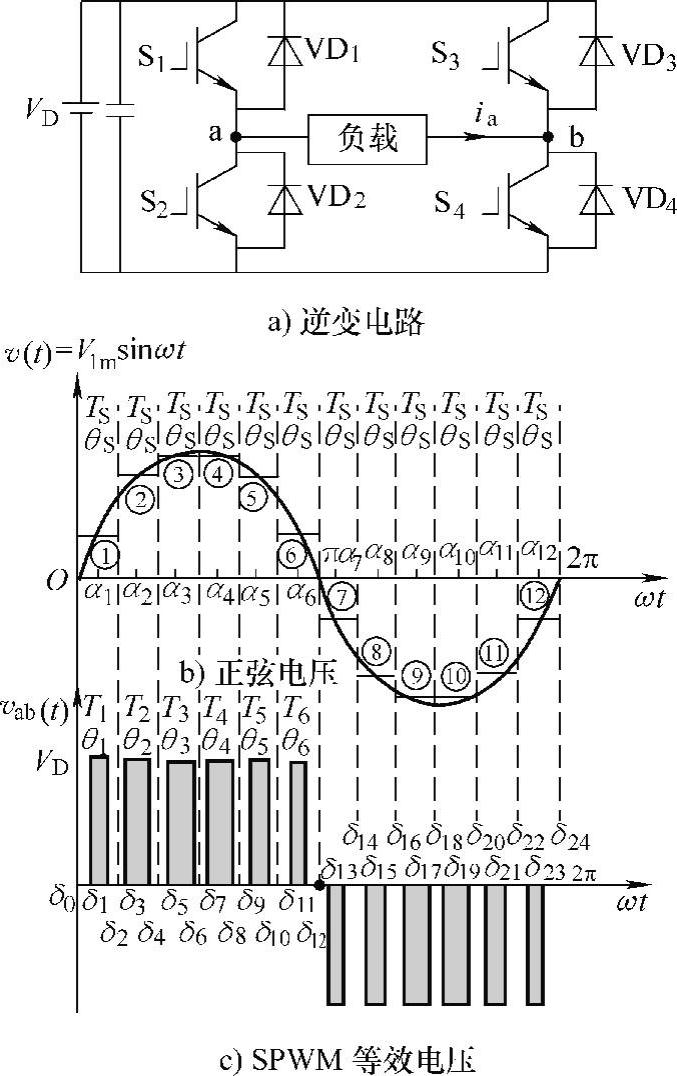
图2-16 用SPWM电压等效正弦电压

由图2-16c可知，式（2-39）左边为第k个逆变电压脉波的积分值，其电压幅值为V_D、作用时间为T_k，对应的脉波电压宽度θ_k=ωT_k，T_k=θ_k/ω；式（2-39）右边式中的ω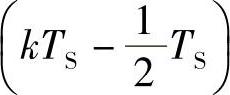是式（2-37）的α_k，即第k个时区中心点的相位角α_k。因此，由式（2-39）可得到

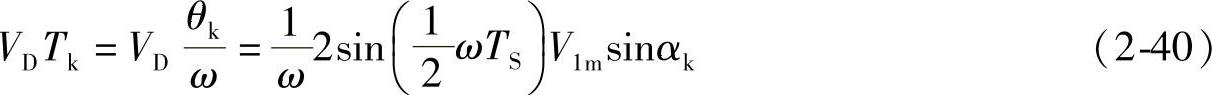
如果半个周期T/2中脉波数p很多，即T_S<<T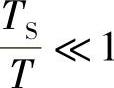，，则有

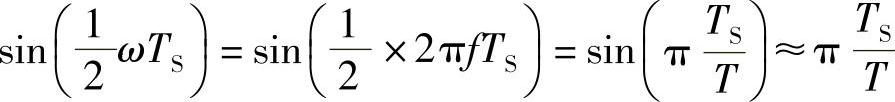
则式（2-40）为

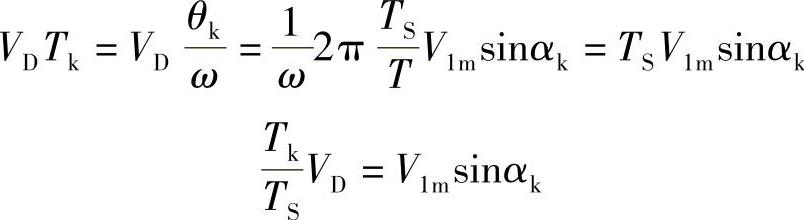
因此，图2-16c中第k个脉波在时间段T_S中电压平均值为

或第k个脉波电压的占空比为

由图2-16b和c可知，在每个脉波电压周期T_S中，逆变器输出一个等高（V_D）但宽度θ_k不同的脉波电压。式（2-41）左边是宽度为θ_k=ωT_k（存在时间为T_k）、高度为V_D脉波电压在周期T_S（宽度为θ_S=ωT_S）中的电压平均值，式（2-41）右边是该脉波周期T_S中，脉波中心点位置角α_k处正弦电压V_1m sinωt的瞬时值，即V_1msinα_k。因此，在任何一个脉波周期T_S中，只要等幅（V_D）不等宽（θ_k）的脉波电压的平均值等于该脉波中心点（α_k）处正弦电压的瞬时值，则等幅不等宽的脉波电压就与该脉波周期T_S中的正弦电压等效。换句话说，只要对逆变电路的开关器件进行实时、适式的通断控制，使每个脉波的平均电压、脉波宽度或占空比按式（2-41）、式（2-42）的正弦规律变化，则逆变电路输出的多脉波电压就能与正弦电压等效。

采样控制理论有一个重要的原理——冲量等效原理：大小、波形不相同的窄脉冲变量（例如电压v（t））作用于惯性系统（例如LR电路）时，只要它们的冲量（即变量对时间的积分）相等，其作用效果相同。大小、波形不同的两个窄脉冲电压（如图2-16b在某一时间段T_S的正弦电压与图2-16c中同一时间段的等幅不等宽的脉冲电压）作用于LR电路时，只要两个窄脉冲电压的冲量相等，则它们所形成的电流响应就相同。因此要使图2-16c的PWM电压波在每一时间段都与该时段中正弦电压等效，除每一时间段的面积相等外，每个时间段的电压脉冲还必须很窄，这就要求脉波数量p很多。脉波数越多，不连续的按正弦规律改变宽度而幅值相同的多脉波电压v_ab（t）就越等效于连续的正弦电压。详细的分析结论是：对开关器件的通、断状态进行实时、适式的控制，使多脉波的矩形脉冲电压宽度按正弦规律变化时，通过傅里叶分析可以得知，输出电压中除基波外仅含有与开关频率倍数相对应的某些高次谐波而消除了许多低次谐波。开关频率越高，脉波数越多，就能消除更多的低次谐波，使逆变电路的输出电压v_ab（t）更近似于连续的正弦波。

如果按同一比例的正弦规律改变图2-16c中所有矩形脉波的宽度θ，则可成比例地调控输出电压中的基波电压数值。这种控制逆变器输出电压大小及波形的方法被称为正弦脉宽调制（SPWM）。

各种PWM控制策略，特别是SPWM控制已在逆变技术中得到了广泛应用。在DC-DC、AC_-DC、AC-AC变换中，PWM控制技术也是一种很好的控制方案并已得到广泛的应用。

在单相桥式逆变电路图2-17a中，四个开关器件S₁～S₄的驱动信号V_G1、V_G2、V_G3、V_G4由图2-17b生成。图2-17b中A、B为比较器，-1为反相器。V_A=-V_A，V_B=-V_B。S₁、S₂的驱动信号V_G1、V_G2由正弦波v_r和三角波v_c的瞬时值相比较确定；S₃、S₄的驱动信号V_G3、V_G4由瞬时值v_r、v_c之和v_r+v_c的正、负值确定。图2-17c画出了正弦波v_r和三角波电压v_c，其中v_r=V_rmsinωt=V_rmsin2πf_rt=V_rmsin（2πt/T_r），被称为正弦参考电压，其幅值为V_rm，频率f_r=1/T_r，T_r为其周期；三角波v_c被称为高频三角载波，其最大值为±V_cm，频率为f_c。三角波与正弦波频率比值称为载波比N=f_c/f_r（图中N=6），正弦波幅值与三角波幅值之比值称为调制比M=V_rm/V_cm（V_rm≤V_cm，M≤1）。由图2-17b可知，v_r、v_c的瞬时值决定了4个开关管的驱动信号及其通、断状态。

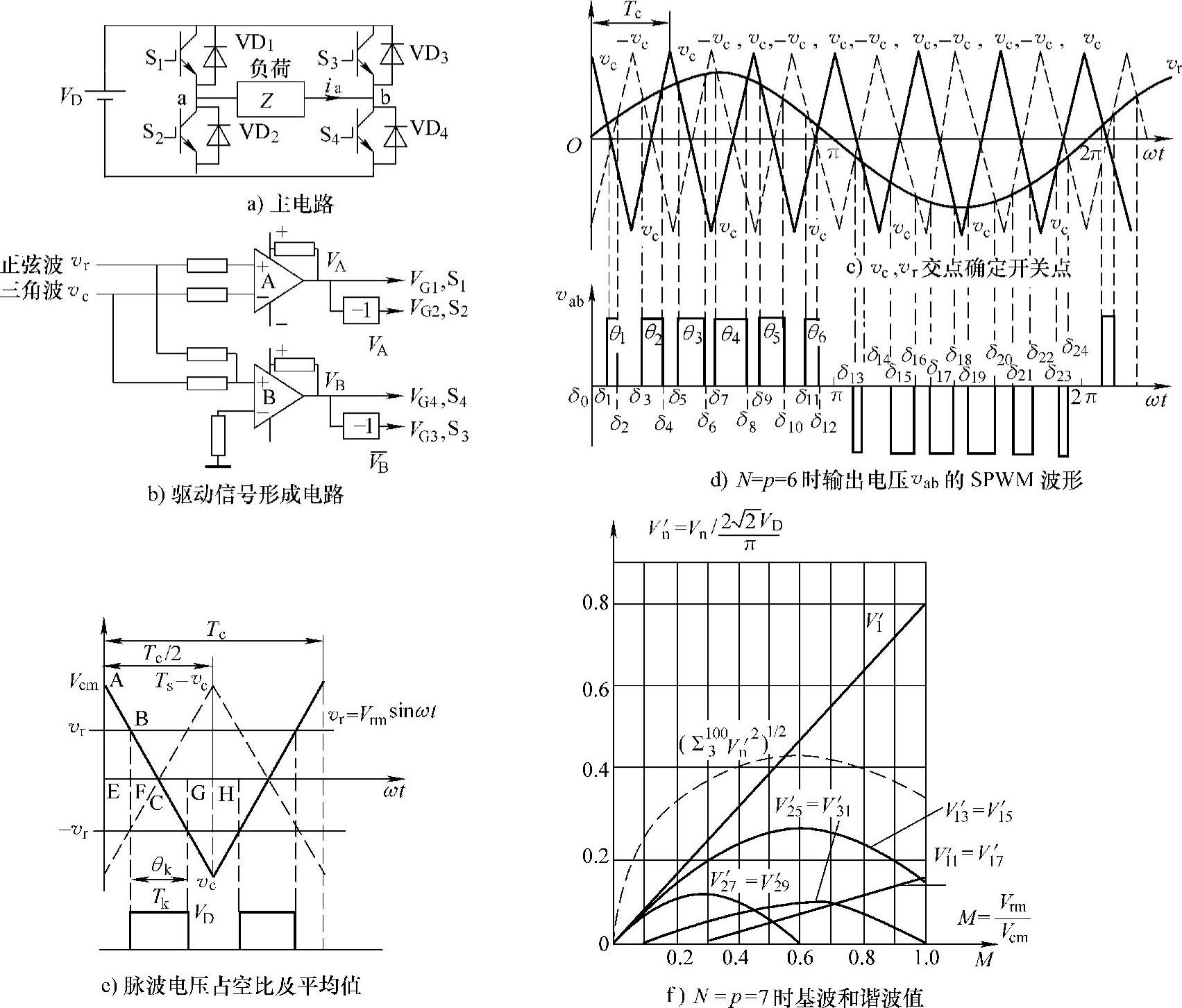
图2-17 单极倍频正弦脉宽调制原理及输出波形

当v_r>v_c时，比较器A输出V_A为正值，S₁被驱动处于通态；V_A=-V_A为负值，S₂截止。

当v_r<v_c时，比较器A输出V_A为负值，S₁截止；V_A=-V_A为正值，S₂被驱动处于通态。

当v_r+v_c>0时，比较器B输出V_B为正值，S₄被驱动处于通态；V_B=-V_B为负值，S₃截止。

当v_r+v_c<0时，比较器B输出V_B为负值，S₄截止；V_B=-V_B为正值，S₃被驱动处于通态。

当S₁、S₄被同时驱动处于通态时，v_ab=+V_D；S₂、S₃被同时驱动时，v_ab=-V_D；当S₁、S3被同时驱动或S₂、S₄被同时驱动时，v_ab=0。

根据图2-17c所示v_c、v_r波形及图2-17b形成的驱动信号可画出在正弦参考电压v_r一个周期T_r期间，从ωt=δ₀=0到ωt=δ₂₄共24个时间段中4个开关管的通断状态及逆变器输出电压波形，如图2-17d所示。

由图2-17c和d可知，逆变电路输出电压v_ab是一个多脉波、对称的交流电压，其基波周期T就是正弦参考波v_r的周期T_r，因此逆变电路输出电压的频率f=f_r，同时v_ab的起始相位角也就是正弦参考电压v_r的起始相位角。此外，改变调制比M（V_rm/V_cm），例如固定三角波幅值V_cm改变正弦波幅值V_rm，将使各脉波宽度同时成比例改变，从而改变输出电压的大小，因此逆变器输出电压的大小、频率和相位（基波正弦电压的起始相位）都可由正弦参考电压v_r=V_rmsinωt控制。

在图2-17c和d中，v_c是正、负对称的三角波电压，在一个三角波周期T_c区域中，形成两个等高（V_D）但宽度θ稍有不同的脉波，脉波周期T_S（对应的相位角宽度θ_S=ωT_S）为T_c/2。载波比N=f_c/f_r=6，v_r、v_c的交点确定了在正（或负）半个周期T_r/2中各有p=N=6个等高的正（或负）单极性脉波电压。

若第k个脉波电压的宽度相角为θ_k，θ_k所对应的时间为T_k，则θ_k=ωT_k，每个脉波的时区时间为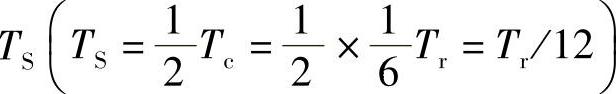，T_S对应的时区宽度相角θ_S=ωT_S=2πf_rT_S=2πT_S/T_r=π/6。由于波形的对称性，6个脉波电压的宽度相角分别是θ₁、θ₂、θ₃、θ₄=θ₃、θ₅=θ₂、θ₆=θ₁。对应的脉波电压V_D存在的时间分别是T₁、T₂、T₃、T₄=T₃、T₅=T₂、T₆=T₁，若各脉波的中心点相位角为α₁、α₂、α₃、α₄=π-α₃、α₅=π-α₂、α₆=π-α₁，各脉波电压的起始和终止相位角为δ₁、δ₂；δ₃、δ₄；δ₅、δ₆；δ₇、δ₈；δ₉、δ₁₀；δ₁₁、δ₁₂，其中δ₁₂=π-δ₁；δ₁₁=π-δ₂；δ₁₀=π-δ₃；δ₉=π-δ₄；δ₈=π-δ₅；δ₇=π-δ₆，则图2-17d的v_ab是一个半波对称的奇函数，即

v_ab（ωt）=-v_ab（ωt+π）=-v_ab（-ωt）

由傅里叶级数分析可知：(www.xing528.com)

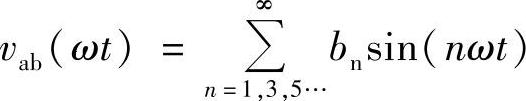
式中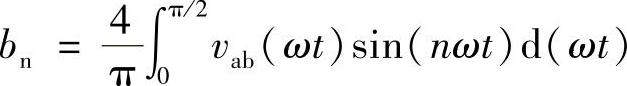，n=1，3，5…

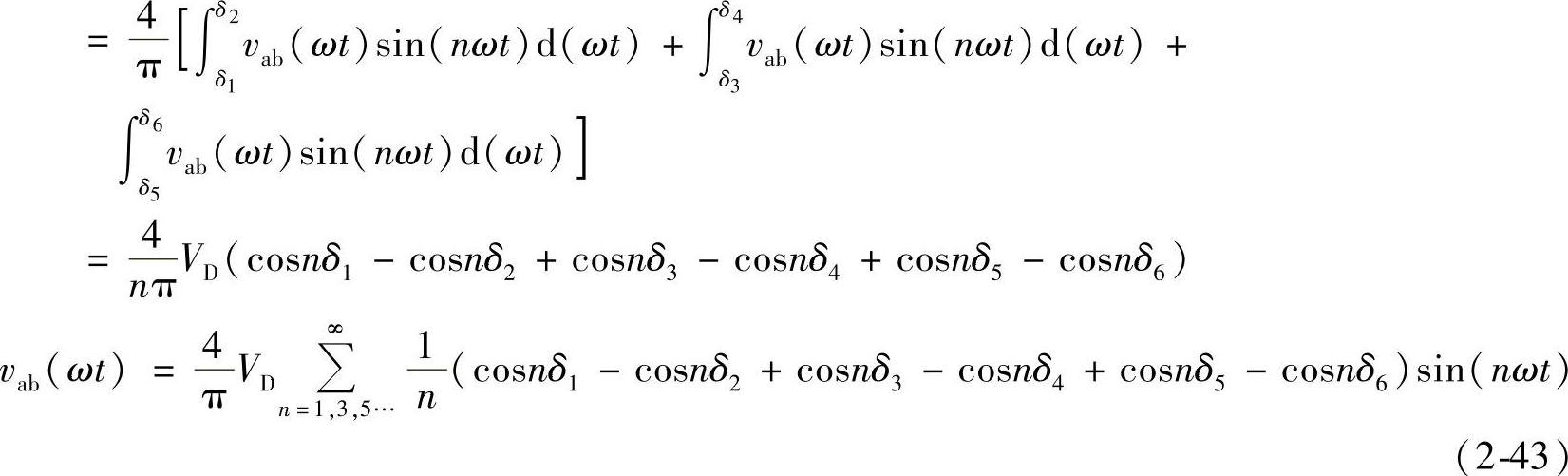
n次谐波有效值为

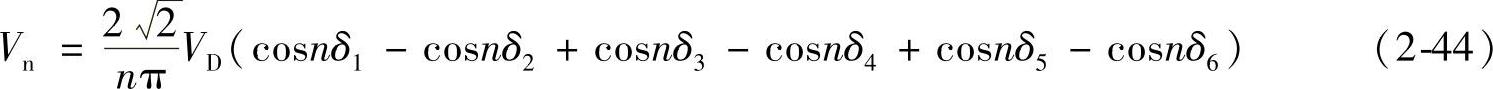
基波电压有效值为

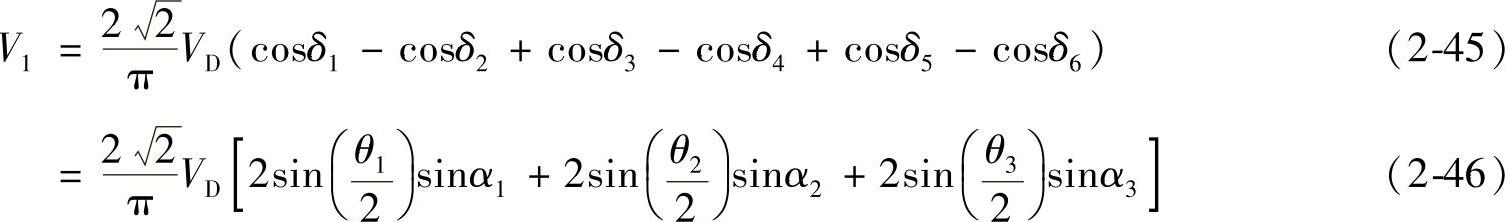
图2-17c中，每半个载波周期T_c/2中，有一个脉波电压（脉宽θ_k存在的时间为T_k，θ_k=ωT_k），即脉波周期T_S=T_c/2，图2-17e画出了一个脉波周期T_S中的脉波电压。由于脉波数p很多，脉波周期T_S很小，在一个T_S中正弦参考电压v_r=V_rm sinωt变化很小。若脉波中心点的相位角为α_k，则在这个脉波周期T_S中可以认为v_r=V_rmsinα_k不变。图2-17e中，在一个脉波周期T_S中，即ωt在EFCGH区间：当ωt在EF区间，v_r<v_c，v_r+v_c>0，S₂、S₄处于通态，v_ab=0；ωt在FG区间，v_r>v_c，v_r+v_c>0，S₁、S₄处于通态，v_ab=+V_D；ωt在GH区间，v_r>v_c，v_r+v_c<0，S₁、S₃处于通态，v_ab=0。因此在一个脉波周期T_S（或θ_S=ωT_S）期间，脉波电压宽度θ_k=ωT_k，脉波电压在该脉波周期T_S中的平均值为

由图2-17e中三角形AEC的简单几何关系得到

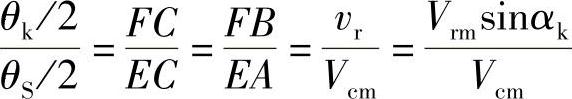
因此，第k个脉波电压的平均值为

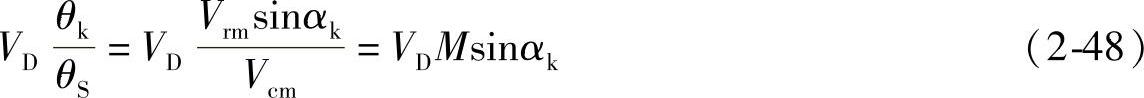
第k个脉波电压的占空比为

SPWM控制时，若载波比N=f_c/f_r很大，输出电压半个周波（T/2）中的脉波数p很多，即T_S<<T时，逆变电路输出电压将是很多个宽度很窄的不连续脉波电压的集合，脉波电压在一个很短周期T_S中的平均值可看作是该周期T_S中α_t=ωt的瞬时值，即认为第k个脉波的占空比D_k（θ_k/θ_S，α_k=ωt）就是在t瞬间、相位为α_t=ωt时的占空比D_t，即

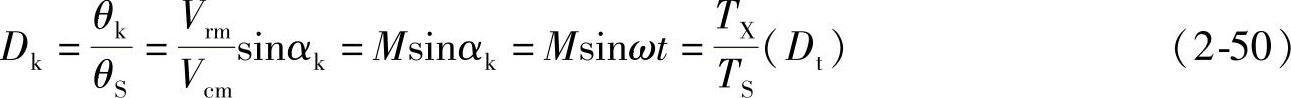
由此可得到逆变电路采用SPWM时，其输出电压瞬时值为

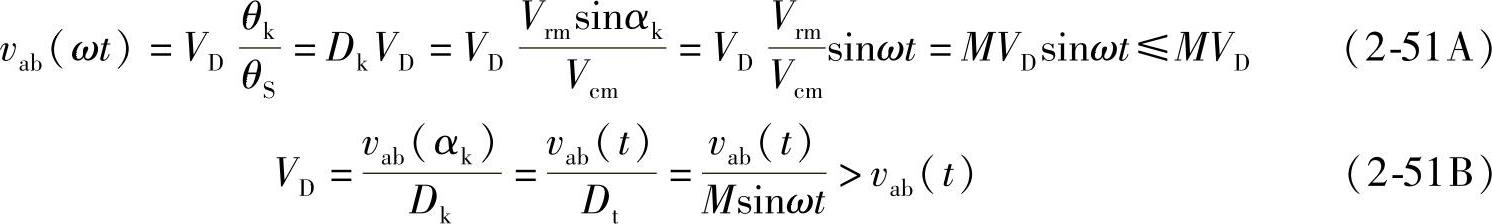
调制比M≤1，因此采用SPWM控制时输出的交流电压总是小于直流电压V_D。SPWM逆变，就电压变换而言，本质上类似于2.4.1节的DC-DC降压变换，只是占空比D在交流电压一个周期中按正弦规律变化。

采用SPWM控制时，逆变器输出电压的基波幅值为

基波电压的有效值为 V₁=MV_D/2=0.707MV_D （2-53）

改变调制比M，例如固定三角波幅值V_cm但改变正弦参考波幅值V_rm，即可调控输出基波电压值。SPWM控制要求V_rm≤V_cm，调制比M=V_rm/V_cm≤1，因此SPWM控制的单相逆变电路输出的最大电压幅值为V_D，最大的有效值为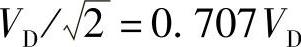。它比120°脉宽的单脉波电压有效值0.78V_D还要小。由式（2-51）还可看出输出电压的频率、相位就是正弦参考电压v_r的频率和相位，所以逆变器输出电压的数值、频率和相位可由正弦参考电压的幅值、频率和相位调控。

前面已经论述，如果要求逆变电路输出的恒幅（V_D）不等宽度θ_k的多脉波电压与正弦电压V_1msinωt等效，脉波数p或载波比N=f_c/f_r必须很大，且各脉波电压的宽度θ_k或占空比D_k应按式（2-42）确定。采用图2-17b中三角波v_c与正弦波v_r的交点确定逆变电路4个开关器件的通断状态时，得到的各脉波电压的占空比D_k、各脉波电压宽度θ_k的公式（2-50）正好就是式（2-42），即各脉波电压的宽度θ_k、占空比D_k与该脉波中心点处相位角α_k的正弦函数成正比，或脉波电压的平均值等于正弦电压在中心点α_k处的瞬时值。

图2-17d所示波形特点是输出电压的正半周中只有正值脉波电压+V_D，负半周中只有负值脉波电压-V_D，这种脉波电压被称为单极性脉波电压。此外，在每个载波周期T_c中形成有两个脉波电压。如图2-17c中正、负半波各有3个载波周期T_c，但正、负半波中各有6个单极性脉波电压，即载波比N=f_c/f_r=6时，一个输出电压周期T（2π）中共有2×6=12个正、负脉波，即正、负脉波数2p=2×6=12，比载波比N=6高一倍，故称这种SPWM控制方式为单极性倍频SPWM控制。

已知正弦参考波电压v_r=V_rmsinωt和三角波频率f_c、幅值V_cm后，可以确定图2-17c中v_r、v_c、-vc的电压交点，即确定各脉波电压的起始和终止角δ₁、δ₂、δ₃、δ₄、δ₅、δ₆以及各脉波宽度θ₁=δ₂-δ₁、θ₂=δ₄-δ₃、θ₃=δ₆-δ₅，可以确定各脉波中心点位置角α₁=（δ₁+δ₂）/2、α₂=（δ₃+δ₄）/2、α₃=（δ₅+δ₆）/2，利用式（2-46）或式（2-44）即可计算出基波和各次谐波有效值V₁、V_n。图2-17f画出了载波比N=7，每半周中有p=N=7个脉波，不同调制比M=V_rm/V_cm时，基波和谐波电压的相对值（取基准值为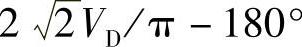单脉波时的基波有效值）的计算结果。当调制比M=V_rm/V_cm≤1时，逆变器输出电压v_ab中的基波电压有效值V₁与调制比M成正比，M=1时，由式（2-53）得。

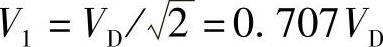如果输出电压半个周期T/2中，有p个单极性电压脉波，深入分析这种单极性SPWM控制的输出电压波形得知：除基波外，v_ab（t）还含有一系列高次谐波（即2p±1、2p±3，4p±1、4p±3等阶次的谐波），其中幅值较大而阶次又较低的高次谐波阶次为2p±1次。图2-17f示出了p=N=7时的基波和谐波的相对值，由于p=N=7，故幅值较大高阶次又较低的高次谐波为2p±1=2×7±1=13、15次。

将SPWM波的基波和谐波与180°宽单个矩形波的基波和谐波相比较可知：

1）采用单极性SPWM控制后，幅值较大而阶次又较低的谐波为2p（p=N）-1次谐波。

2）采用SPWM控制后，基波最大的有效值V₁（在M=V_rm/V_cm=1时）为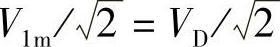=0.707V_D，它与180°矩形波的基波有效值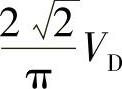=0.9V_D的比值为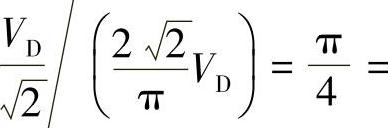0.7854。因此采用SPWM控制在消除低次谐波、改善输出波形的同时使输出电压（即直流电压利用率）减小了21.46%。

3）采用SPWM控制后尚存的某个频率的高次谐波数值比180°宽的矩形波可能还大些。例如180°宽矩形波中11次谐波为基波的1/11，即9%。而在SPWM控制时，图2-17f中，11次谐波还大于基波的9%，但这不会带来严重的后果。因为11的二次方是121，经LC滤波后，其在负载端11次谐波要衰减11的二次方倍即121倍，因此负载端的电压畸变率还是很小的。