无线电阻时输电系统的功率-电压特性

如果忽略线路电阻，R=0，tanφ=X/R无限大，则可使式（1-38）～式（1-42），Q_∗-V_∗特性和P_∗-V_∗特性大为简化，致使传输功率P_∗、Q_∗和线路电抗等参数影响电压V∗的一些物理概念更清晰。当R=0，tanφ=X/R=∞时，由式（1-37）可得到

V⁴∗+（2Q∗-1）V²∗+P²∗+Q²∗=0 （1-43）

由（1-43）式得到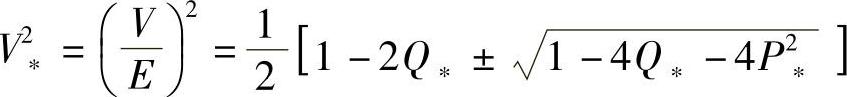　（1-44）

由（1-43）式也可得到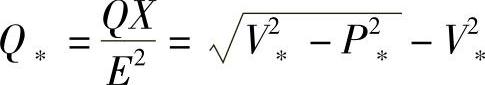 （1-45）

由（1-45）式得到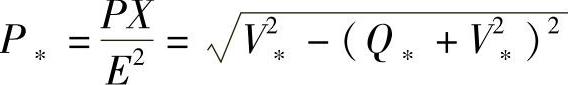 （1-46）

1）对于一定的有功功率P∗，由式（1-45），令dQ_∗/dV_∗=0，可求得图1-11b中以P∗为参变量的临界电压V_cri∗及其对应的临界滞后无功功率Q_cri∗和临界电动势E_crit的近似值，即

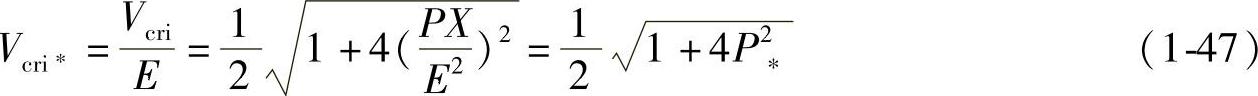
由式（1-45）和式（1-47）又可得

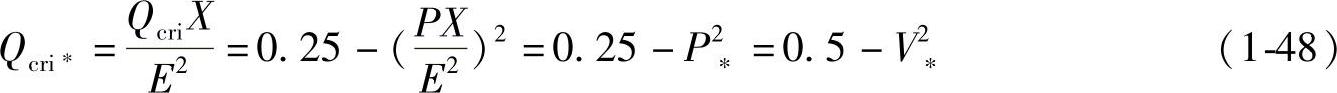
由上式还可得到对应于V_cri∗、Q_cri∗的首端电动势E的临界值，即

当传输有功功率P_∗为定值时，为使电压能稳定运行，必须使V_∗>V_cri∗，同时Q∗<Q_cri∗，由式（1-47）和式（1-48）可得到

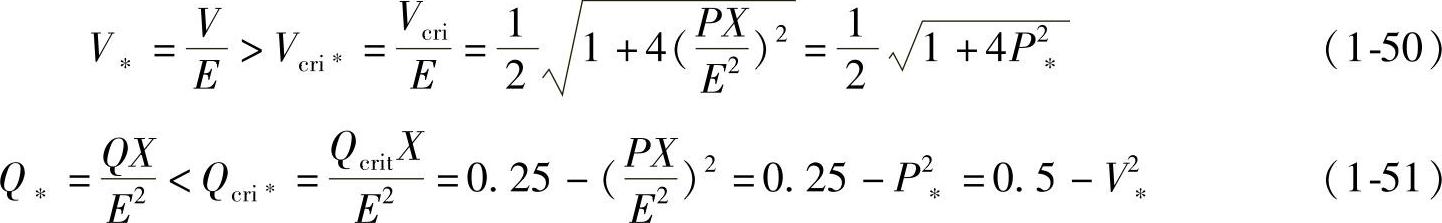(www.xing528.com)

由式（1-50）可知：传输的有功功率P越大，输电线电抗X越大，电源电动势E越小，要电压稳定运行必需的临界电压V_cri值越高，同时由式（1-48）可知线路能传输的感性无功功率Q_∗也应越小。由式（1-51）可知，当P∗、X较大，E不够大时，Q_∗<0，即在负荷节点处必须有感性无功功率源，才能使线路传输有功功率P∗时能维持节点电压的运行稳定性。

2）对于一定的无功功率Q∗，由式（1-46），令dP_∗/dV_∗=0，可求得图1-11d中以Q_∗为参变量的临界电压V′_cri及其对应的临界有功功率P′_cri∗，即

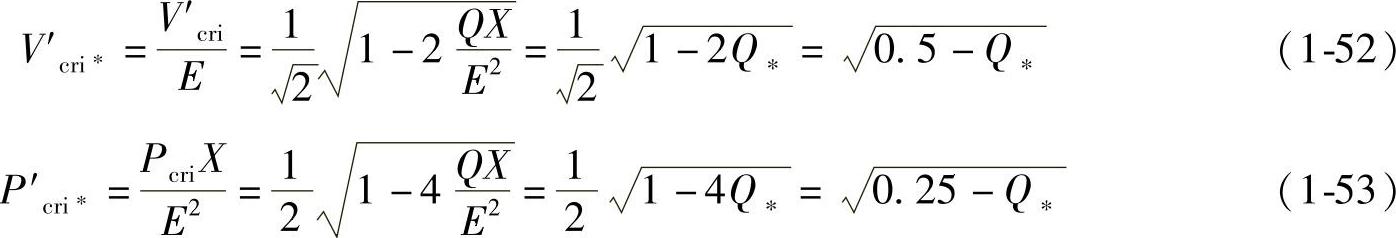
由式（1-53）也可求得这时的临界电动势，即

当传输的无功功率Q∗为恒定值时，电压稳定运行的条件是V_∗>V′_cri∗，同时P_∗<P′_cri∗，由式（1-52）、式（1-53）得到

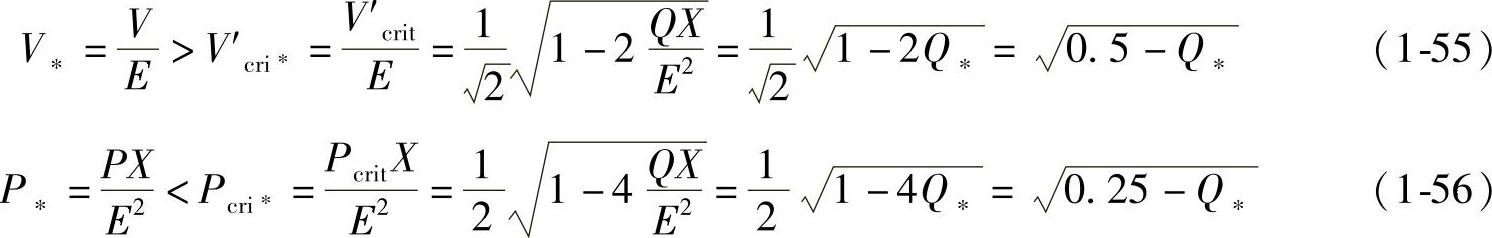
传输的感性无功功率Q越大、输电线电抗X越大、电源电动势E越小时，则负载节点电压越低，同时能够传输的临界有功功率P_cri∗也越小。由式（1-56）还可看到，当Q、X较大，E又不大时，P_∗可能为零，这时电源E根本不可能经电抗X向末端节点传输有功功率P，在负载节点处必须有一定的感性无功功率电源才能使线路传输有功功率并维持节点电压运行的稳定性。

电网中某一节点电压的临界值V_cri∗，是由连接到该节点的负载和连接到该节点的系统等效电抗X共同确定的。P、Q、X越大，则确保电压稳定所需的电源电动势E也应越高。因此远距离重载输电且传输较大无功功率时，易于失去电压稳定性，而且电网中不同节点、不同运行工况时有不同的供电点电压临界值。从安全可靠运行出发，电力系统当然不能在临界电压附近运行，应使系统节点电压高于临界电压并保证有一定的稳定裕度，表示稳定裕度的电压储备系数定义为

式中，V₀为电力系统在一定的运行工况时某节点的实际最低电压；V_crit为该节点在该运行工况时的临界电压。正常运行时，通常要求K>10%～15%；在事故后运行和特殊运行方式下，通常要求K>5%～8%。

线路传输功率（特别是无功功率Q）越大，线路电抗X越大，首端电源电压E越低，则负载节点电压V越低。实际电力系统运行中，负载（特别是感性负载）的突增，或则双回路输电线路跳开一回路，使线路电抗增倍，并且/或则由于电源电压E降低到一定程度，都可能使电压降到接近电压临界稳定值V_crit，电压的下降使无功功率不平衡程度更严重，恶性发展将引起电力系统电压崩溃，导致大面积停电事故，造成重大经济损失和社会影响。1973年7月中国大连，1978年12月法国，1983年瑞典，1987年7月东京，1996年7月2日和8月10日美国西部，2003年8月北美等大停电事故都与系统电压崩溃有关。因此在电力系统中采用电力电子技术、补偿和控制无功功率，对电力系统的安全运行也具有重大意义。