线路电阻对输电系统的功率-电压特性的影响

在图1-11a中，电动势E经过等效阻抗Z（含发电机阻抗、线路阻抗及变压器阻抗等）向末端负载供电。如果负载所需的无功功率为Q_L，发电机的电动势E经过电抗X输送到末端的无功功率Q_∗等于Q_L，若这时末端电压等于额定值（或在指令值的范围内），我们称这时的运行的工况是无功功率平衡。由于电力系统中的电压降落主要是传输无功功率、无功电流流过电抗引起的，因此当E一定时，如果负载所需的无功功率过大，虽然系统供给的无功功率Q_∗仍然等于Q_L，但若这时电压V达不到额定值（或偏差超过指令值范围），我们称这种工况为无功功率不平衡，因此电力系统中节点电压水平是电力系统中无功功率供需平衡情况的具体体现。在一定的指令电压下，线路能提供的无功功率Q_∗低于该指令电压时负载的无功功率Q_L，即Q_∗<Q_L，此时称为系统无功不足，将使V_下降，V低于指令电压。反之Q_∗>Q_L时，称为系统无功过剩，将使电压V上升，高于指令电压。

在实际的电力系统中，传输无功功率不仅会产生很大的无功和有功损耗，而且过大的电压降落会导致电网电压过低，引发电力系统的电压崩溃。电力系统中同一节点不同时刻无功功率供需平衡情况可能不同，不同节点同一时刻无功功率供需平衡情况也不尽相同。系统中各点的电压调节主要应靠就地无功功率的供需平衡调节实现。而不同节点间的无功供需相互支援和调节往往受到许多条件的限制，特别是相距较远的或电气距离（节点间的等效电抗）较远的各节点更是如此。

图1-11a所示的输电系统中，若线路（含折算后的变压器）等效阻抗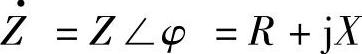，R=Zcosφ，X=Zsinφ，负载等效阻抗Z·_L=Z_L∠φ_L=Z_L cosφ_L+jZ_L sinφ_L=R_L+jX_L，R_L=Z_L cosφ_L，X_L=Z_L sinφ_L（φ_L为负载功率因数角）。取电压V相位为零，电动势E·超前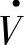的功率角为δ，则V·=V∠0°=V，E·=E∠δ=Ecosδ+jEsinδ。若线路电流I·的共轭相量为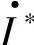，则线路传输给末端负载的功率为

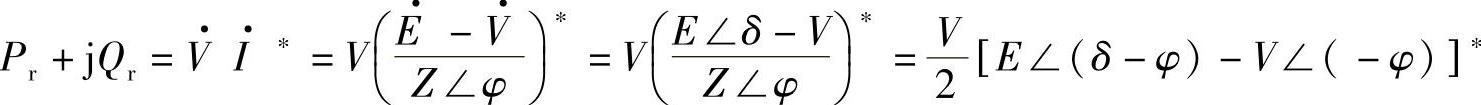
由上式也可得到1.2节中P_r、Q_r的公式。

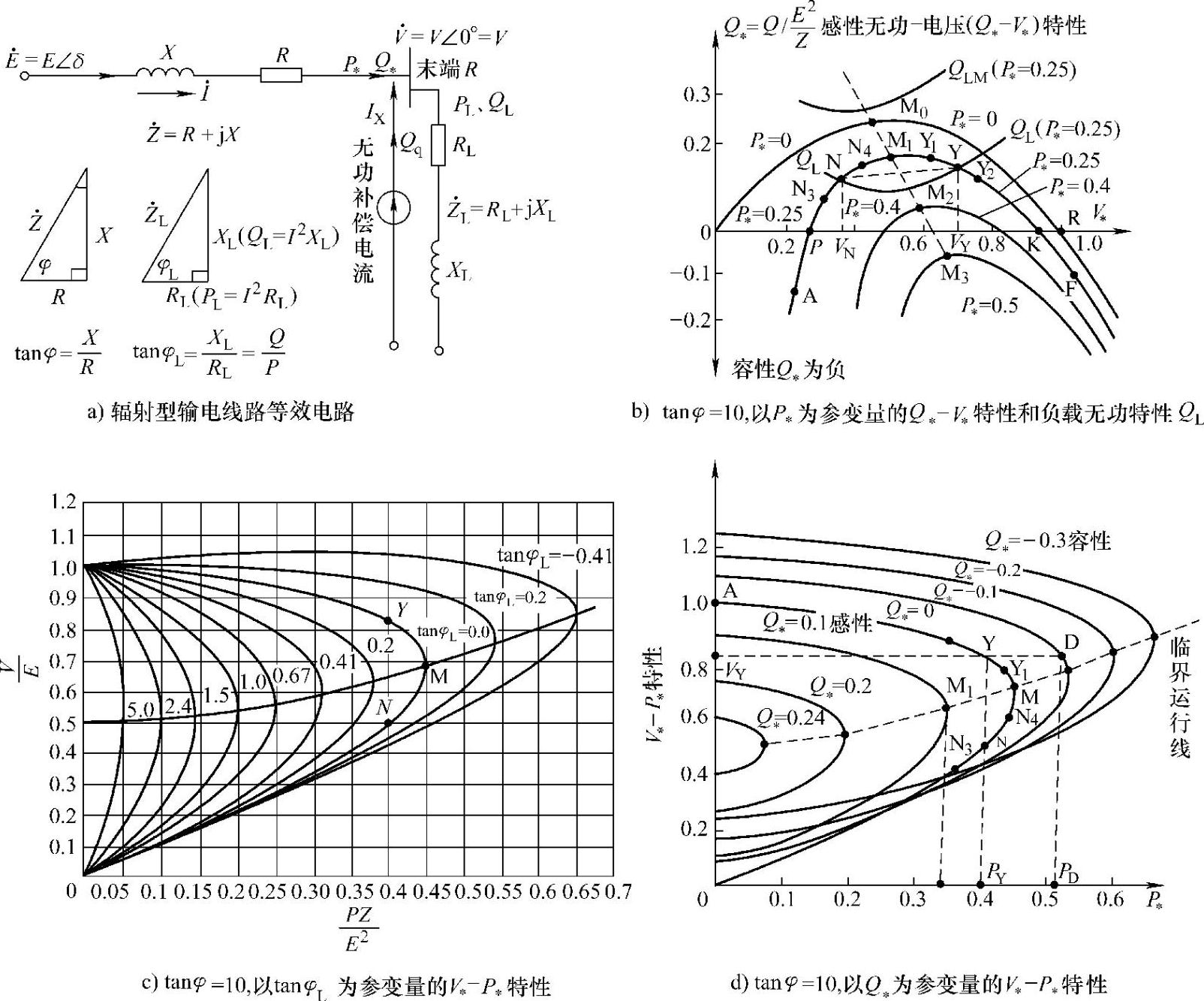
图1-11 有功功率、无功功率-电压特性

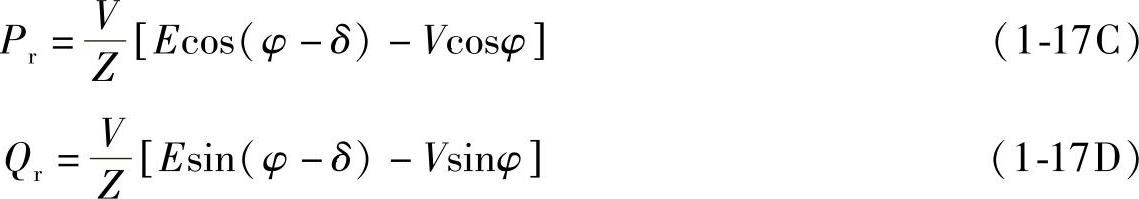
忽略线路电阻，即R=0、φ=90°时，有

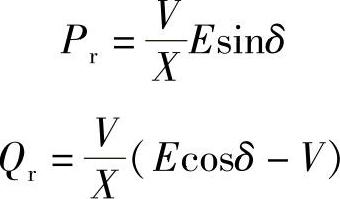
取电压V的基准值为E，功率的基准值为E²/Z，则V的标幺值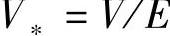，功率的标幺值P∗=P_rZ/E²，Q∗=Q_rZ/E²，由式（1-17C）、式（1-17D）可得

P_∗=V_∗cos（φ-δ）-V_∗cosφ （1-35）

Q_∗=V_∗sin（φ-δ）-V_∗sinφ （1-36）

由以上两式消去变量δ，可得到P∗、Q∗、V∗标幺值（无量纲）方程为

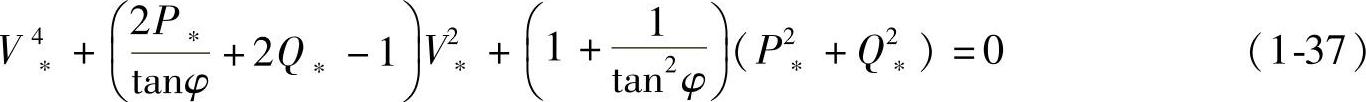
1.无功功率与电压特性

由式（1-37）可得到V∗与P∗、Q∗及tanφ的函数关系：

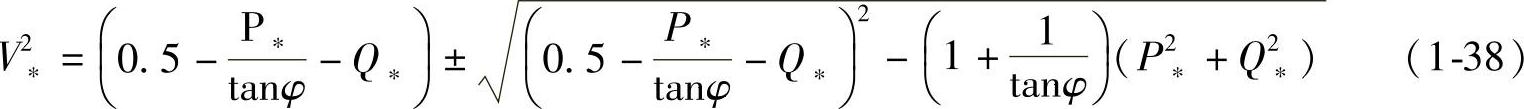(www.xing528.com)

由式（1-37）也可得到Q∗与V∗、P∗以及tanφ的函数关系为

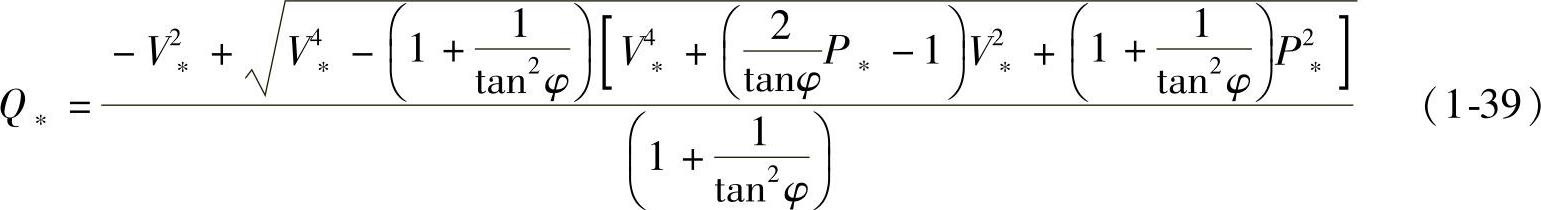
式（1-39）表明，线路能传送至末端负载的无功功率Q∗与P∗、V∗及tanφ（X/R）有关。对于一个给定的线路阻抗参数tanφ（X/R），以P_∗为参变量，式（1-39）的Q_∗=f（V∗，P∗，tanφ）称为无功-电压（Q-V）特性。图1-11b给出了tanφ=X/R=10，参变量P_∗=0、0.25、0.4、0.5时的Q-V特性。图中，P_∗=0的Q-V曲线是线路仅传输无功时的Q、V函数关系。Q_∗=0时线路空负荷，在空负荷R点，V∗=V/E=1.0，即V=E。从空负荷点R开始，感性无功功率Q_∗从零增大时，V_∗下降，到达M₀点，Q_∗达到最大值，此后V_∗继续减小时，线路能提供给负载的感性无功功率Q_∗反而减小，M₀点被称为临界点，M₀点的电压、功率被称为临界电压V_crit、临界功率Q_crit。

对比图1-11b中P∗=0和P∗=0.25、P∗=0.4等几个Q-V特性关系可知，线路传输的有功功率P∗越大时，线路能传输的感性无功功率越小，临界电压V_cri∗越高。图1-11b中P∗=0.25的Q-V特性曲线表明：当传输有功功率P∗=0.25时，在Q∗=0的K点时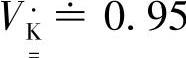，。若传输无功功率Q∗（感性）>0，则V∗<V_K；若传输无功功率Q∗<0（F点容性无功功率），则V∗>V_K，感性无功功率Q∗从零增大时，V∗从V_K减小，到达临界点M₁时，Q_∗达到最大值Q_crit，V∗=V_M1=V_crit为P∗=0.25时的临界电压。此后V∗继续减小时，线路能提供的Q∗不但不能增大反而下降。超过P点后，Q∗为负值，表明在很低的电压V∗下，必须有容性电流流过线路电抗才能传输P∗=0.25的有功功率。图1-11b中将不同参变量P∗的Q-V曲线的临界点M₀～M₃连接，可得到临界运行线M₀～M₃。图中M点的纵坐标V_M是传输一定有功功率时线路能传送的最大无功功率Q_cri∗，M点的横坐标是对应的电压V_cri∗。图1-11b中的曲线Q_L是线路tanφ=10，传输有功功率P∗=0.25时负载无功功率Q_L与负载电压V∗的特性（参数见图1-10c中的Q_L=Q₁+Q₂）。Q_L与P∗=0.25时的Q_∗-V_∗特性有两个交点N（V_N）、Y（V_Y）。在这两个交点，线路能传输的有功功率P_∗与负载有功功率P_L相平衡（P∗=P_L=0.25），线路传送的无功功率Q∗与负载在相同电压时的无功功率Q_L平衡，Q∗=Q_L，当工作在Y点时，一旦系统受到扰动而使V∗略有上升到Y₂点的V_Y2时，由于电压升高，图1-10c中负载的Q_L将增大，使线路无功电流增大，电压降增大，而使V∗回落。同时由于V_∗上升，输电线路能提供的无功Q_∗又减小，Q_∗<Q_L，系统无功不足，不能维持电压V_∗=V_Y2不变，也使V_Y2回落到V_Y。反之，当扰动使工作点上移至Y₁点时，由于V_Y1<V_Y，负载Q_L减小，线路无功电流减小，电压降减小，又使V_Y1回升，同时由于Y₁点线路能提供的无功Q_Y1>Q_Y，系统无功过剩，也要使V_Y1回升到V_Y。因此，在Y点电压V_Y下工作，系统电压是稳定的。但是在电压V∗较低的N点运行时，稍有扰动使V∗下降到N₃点V_N3时，由于Q_L增大，线路电压损耗加大，使V_∗更下降，又Q_∗<Q_L，致使系统无功不足以维持V∗=V_N3而继续不断下降，致使系统电压崩溃。所以系统能稳定运行的工作点只能是V∗高于临界电压V_cri∗的Y点，要系统电压不发生电压崩溃，必须负载节点电压V∗>V_crit，由图1-11b可见，传输的有功P∗越大，临界电压V_crit越高，确保运行电压不崩溃所必需的运行电压也越高。P_∗越大，Q_cri∗越小，能传输的最大的感性无功Q∗也越小。当P∗大到接近0.5时，为了传输P∗=0.5的有功功率，Q_∗必须为容性无功。

若图1-11b中Q_LM为感性无功负载非常大时的无功-电压特性，则Q_LM与P∗=0时的Q∗没有交点，说明即使线路不传输有功功率也不能向无功负载供电。这时如果在负载节点处设置无功补偿器，向负载节点输出感性无功Q_q补偿过大的Q_LM（参见图1-11a），使线路末端等效无功负载减少到Q_L=Q_LM-Q_q，线路就能传输P_∗、Q_∗了。

2.系统的有功功率-电压特性

由式（1-37）还可得到传输线有功功率P∗与V∗、Q∗的函数关系，即

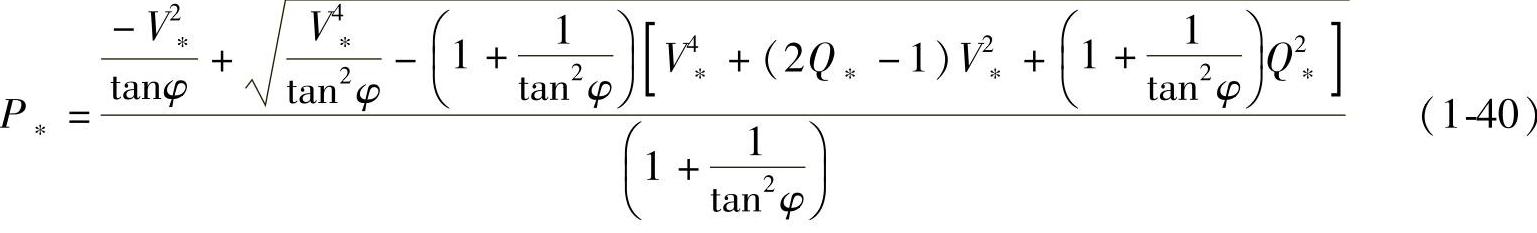
负载功率因数角为φ_L时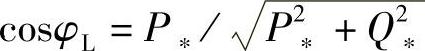，，tanφ_L=Q∗/P∗将Q∗=P∗tanφ_L代入式（1-37）可解得P∗与V∗、tanφ_L的函数关系为

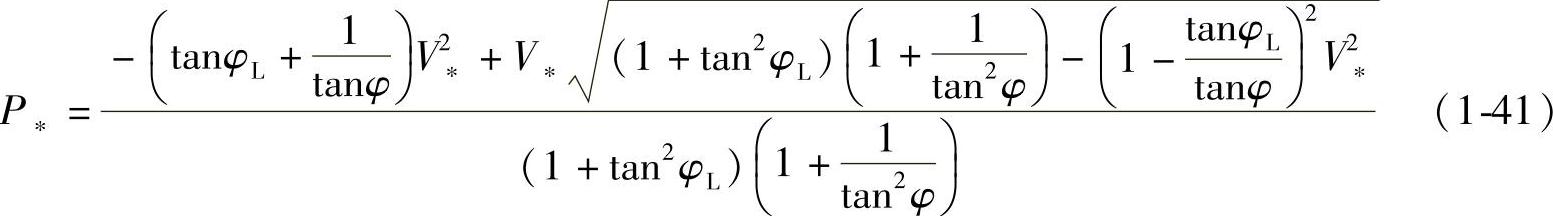
在一定的线路阻抗角φ（tanφ=X/R），式（1-41）表达的电压V∗与有功功率P∗的函数关系被称为V-P特性，例如取tanφ=X/R=10时，以负载功率因数角φ_L（tanφ_L=Q/P）为参变量，如图1-11c和表1-1所示。图1-11c所示曲线俗称鼻形曲线。tanφ_L=0，空负荷、P_∗=0时V∗=1，即V=E。P∗从零增大时，V∗下降，但到达临界点M点，V∗=V_crit（临界值），P∗达到最大值（临界值）P_crit。超过临界点M，V∗继续减小时，P_∗反而从P_cri∗减小，线路传输的有功功率P∗不能超过P_cri∗。tanφ不同时，临界点M的V_crit和P_crit也不同，不同tanφ_L临界点的连接线称为临界运行线。图1-11c中tanφ为负值表示传输容性无功Q∗=tanφ_L·P_∗，tanφ_L为正值表示传输感性无功功率。由式（1-41）令dP∗/dV∗=0，可求得临界电压V_crit和线路能传输的临界（最大）有功功率P_crit。

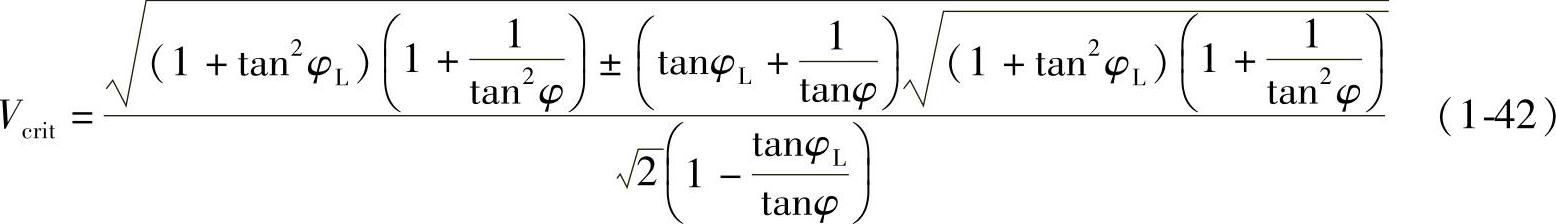
式中，V_crit为图1-11c中的M点的电压，M点所对应的临界有功功率P_cri∗是一定的tanφ（Q/P）线路能传输的最大功率。由图1-11c还可看到线路传输感性无功相对值越大（tanφ_L正值大）时，M点的P_crit、V_crit越小；而传输容性无功（tanφ_L<0，Q∗为负值），则使M点P_crit、V_crit增大。在线路末端设置无功补偿使Q∗为负值，是改善电力系统电压稳定性、提高线路输电能力的有效措施。

表1-1 线路中tanφ=X/R=10，以负载tanφ_L=X_L/R_L为参变量的V-P特性

图1-11d是按式（1-40）画出的tanφ=10，以Q_∗为参变量，传输功率P-V特性曲线。与图1-11c不同的是，不用tanφ_L（Q/P）作参变量而直接用无功功率Q_∗作参变量。由于线路电压损耗主要取决于Q_∗而不是P_∗，直接用Q_∗作参变量分析一定传输功率P_∗、Q_∗时电压V_∗的特性更清晰、直观。在图1-11d中，Q_∗=0的一条V-P特性是仅传输P∗时的V-P特性，A点P_∗=0时，V_∗=1.0，V=E，P_∗从零增大时，V∗下降，到达临界点M后，V∗继续下降，P_∗反而减少，表明线路传送一定的无功功率Q_∗时，线路传输的有功功率不能超过临界M点的有功功率P_cri∗，与之对应的电压是临界电压V_cri∗。