发电机稳定性及极限输电功率

电力系统正常运行时，发电机经常受到不同类型的扰动，破坏其功率平衡。我们把电力系统运行中受到微小的或巨大的扰动之后能否继续保持发电机之间同步运行的问题称为电力系统的稳定问题。电力系统受到的扰动大小不同，其电压、电流、功率、功角δ及转子相对运动速度Δω（dδ/dt）和相对加速度dΔω/dt（d²δ/dt²）等运行参数的变化情况也随之不同。对系统受到微小的扰动和遭受大扰动后的过渡过程，实际采用的分析和计算方法也有所不同。国际电气与电子工程师协会（IEEE）把电力系统稳定问题分为暂态稳定（Transient-state stabili-ty）和静态稳定（Steady-state stability）两大类并给出了相应的定义。

1）暂态稳定（大扰动稳定）：对于一个特定的初始稳定运行状态，以及对于某一特定的扰动（例如输电线短路故障），如果扰动后系统可以达到一个可以接受的新的稳定运行状态，则对此初始状态及对此扰动而言称之为是暂态稳定的。这一定义实际上和大扰动稳定对应，只要求最后达到一个可以接受的新的稳定运行状态。对于不同的初始状态及不同的扰动要分别做不同的大量计算以便确定系统的暂态稳定性。

2）静态稳定（小扰动稳定）：对于某一特定的初始稳定运行状态，电力系统遭受一个微小的扰动（理论上扰动量趋近于零），系统经历一个过渡过程后，趋于恢复扰动前的运行工况，则称系统在此特定的运行工况下具有小干扰稳定性。如果对系统在小干扰下的动态行为进行分析时，首先将描述系统动态行为的非线性微分方程组在运行工作点线性化，化为线性化微分方程组，然后用线性化理论及相应的方法（如特征根分析、扫描分析等）进行分析，系统模型计及系统元件和调节控制器的动态特性，从而实现严格的小干扰稳定性分析。工程上则称之为动态稳定分析。但是通常在实际小扰动稳定分析时，常对线性化微分方程作进一步简化，即忽略系统元件及调节控制器的动态特性，基于线性化代数方程，用代数判据进行系统的小干扰稳定性分析，如采用功角稳定分析中常用的dP/dδ判据等，这种小干扰稳定分析称为静态稳定分析。因此可以认为：动态稳定分析是严格的小干扰稳定分析，静态稳定分析是简化的小干扰稳定分析，而暂态稳定分析指的是大扰动时电力系统的稳定性分析。

发电机电动势E向容量无限大的系统母线电压V输电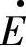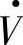，、之间的相角差为δ，电抗为X。在图1-7中，当工作点在δ<90°区域，如在A点P_e=P₀，δ=δ₀，电力系统稳定工作。如果系统受到小扰动以至δ从δ₀→δ₁（C点）时，由于原动机功率P₀来不及改变，电磁功率P_e=EVsinδ₁/X>P₀，因而发电机的电磁阻转矩T_e>T₀（原动机转动力矩），转子加速度为负值，致使转子减速，相对速度Δω=dδ/dt<0又导致δ从δ₁→δ₀，即工作点从C点返回到A点。反之，当系统受到小扰动而使δ从δ₀减少到δ₂（D点）时，在δ<90°区域内，P_e=EVsinδ₂/X<P₀，因而发电机的电磁阻转矩T_e<T₀（原动机转动力矩），致使转子加速，Δω=dδ/dt>0，转子加速又导致δ从δ₂→δ₀，即工作点从D点返回到A点。因此，在δ<90°工作区域内发电机在遭受小干扰后，由于dP_e/dδ>0，在δ↑时P_e↑，使δ↓。在δ↓时P_e↓，使δ↑，故经过一个过渡过程后系统能够恢复到初始稳态运行，发电机或输电系统具有静态稳定性。

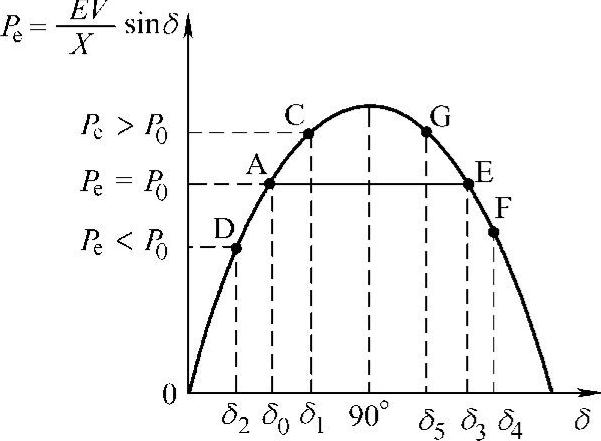
图1-7 小干扰稳定性分析图

在δ>90°区域，如图1-7中的E点，如果无任何小扰动，则δ=δ₃时P_e=P₀，系统同步稳定运行。但是一旦遭受微小的扰动后，δ从δ₃增加一点点到达δ₄（F点）时，P_e减小到P₄，由于dP_e/dδ<0，致使P_e=P₄<P₀，电磁阻转矩T_e<T₀（原动机转动力矩）导致发电机加速，δ从δ₄进一步增大。δ>δ₄后由于dP_e/dδ<0，使P_e变得更小，δ变得更大，因此电力系统发电机不再可能恢复到最初的E点同步稳定运行。类似的分析，当δ从δ₃受到小扰动后减小到δ₅（G点）时，由于dP_e/dδ<0，δ↓，P_e↑使T_e更大，发电机减速，δ会进一步减小，也不能回复到E点稳定工作，所以在δ>90°区域，系统不能稳定工作，即电力系统发电机在δ>90°区不具有小干扰时的静态稳定性，具有静态稳定性的运行区是δ<90°。

如图1-7所示，若正常运行在输出功率为P₀，而传输功率极限值为P_m=EV/X，则定义该运行工况下的静稳定储备系数K_P为

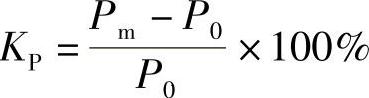
我国电力系统规定：在正常工况下K_P不应低于15%，在事故后的非常状态下K_P不应小于5%。

下面来分析图1-8所示电力系统遭受大扰动后的暂态稳定性。

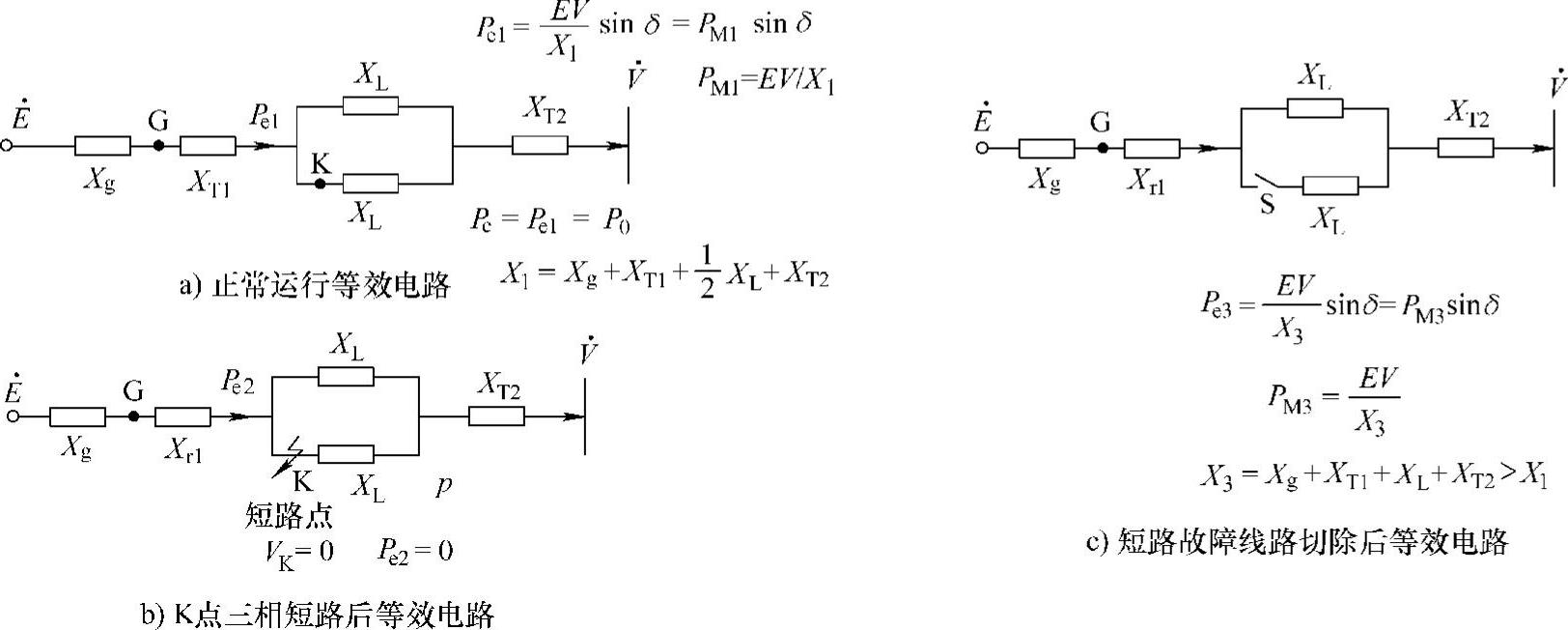
图1-8 电力系统暂态稳定分析电路

1）扰动前，假定发电机经双回路输电线向末端传输功率P_e1，原动机功率为P₀=P_e1。功率特性如图1-9中曲线①，输电功率的最大值P_M1=EV/X₁，工作点A，δ=δ₀。

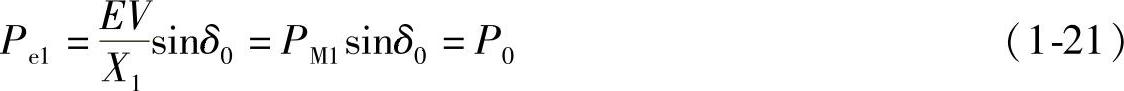
发电机的功角δ=δ₀恒定，相对运动速度Δω=dδ/dt=ω-ω_N=0，ω=ω_N。发电机角速度ω=ω_N（末端系统发电机同步角速度）。系统电抗为

X₁=X_g+X_T1+X_L/2+X_T2 （1-22）

2）如果图1-8中一条输电线首端K点发生三相短路故障，K点电压V_K=0，这时发电机输出的电磁功率P_e2=EV_Ksinδ/X₂=0，这时的电抗X₂=X_g+X_T1，电磁转矩T_e2=0。如果原动机P₀、T₀仍不变，短路后发电机输出的电磁功率点从图1-9a的A点转到D点，在不平衡转矩差ΔT=T₀-T_e2=T₀作用下，发电机转子加速运动，相对速度Δω=dδ/dt从零开始逐渐增大，δ逐渐加大，转子加速度d²δ/dt²与转子所受到的不平衡转矩差ΔT成正比，旋转物体的功率P等于转矩T与机械角速度Ω的乘积，即T=P/Ω，T与P成正比，ΔT与ΔP成正比，ΔT=ΔP/Ω。若ω=ω_N+Δω，ω_N为额定角频率，则dω/dt=dΔω/dt=d²δ/dt²，忽略摩擦阻力功率P_d，由转子运动方程式（1-20C）得

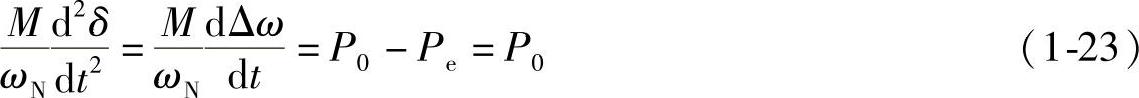
式中，P₀、P_e均为标幺值；M、t的单位为s。

短路期间V_K=0，P_e2=0。工作点从图1-9的A点转到D点，然后从D点向E点增大δ，如果经历时间Δt，相对速度Δω达到Δω_C，δ达到δ_C时，短路线路被开关切除，则由式（1-23）可得：

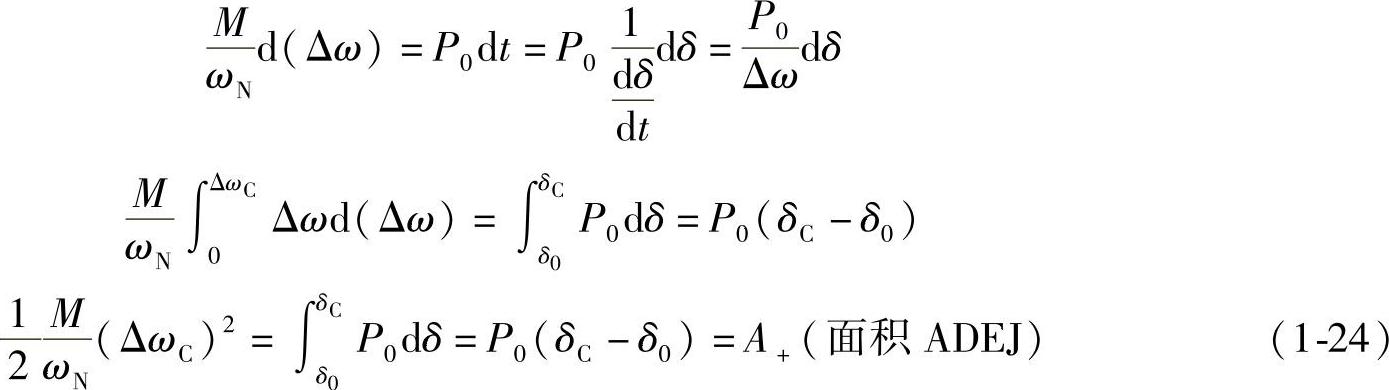
在短路存在的Δt期间，发电机输出的电磁功率P_e2=0，功率轨迹是图1-9a中的DE线。如果K点不是三相短路，例如两相短路，则在短路期间的正序等效电路中，K点对地应接入一个正序的电抗X，短路点K的正序电压V_K≠0，发电机电磁功率P_e2≠0，因此两相短路时发电机不平衡情况要好于三相短路。如果这时电力系统有并联补偿器能提高节点电压增大发电机电磁功率，则能进一步改善暂态稳定性。(www.xing528.com)

3）δ=δ_C时，Δω=Δω_C，切除短路线路后，发电机电磁功率为

P_e3=EVsinδ/X₃=P_M3 sinδ （1-25）

式中 X₃=X_g+X_T1+X_L+X_T2>X₁

这时的最大功率为P_M3=EV/X₃<P_M1=EV/X₁ （1-26）

因此，短路切除后发电机的电磁功率将是图1-9中的曲线③，运行点从图1-9的E点转到C点。这时P_e3（δ_c）>P₀。因此发电机转子所受到的转矩差ΔT=T₀-T_e3<0，转子相对运动的加速度为负值，相对运动速度Δω开始减小：

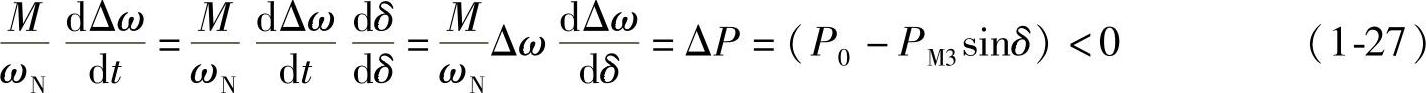
因此从δ=δ_C、Δω=Δω_C开始，转子相对运动速度Δω逐渐减小（加速度为负值），但δ仍继续增大（相对速度Δω仍为正值），工作点沿图1-9a中的特性曲线③从C点向上运动。如果到达δ=δ_F时，Δω→0，则在δ=δ_C到δ=δ_F期间，Δω从Δω_C减小到零。因此由（1-27）式得到

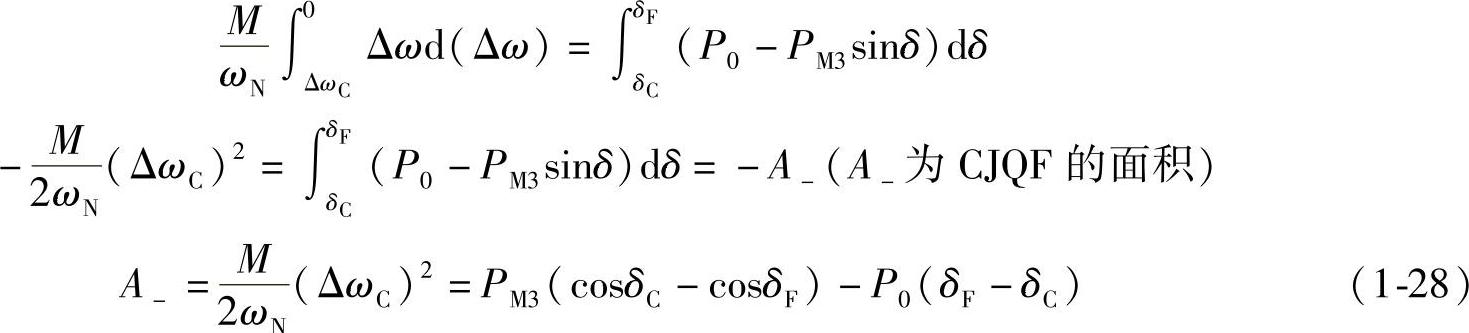
图1-9a中画出了短路前正常运行时的电磁功率曲线P_e1和短路切除后的电磁功率曲线P_e3，在短路期间发电机加速运行，δ从δ₀→δ_C，到达δ_C时的相对速度达到Δω=Δω_C。由式（1-24）可知，Δω_C可由短路期间图1-9a中的加速面积A₊确定。短路切除后，在δ从δ_C→δ_F期间，发电机减速运行，相对运动速度Δω从Δω_C减小到零。由式（1-28）和图1-9a可知，从Δω=Δω_C→Δω=0，δ从δ_C→δ_F期间的减速面积A-应与式（1-24）加速面积A+大小相等，即图1-9a中面积CJQF等于面积ADEJ。又由图1-9a和式（1-24）、式（1-28）可知：短路期间加速面积越大，相对速度Δω_C也越大，在短路切除后的减速期间，当减速到减速面积A-等于加速面积A+时，相对速度才回到零。如果这时运行工作点F的P_e3（δ_F）>P₀，则发电机转子所受的电磁阻转矩T_e3大于原动机转动力矩T₀，发电机转子会转为减速运动，Δω变负，δ从F点的δ_F开始减少，电磁功率P_e3从图1-9a中的F点沿曲线③移动经C点，再到B点。到达B点后，虽然P_e3=P₀，但这时Δω为负值，故δ将从B点的δ_B继续减小，δ<δ_B后，P_e3<P₀，转子又开始正加速度运行，到达δ=δ_G，工作点为曲线P_e3上的G点，Δω从最大负值减小到零，然后在加速转矩的作用下Δω为正值，又使δ增大到δ_B，然后在B点附近来回摆动几次，最终稳定在新的工作点B，恢复到同步稳定运行，P_e3（δ_B）=EV sinδ_B/X₃=P₀。图1-9a还画出了相对运动速度Δω。在图1-9a所示的情况下，即初始稳态运行在δ=δ₀、P_e1=P₀，遭到短路大扰动后，经历短路时间Δt，在δ=δ_C时切除故障线路后，又经过一个过渡过程仍然达到一个新的稳定的工作点δ=δ_B、P_e3（δ_B）=P₀同步稳定运行，我们称之为具有暂态稳定性。

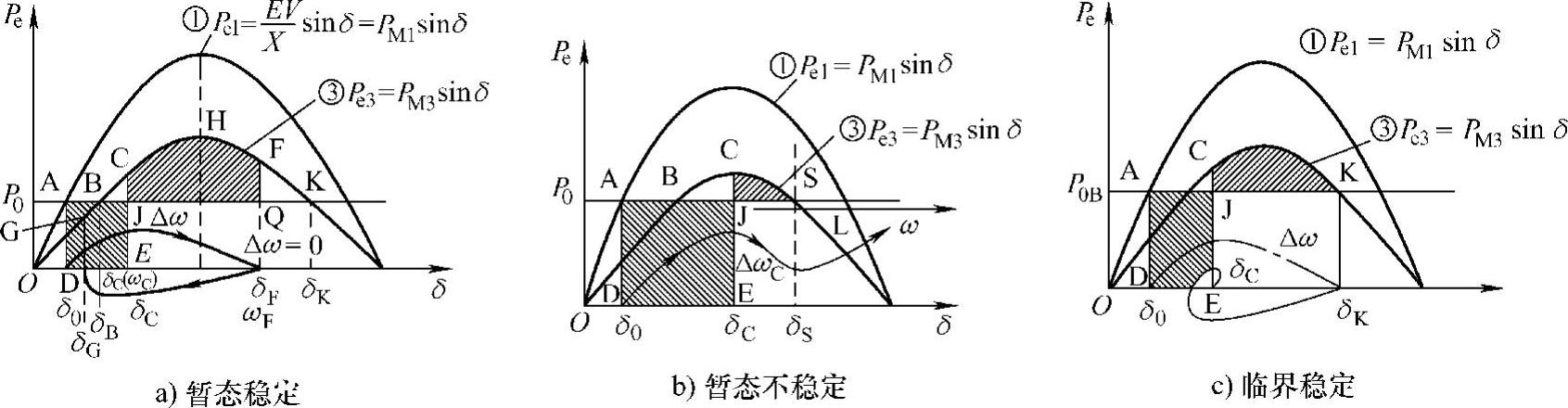
图1-9 暂态稳定特性

如果短路故障前发电机经输电线路传输的功率很大，P₀=P_e1=EVsinδ₀/X=P_M1 sinδ₀较大，而输电距离又较长，系统的电抗X₁较大，电磁功率最大值P_M1不是很大，则正常工作时功角δ₀就较大。此外，如果短路后，故障线路不能很快切除，即在短路期间的加速面积A+（面积ADEJ）较大，如图1-9b所示。切除故障时δ_C已经很大，相对运动速度Δω_C很大，这时故障切除后的减速期间运行点从C点移至S点时减速面积仍小于加速面积。到S点时相对运动速度Δω仍未下降到零，于是δ继续增大，而一旦δ>δ_S，例如在图1-9b中到达L点，P_e3<P₀，发电机又开始加速，δ进一步增大，δ加大使P_e3更小，使Δω更大，δ更大，因此δ一直不停地加大，发电机再也不能恢复到Δω=0的同步稳定运行，这种情况下，电力系统就不具有暂态稳定性。

如果在切除故障后的减速过程中运行点移到K点时正好减速面积等于加速面积（见图1-9c），那么在K点Δω=0，P_e3=P₀。由式（1-24）、式（1-28）两式令A+=A-可以得到这种临界情况时的运行参数的关系。这时的P₀是临界（极限，critical）暂态稳定时的最大输电功率P0crit。由A+=P0crit（δC-δ0）=A-=PM3（cosδC-cosδK）-P0crit（δK-δC）得到

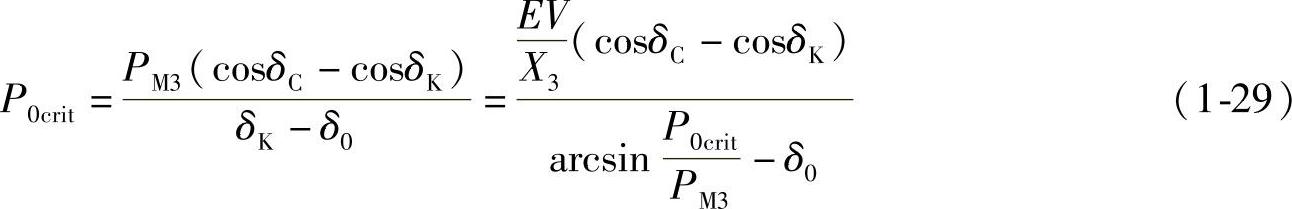
当稳态运行时的输电功率P>P_0crit时，暂态不稳定；当P<P_0crit时，暂态稳定。为了增大临界（极限）暂态稳定时的最大输电功率，提高或改善暂态稳定性，由式（1-29）可知，可以采用以下措施：

1）提高P_M3，增大减速面积。快速调控发电机励磁电流增大电动势E，通过无功补偿提升短路切除后的电压V，均可增大P_M3。

2）快速切除故障，减少加速面积，这时δ_C小，cosδ_C大，P_0crit增大。

3）减小输电线的等效电抗，电抗越小，使P_M3大、P_M1大、δ₀小，使P_0crit加大。

4）在短路期间，在图1-8b所示的发电机端点G处并接一个电阻增加短路时发电机的输出功率，减小短路期间发电机转子的加速转矩，减小加速面积，也可增大临界稳定功率P_0crit，改善电力系统发电机的暂态稳定性。

以上四个技术措施都可以通过在电力系统中采用电力电子技术和引入电力电子补偿控制器实现。

此外，如果在每条输电线首端（母线）装设电力电子开关限流型固态限流断路器，则短路时短路支路等效电抗将从零增大为限流电抗X_k，这将使短路时发电机输出功率不为零，减少加速功率，提高发电机的暂态稳定能力。