发电机功角特性优化方案

电力系统正常运行的一个重要标志是系统中所有的交流同步发电机都处于同步运行。所有并联在电网上运行的交流发电机都有绝对相同的电气角速度，发电机输出电压的频率都绝对相等。图1-6a所示的有两个发电机G₁、G₂的双回路输电线路的交流电力系统中，若两个发电机由转子励磁电流所产生的空载电动势分别为E₁、E₂，定子绕组电抗为X_g1、X_g2，则正常运行时首端发电机（电动势E₁）输送到末端E₂处的有功功率为

P=E₁E₂ sinδ/X

式中，系统的电抗X=X_g1+X_T1+X_L/2+X_T2+X_g2；δ是首端发电机电动势E·₁超前末端电动势E·₂的相位角。当发电机的电动势E₁和E₂均为恒值时，传输功率P是δ的正弦函数（见图1-6b），由于传输功率的大小与相位角δ密切相关，因此又称δ角为“功角”或“功率角”。传输功率与功角的关系P=f（δ），称为“功角特性”或“功率特性”。

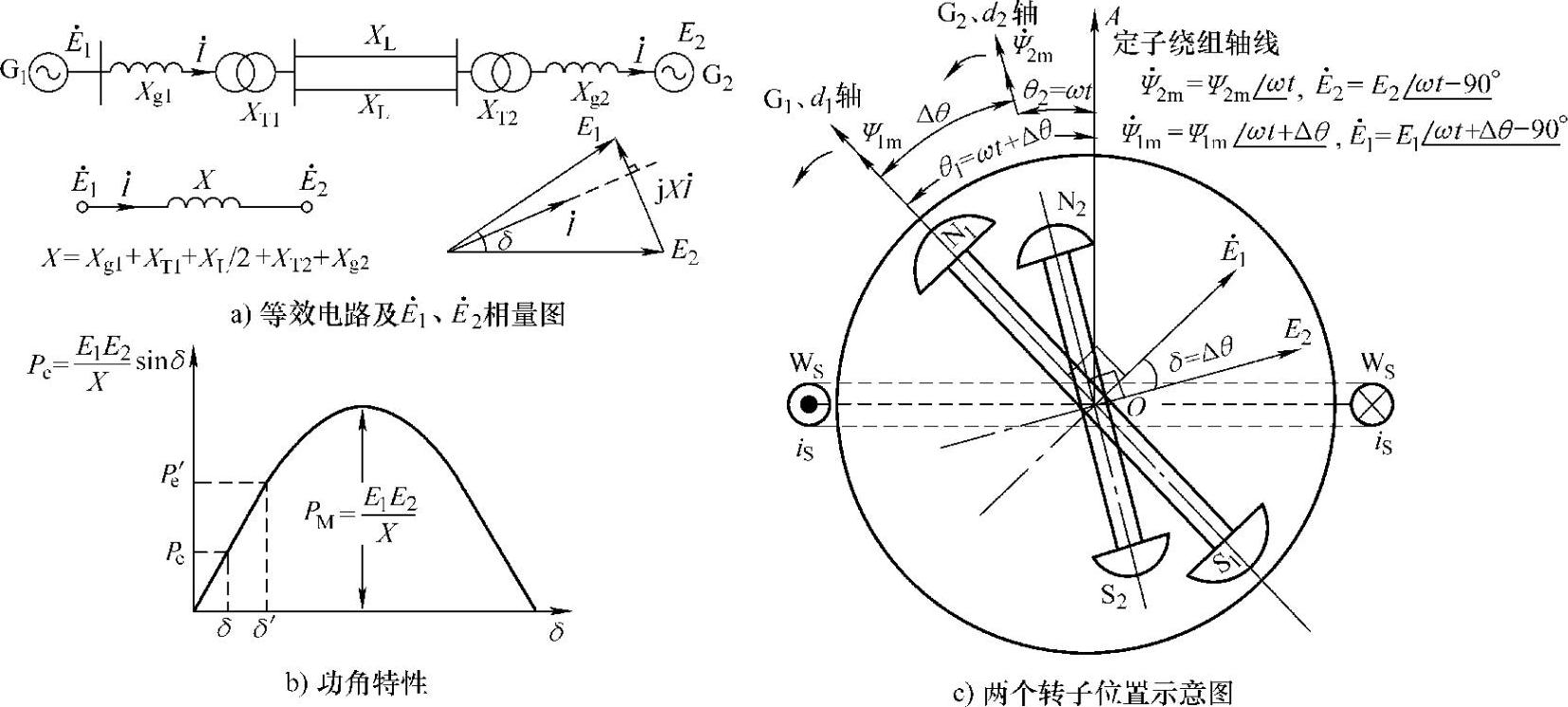
图1-6 双电源系统运行功角特性示意图

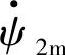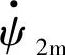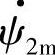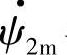在图1-6c中，取发电机G₁、G₂定子绕组W_S的空间位置在水平方向上，OA为定子绕组W_S的轴线，若发电机磁极对数N_p=1（两极电机），则转子机械角速度Ω与电气角速度ω=2π f相同。若G₁、G₂转子磁极的直轴d₁、d₂以角速度Ω=ω/N_p=2πf逆时针旋转，t=0时，G₂的磁极直轴d₂初始位置在方向，则任意瞬间t时，G₂转子空间位置θ₂=ωt；若G₁的转子直轴d₁位置超前G₂一个角度Δθ，则任意瞬间t时，G₁转子直轴d₁的位置角为θ₁=ωt+Δθ，若G₂的直流励磁电流产生的d₂方向的磁链为，由图1-6c可知，与OA的夹角为ωt，在方向的分量ψ_2m cosωt就是与定子绕组交链的磁链ψ_2s（ψ_2s=ψ_2m cosωt），G₂定子感应电动势瞬时值E₂（t）=-dψ_2s/dt=ωψ_2m sin ωt=E_2m cos（ωt-90°），即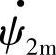产生的电动势E·₂的幅值E_2m=ωψ_2m，E₂的时间相位（ωt-90°）比磁链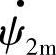的相位（ωt）滞后90°，同理G₁转子励磁电流产生其直轴d₁方向上的磁链为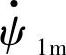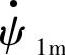，与G₁定子绕组交链的磁链ψ_1s=ψ_1mcos（ωt+Δθ），在G₁定子中产生的电动势E₁（t）=-dψ_1s/dt=ωψ_1m sin（ωt+Δθ）=E_1mcos（ωt+Δθ-90°），电动势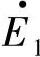的幅值E_1m=ωψ_2m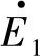，的时间相位（ωt+Δθ-90°）比磁链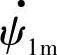的相位ωt+Δθ滞后90°。同时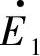，的相位（ωt+Δθ-90°）赶前E·₂的相位（ωt-90°）为Δθ，由图1-6a的电动势相量图可知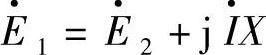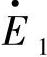，，超前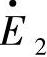的相角是δ，因此两个发电机转子空间位置相差角Δθ就是两个电动势相量的时间相位角δ：Δθ=θ₁-θ₂=δ。从另一个角度分析，在图1-6c中，E·₂滞后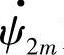为90°，E·₁滞后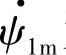为90°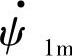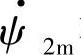，、在空间位置上的相差角Δθ（也是两个转子在空间位置上的相差角）当然就等于电动势相量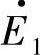、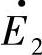之间的相差角δ。以上分析是磁极对数N_p=1的情况，在N_p≠1时类似。只是在N_p≠1时两个转子磁链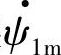、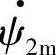在空间位置上的相差角Δθ=θ₁-θ₂=δ/N_p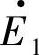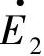，、的相位差δ=N_p Δθ，δ与Δθ有一个固定的比例关系。在G₁、G₂同步运行时，δ为恒值；当G₁、G₂不同步运行时，δ（t）=N_p Δθ（t）完全能反映两个转子的相对运动特性。如果G₂是一个容量远大于G₁的等效发电机，以致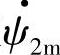随其转子一起恒速旋转，则δ（t）就可代表首端发电机G₁转子的相对运动特性，其相对运动电气角速度Δω=dδ/dt，相对加速度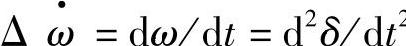，因此，功率角δ在电力系统稳定问题的研究中占有特别重要的地位。δ不仅表示电动势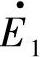超前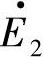的时间相位差，还表明了首端发电机G₁的转子与末端等效发电机G₂转子之间的相对空间位置（故又称为发电机转子“位置角”）。δ随时间的变化描述了两个发电机转子间的相对运动，而发电机转子间的相对运动的性质，恰好是判断各发电机之间是否同步运行的依据。

正常运行时，发电机输出的电磁功率P_e等于原动机的驱动功率P₀。此时，发电机转子上作用着两个转矩（不计摩擦等因素）：一个是原动机的驱动转矩T₀（或用功率P₀表示，功率P₀等于转矩T₀与机械角速度Ω₀的乘积，P₀=T₀Ω₀），它推动转子旋转；另一个是与发电机输出的电磁功率P_e对应的电磁阻转矩T_e（P_e=T_eΩ₀），它阻止转子旋转。在正常的情况下，两者相互平衡，即T₀=T_e（P₀=P_e），转子加速转矩ΔT=T₀-T_e=0，加速功率ΔP=P₀^-P_e=0，因而发电机以恒定速度ω旋转，且与末端系统的发电机的转速（指电角速度）相同（设为同步速度ω_N），ω=ω_N，即两者同步运行，功角δ=δ₀（见图1-6a和图1-6b）保持不变。在P_e=P₀、T_e=T₀、ω=ω_N、δ=δ₀恒定不变的稳态工况时，图1-6b中如果增大首端发电机的原动机功率到P₀′（即P₀′>P₀），原动机转动力矩T₀′>T_e，则在δ角尚未改变的情况下有P₀′>P₀=P_e=E₁E₂ sinδ₀/X，发电机功率不平衡，T₀′=P₀′/Ω₀>T_e=P_e/Ω₀，发电机受到的驱动转矩大于电磁阻转矩，迫使发电机转子加速运动，首端发电机转子相对于末端电网等效发电机转子加速运动，使两个转子的空间位置角（即功角）或电动势E₁超前电动势E₂的相位角δ增大，发电机的转速ω超过电网等效发电机的恒定转速ω_N，ω-ω_N=dδ/dt>0。随着δ的加大，发电机输出的电磁功率P_e=E₁E₂ sinδ/X也加大，首端发电机转子所受到的电磁阻转矩T′_e也随之加大，直到T′_e=T₀′，P_e′=P₀′为止。此时作用在首端发电机转子上的转矩再次达到新的平衡，功率也达到新的平衡，δ=δ′₀恒定不变，首端发电机转速又恢复与末端相同，Δω=ω-ω_N=dδ/dt=0、ω=ω_N，系统在新的工况δ=δ₀′，P_e′=P₀′=E₁E₂ sinδ₀′/X下恢复到同步稳定地运行。

如果只考虑原动机施予发电机转子的机械动力矩T₀（T₀对应的机械功率P₀=ΩT₀，Ω为机械角速度）和发电机产生并输出给电网的电磁功率P_e所对应的电磁阻转矩T_e（P_e=ΩT_e），则在不平衡转矩ΔT=T_e-T₀或不平衡功率ΔP=P_e-P₀作用下，发电机转子加速运动。加速度dω/dt≠0时，转子的运动方程为

式中，Ω是转子机械角速度；电气角速度ω=N_pΩ；发电机磁极对数N_p=ω/Ω=ω_N/Ω_N。ω_N、Ω_N是电机额定电气角速度和额定机械角速度，单位为rad/s（弧度/秒）；J是转子转动惯量。采用相对单位制（标幺制），如果取转矩T的额定值T_N为转矩基准值，则转矩标幺值（相对值）T_∗=T/T_N。取额定电气角速度ω_N（ω_N=2πf）为电气角速度基值，则电气角速度标幺值ω∗=ω/ω_N，Ω_N为机械角速度基准值，Ω_N=ω_N/N_P；取额定功率S_N=T_NΩ_N为功率基准值，则功率标幺值P_∗为

P_∗=P/S_N=P/T_NΩ_N=TΩ/T_NΩ_N=T∗Ω/Ω_N=T_∗ω/ω_N=T_∗ω_∗

转矩标幺值为

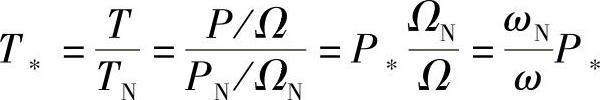
若ω=ω_N，则T_∗=P_∗，在发电机转矩、功率不平衡的实际暂态过程中，功角δ=δ₀+ωt变化虽大，但在短暂的暂态过程中或在转子摇摆过程中ω与ω_N仍十分接近，可以认为ω≈ω_N，因此，转矩标幺值T∗近似等于功率标幺值P∗，不平衡量ΔT∗=ΔP_∗。

在式（1-20A）左右两边都除以转矩基准值T_N=S_N/Ω_N，则可变为

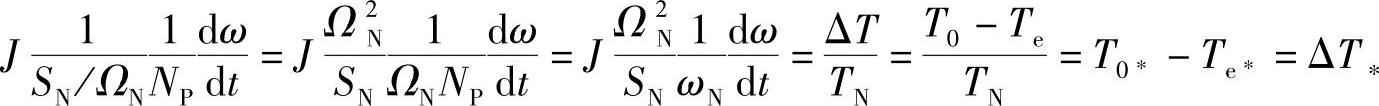(www.xing528.com)

由上式得到

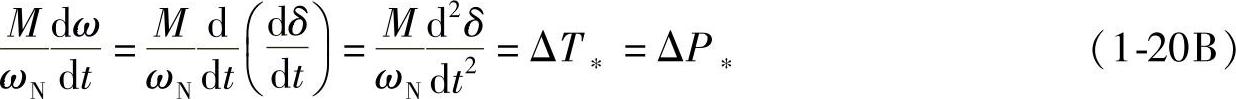
式中，M为转子的惯性时间常数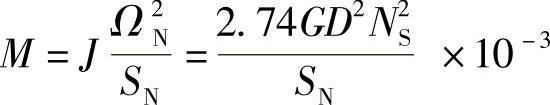，，单位为s；G为发电机转子的质量；D为转子直径，GD²单位为N·m²；N_S为发电机额定转速（即同步转速单位为r/min）。

式（1-20B）中ΔT_∗=T_0∗-T_e∗=ΔP_∗=P_0∗-P_e∗，由此得到

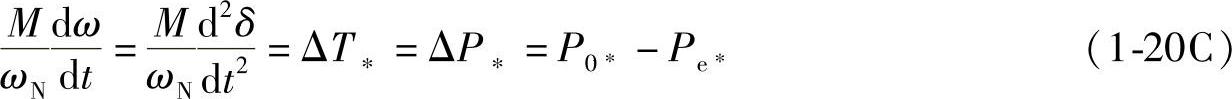
或

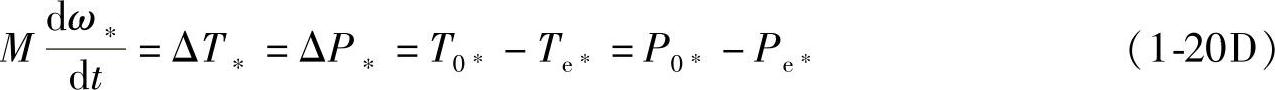
式中，M、t的单位为s；ω_∗、ΔT_∗、ΔP_∗、T_0∗、T_e∗、P_0∗、P_e∗都是标幺值。如果时间t也用标幺值，取时间基值为1/ω_N，则时间t的标幺值t∗=ω_Nt。若式（1-20D）中以s为单位的惯性时间常数M也用标幺值M∗表示，则式（1-20D）变为

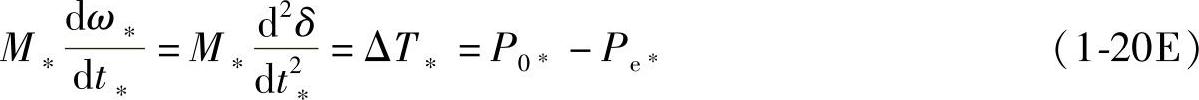
如果考虑转子以ω旋转时的摩擦阻力矩为T_d，T_d与ω成正比，T_d=Dω，标幺值T_d∗=T_d/T_N=Dω/T_N=D₀ω，D₀=D/T_N为摩擦阻力矩系数，则转子运动方程中应该增加一项摩擦阻力矩T_d∗，由式（1-20C）得到

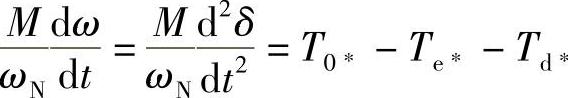
这时转子运动方程为

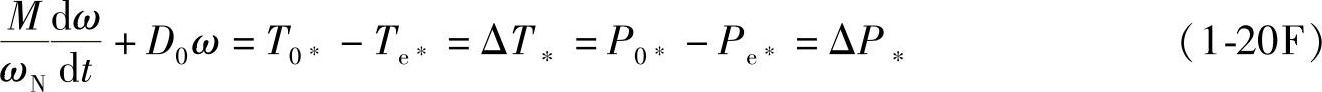
转子运动方程可用于研究暂态中发电机的动态特性和电力系统的动态工况。请读者留意：部分书刊、文献中，为了书写简洁，常将运动方程中的标幺值符号∗省去。