图1-2a所示为最简单的输电系统中，首端（或送端）发电机Gs通过升压变压器T-1、双回路输电线L、降压变压器T-2接到输电线末端（或受端）电力系统等效发电机Gr。如果末端等效发电机Gr容量相对于首端发电机而言很大，则首端发电机输送任何功率时，末端母线电压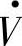
的幅值、相位、频率均不变，即末端等效为无限大容量的母线。若首端发电机为隐极同步发电机，忽略发电机、变压器和输电线的等效电阻R时，可以得到系统的等效电路图1-2b。图中E为首端发电机Gs的电动势、V为末端母线的电压，Xg、XT1、XT2和XL分别为发电机、升压变压器、降压变压器和单回路输电线电抗，则系统的总电抗X为
X=Xg+XT1+XT2+XL/2 （1-1）
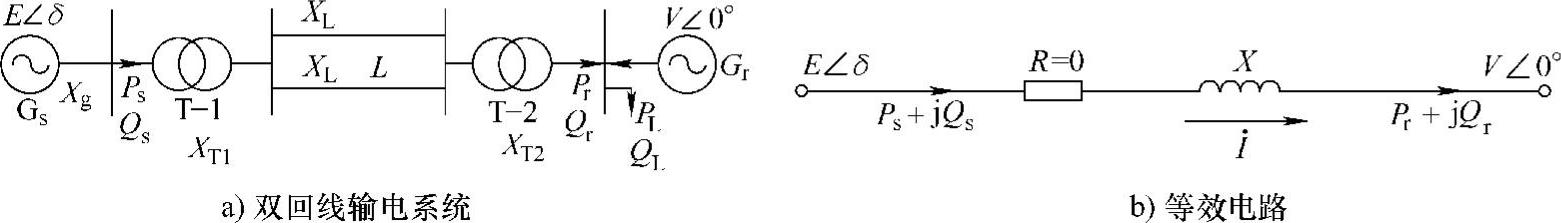
图1-2 简单电力系统及其等效电路（R=0）
发电机、变压器和输电线路的电阻远小于电抗，因此，若图1-2b中全系统的等效电阻R近似为零，采用相对值（标幺值）表示电力系统的参数，由等效电路图1-2b可以得到
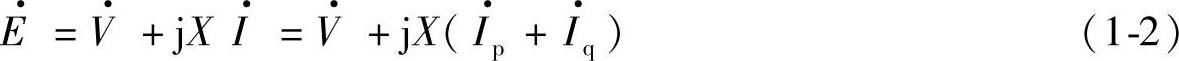
图1-3a和图1-3b给出电流I·超前电压V·和I·滞后V·两种工况下的电压、电流相量图。图中，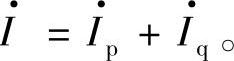
两种工况都是首端电动势E·的相位超前末端电压
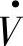，相位超前角δ又称为功率角。若电压V·相位为0°，
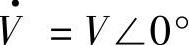，则电动势E·=E∠δ。图1-3a中电流I·超前电压
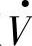的角度为φ2，
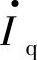对
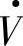而言为容性无功电流I·qC；图1-3b中电流I·滞后电压
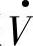的角度为φ2，
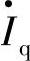对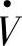
为感性无功电流I·qL。图1-3a和图1-3b中取
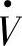在水平坐标轴d（p）方向，即
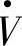的相位角为零。取超前d（p）轴90°的方向为q轴（容性q轴）。因此I·在d（p）方向的分量为有功电流Ip，I·在q轴方向的分量为无功电流I·q。对于图1-3a所示的工况，即I·的相位角为φ2，则有
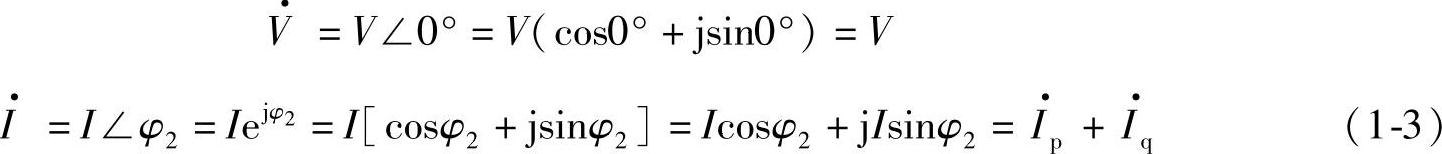
有功电流相量为
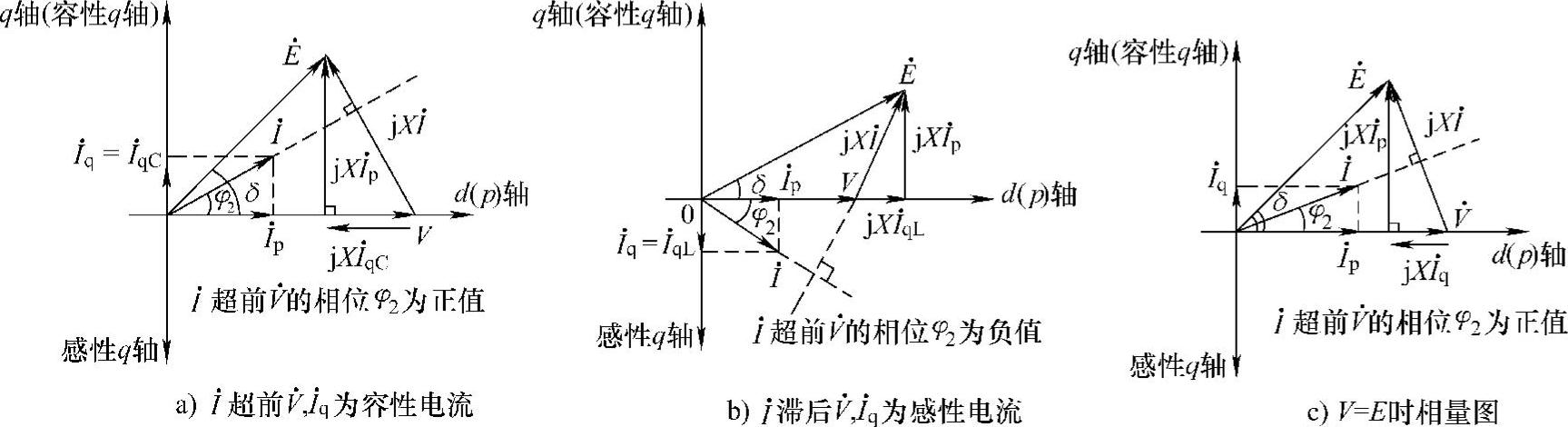
图1-3 简单电力系统相量图（R=0）
在图1-3a中I·q对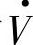
而言为容性（超前）无功电流相量，即
I·q=jIsinφ2=jIq=jIqC （1-5）
又有Ecosδ=V-XIqC，输出容性（超前）电流I·q为
又Esinδ=XIp，输出有功电流Ip为
首端电源（E·）经输电系统送至末端（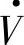
）的有功功率Pr为
式中，P、V、E为相对单位制中的标幺值。在相等单位制中，三相功率等于单相功率。
首端电源（E·）经输电系统送到末端V的容性（超前）无功功率为
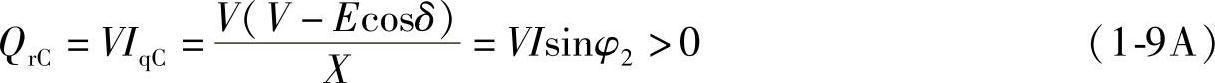
容性（超前）无功功率QrC等效于负值的感性（滞后）无功功率QrL，即QrC=-QrL，图1-3a中，I超前V，电压V大于E cosδ，首端电源（E）经输电系统送到末端电压V的感性（滞后）无功功率QrL为
对于图1-3b所示工况，Iq为滞后（感性）无功电流IqL，Ecosδ=V+XIqL。
输出感性（滞后）无功电流为
又Esinδ=XIp，则输出有功电流为
图1-3b中，I·滞后于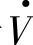
，首端电源（E·）经输电系统送到末端V处感性（滞后）的无功功率Qr为
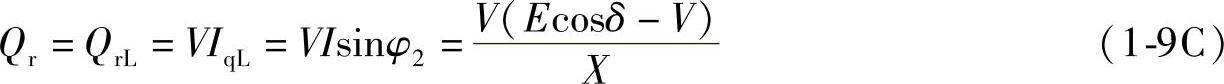
图1-3a和图1-3b中，E·超前于
，即δ>0时，由式（1-7A）、式（1-8）可知，Ip>0，Pr>0，首端电源E·经线路向末端送电；若E·滞后于
，即δ<0时，由式（1-7A）、式（1-8）可知，Ip<0，Pr<0，则末端电源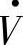
经线路向首端送有功功率。因此在两个电源E·、
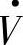之间，有功功率总是从相位超前的电源送至相位滞后的电源。
如果E的数值比V大得很多，以至于Ecosδ>V（见图1-3b），则首端电源E·经输电系统送至末端的感性（滞后）无功功率QrL为式（1-9B），QrL>0；若V较大，以致V的数值大于Ecosδ，（见图1-3a），则首端电源E·经输电系统送至末端V处的电流为容性无功电流，对应的容性（超前）无功功率QrC为式（1-9A），等效于这时末端电源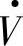
向线路输出感性滞后无功功率QrL=-QrC。因此感性（滞后）无功功率是从电压值高的电源输出到电压较低的电源。
在图1-3b中，首端发电机输出的有功功率Ps和感性（滞后）无功功率Qs为
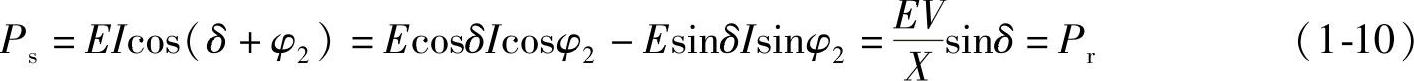
首端发电机输出的感性（滞后）无功功率为
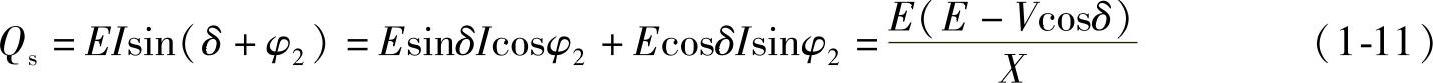
电力系统中电抗X所消耗的滞后无功功率QX为
由图1-3b可知（IX）2=E2+V2-2VEcosδ，故有
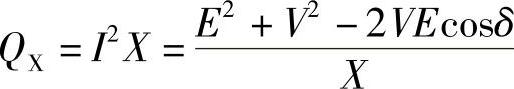
由式（1-9B）和式（1-11）有
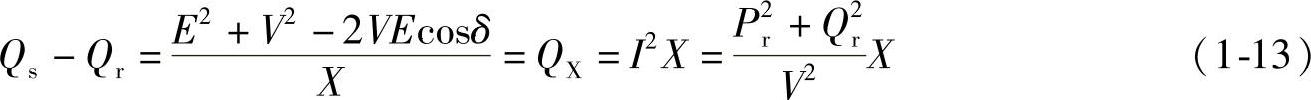
由式（1-10）可知，发电机输出的有功功率Ps等于送至末端的有功功率Pr（忽略了所有元件的电阻，故有功损耗I2R=0）。由式（1-13）可知，发电机Gs产生的感性（滞后）无功功率Qs经系统电抗X消耗I2X后，向系统末端输出的感性（滞后）无功功率为Qr=-VIsinφ2=Qs-QX=Qs-I2X。(www.xing528.com)
在实际电力系统中，如果像图1-3b中所示，流入末端的电流I·滞后
，φ2为负值，则末端负荷的感性滞后无功负荷也由首端电源E·经系统等效电抗X供给，则在输电系统中不仅引起较大的电压损耗，而且还有较大的有功功率损耗和无功功率损耗。
如果令电力系统中发电机、变压器、输电线路的全部无功损耗I2X由输电线路首、末两端电源（E·、
）平均负担，即令-Qr=Qs=I2X/2，则由式（1-9c）、式（1-11）或由图1-3可得到E=V，这时如图1-3c所示。I·滞后E·的角度为δ/2，I·超前
的角度也是δ/2，即I·超前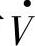
和I·滞后E·的角度都是δ/2，这时首、末两端的电源输出相等的感性（滞后）无功功率供输电系统中电抗的无功损耗。
在d、q坐标系中，取q轴超前d轴90°，复数功率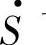
可以有两种表达式，即
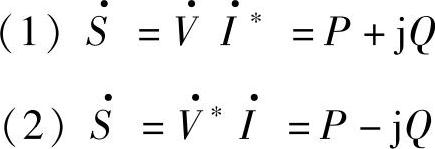
式中，I·∗为电流I·的共轭相量；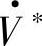
为
的共轭相量；Q为感性（滞后的）无功功率。若电流I·滞后电压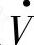
，则有功功率P为正，感性（滞后的）无功功率也为正值。由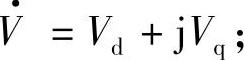
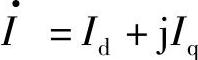，有
（1）若令：
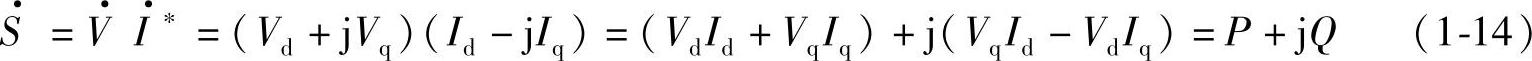
则有功功率为
P=VdId+VqIq（1-15A）感性（滞后）无功功率为
Q=VqId-VdIq（1-15B）
若取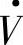
在d轴上，如图1-3所示，则Vd=V，Vq=0，这时取I=Id+jIq。Iq为正值时则为容性（超前）无功电流，Iq为负值时则为感性（滞后）无功电流。这时有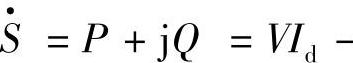
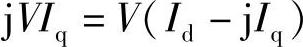，有功功率：P=VdId=VId：感性（滞后）无功功率：Q=-VdIq=-VIq。上式中，Id为与V同相的有功电流；Iq为超前V的容性无功电流；-Iq为感性（滞后）无功电流。
在图1-3b中，Id为正，P为正；Iq为负（感性、滞后电流），Q=-VIq为正（感性、滞后无功功率）。
在图1-3a中，Id为正，P为正；Iq为正（容性、超前电流），Q=-VIq为负（容性、超前无功功率）。
（2）若令：
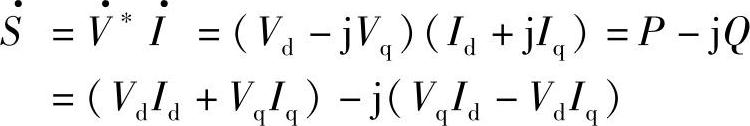
则有功功率为
P=VdId+VqIq
感性（滞后的）无功功率为
Q=VqId-VdIq
将以上P、Q表达式与式（1-15）对比可知，复功率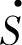
的两种表达式
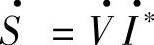=P+jQ和
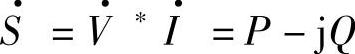中的P、Q是相同的。
图1-4a是一个更一般化带支路Z3的双电源输电系统网络，以下分析不忽略输电线路的电阻时输电系统的功率特性。图1-4b和图1-4c分别为末端电源V=0和首端电源E=0时的等效电路，I11、I21是V=0时的电流；I12、I22是E=0时的电流。由叠加原理有
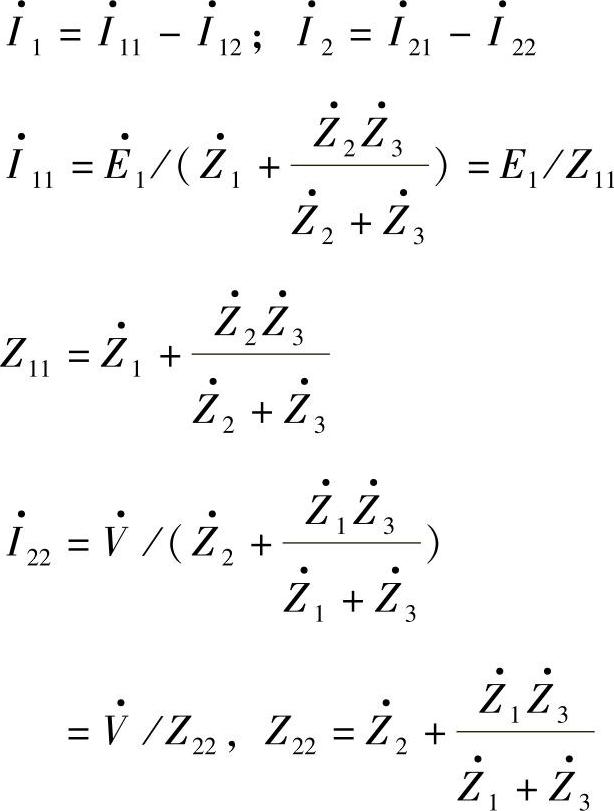
式中，Z11、Z22称为系统的输入阻抗。
又有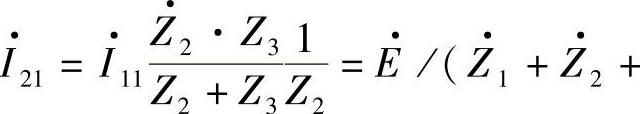
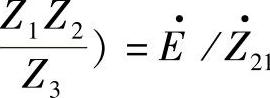
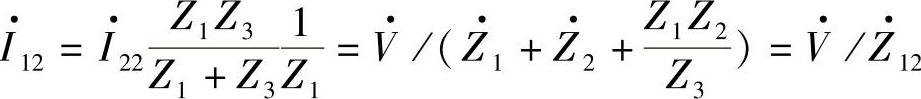
式中，Z·21=Z·12=Z1+Z·2+Z1Z2/Z3称为系统的转移阻抗。
因此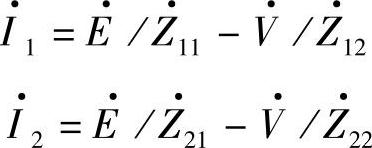
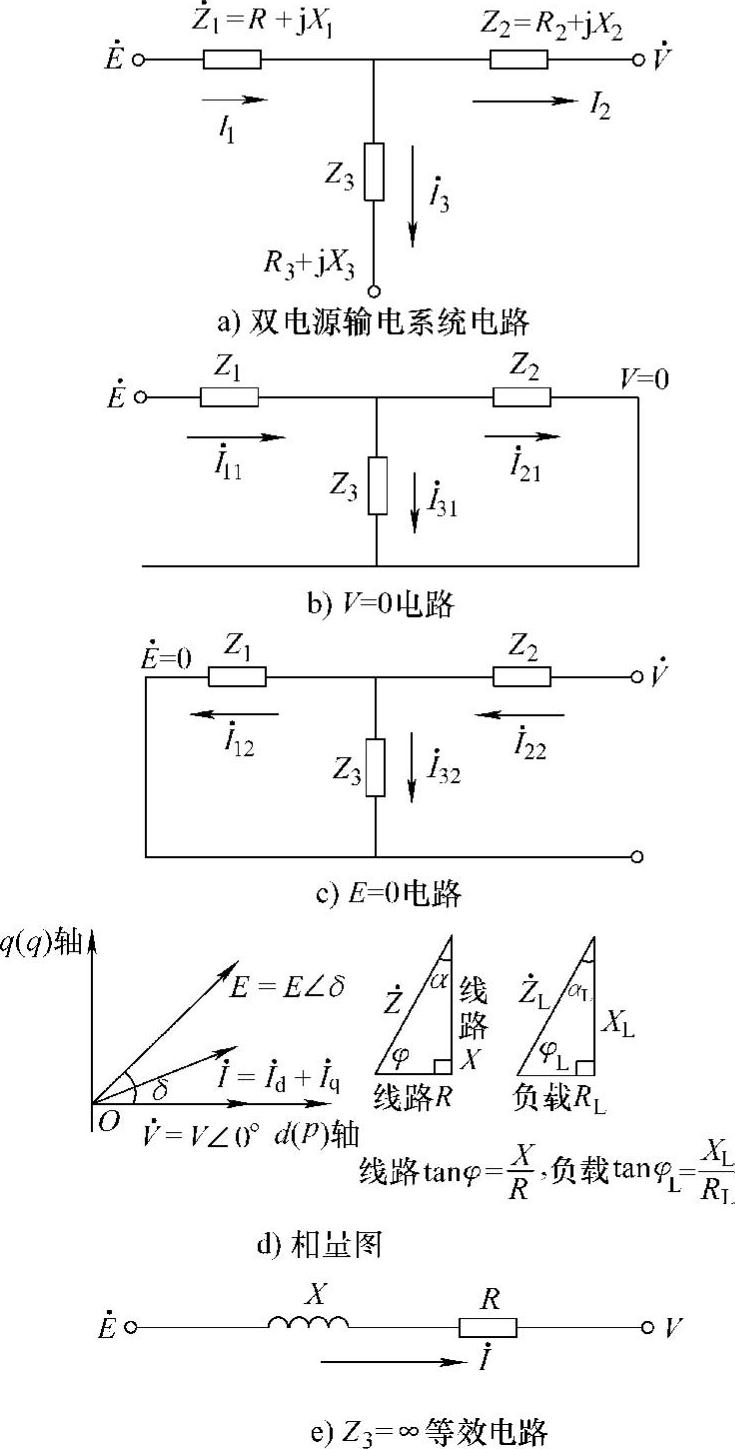
图1-4 带支路的双电源输电网络
若取
在水平轴方向上，
=V∠0°=V，E·超前
相角为δ，E·==E∠δ=E（cosδ+jsinδ）。
若输入阻抗和转移阻抗为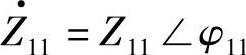
，
，
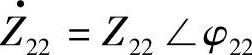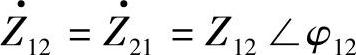，其中线路阻抗角分别为φ11=arctanX11/R11，φ22=arctanX22/R22，φ12=arctanX12/R12，X11、X22、X12、R11、R22、R12分别为阻抗Z11、
、
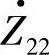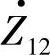的电抗和电阻，线路阻抗角的余角α=90°-φ，如图1-4d所示。线路首端功率为
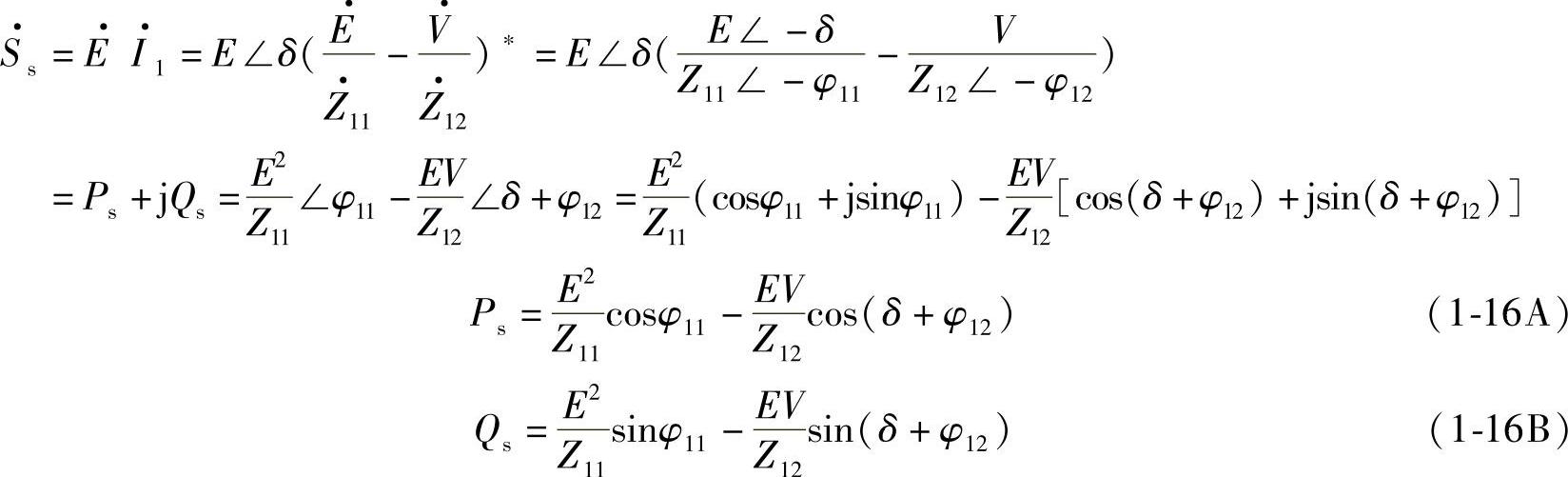
同理，由线路末端功率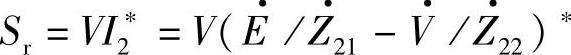
可得到
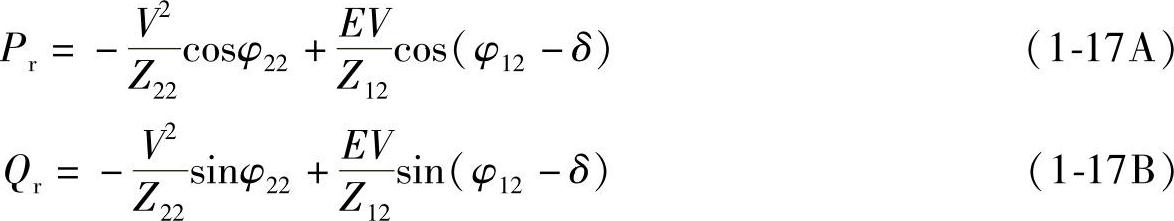
如果Z3支路不存在，即Z3=∞，则Z11=Z12=Z22=Z1+Z2=Z，，R11=R12=R22=R1+R2=R，X11=X12=X22=X1+X2=X，Z2=R2+X2，由于Z·=Z∠φ=Zcosφ+jZsinφ，R=Zcosφ，X=Zsinφ，tanφ=X/R，φ为线路阻抗Z1+Z2的阻抗角。式（1-16A）和式（1-16B）可简化为
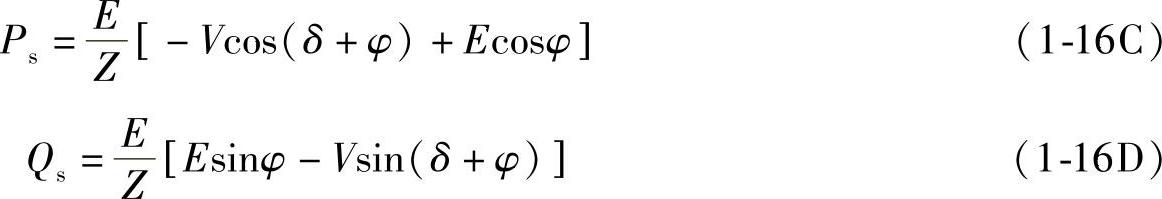
如果不考虑线路电阻，R=0，Z=X，阻抗角φ=90°，则式（1-16C）和式（1-16D）简化为式（1-10）和式（1-11）。
如果支路Z3不存在，即Z3=∞，式（1-17A）和式（1-17B）可简化为
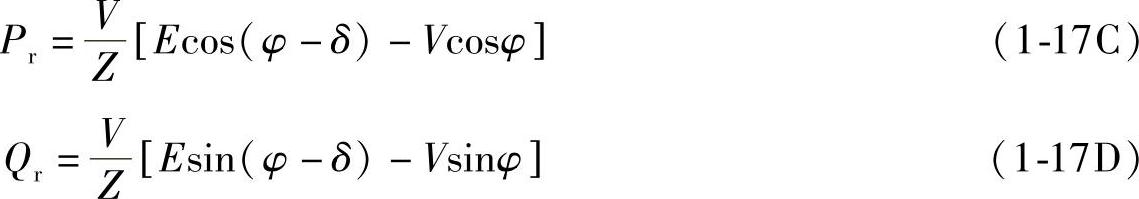
如果不考虑线路电阻，R=0，Z=X，阻抗角φ=90°，则式（1-17C）和式（1-17D）可简化为式（1-8）、式（1-9C）。有功功率为
感性（滞后）无功功率为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
