直线透视：深入理解

直线透视是物体透视的基础。

1.直线的迹点和灭点

（1）直线的迹点，即直线与画面的交点。如图5-13 所示，直线AB 的迹点为N1。

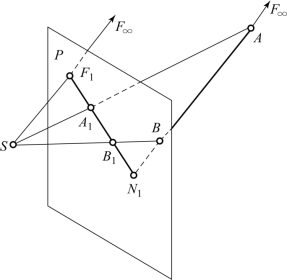
图5-13　直线的迹点和灭点

（2）直线的灭点，即直线上无限远点的透视。设直线AB 上无限远的点为（图5-13），如作此点的透视，只要过视点S 作视线平行于AB，该视线与画面的交点F1 即为直线AB 的灭点。

连接迹点与灭点的直线N1F1 称为直线的全透视，直线的透视位于直线的全透视上。

2.直线透视的主要特性

（1）画面内直线的透视为直线本身，反映直线的实长。

（2）与画面平行的直线，其透视与空间直线平行，但不反映直线的实长。如图5-14所示，由于AB∥P，则A1B1∥AB，但A1B1 ＜AB。(www.xing528.com)

推而广之，与画面平行的一组平行线，其透视相互平行。图5-15 中，直线Aa、Bb 和Cc 均为垂直于基面又平行于画面的直线，它们的透视彼此平行。

图5-14　画面平行线的透视（一）

图5-15　画面平行线的透视（二）

（3）点在直线上，点的透视必落在直线的透视上。当点处在与画面相交的直线上时，点的透视不再成定比分割直线的透视。如图5-13 所示，点B 在直线AN1 上，则AB∶BN1≠A1B1∶B1N1。只有当点处在与画面平行的直线上时，点的透视才成定比分割直线的透视。如图5-14 所示，由于AB∥P，所以AC∶CB=A1C1∶C1B1。

（4）与画面相交的平行直线，其透视相交于同一灭点。例如，图5-16 中两平行直线AN1 和BN2的透视A1N1 和B1N2 相交于同一灭点F1。

（5）一组长度相等的平行直线段，当画面位于它们之前时，距画面近的其透视陡度大，距画面远的其透视长度小，即所谓“近大远小”。如图5-15所示，Aa=Bb=Cc，而A1a1 ＞B1b1 ＞C1c1。又如图5-15 所示，AB=BC，而A1B1 ＞B1C1。这与人们日常观察物体时所见的效果相同，这也就是透视图真实感强的原因。

图5-16　与画面相交的平行线的透视