换面法：投影面的平行线、水平线和一般位置平面的变换方法

点是一切几何元素的基本元素。因此在研究换面法时，首先从点的投影变换开始来研究换面法的投影规律。

1.点的一次换面

1）换V 面

图2-32（a）表示点A 在原投影体系V/H 中，其投影为a 和a′。现令H 面不动，用新投影面V1 来代替V 面，V1 面必须垂直于不动的H 面，这样便形成新的投影体系V1/H，O1X1 是新投影轴。

过点A 向V1 面作垂线，得到V1 面上的新投影a′1，点a′1 是新投影，点a′是旧投影，点a 是新、旧投影体系中的共有的不变投影。a 和a′1 是新的投影体系中的两个投影，将V1 面绕O1X1 轴旋转到与H 面重合的位置时，就得到图2-32（b）所示的投影图。

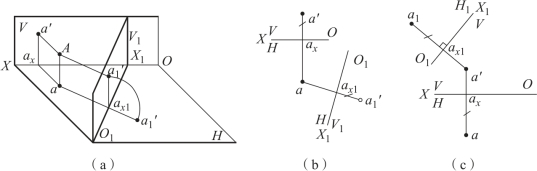
图2-32　点的一次变换（换V 面）

由于在新投影体系中，仍采用正投影方法，又在V/H 投影体系和V1/H 体系中，具有公共的H 面，所以点a 到H 面的距离（Z 坐标）在两个投影体系中是相等的。所以有如下关系：a′1⊥O1X1 轴；a′1ax1=a′ax=Aa。即换V 面时Z 坐标不变。

由此得出点的投影变换规律：

（1）点的新投影和不变投影的连线，必垂直于新投影轴；

（2）点的新投影到新投影轴（O1X1）的距离等于被替换的点的旧投影到旧投影轴（OX）的距离，即换V 面时高度坐标不变。

换V 面的作图方法和步骤如图2-32（c）所示：

（1）在被保留的H 投影a 附近（适当的位置）作O1X1 轴；

（2）由H 投影a 向新投影轴O1X1 作垂线，在此垂线上量取a′1ax1=a′ax，点a′1 即为所求。

2）换H 面

换H 面时，新旧投影之间的关系与换V 面类似，也存在如下关系：

a′a⊥O1X1 轴；a1ax1=aax=Aa′，换H 面时Y 坐标不变。

其作图方法和步骤与换V 面类似，可类推，此处省略。

2.点的二次换面

应用换面法解决实际问题时，有时一次换面还不便于解题，还需要二次或多次变换投影面。图2-33 表示点的二次换面，利用其求点的新投影的作图方法和原理与一次换面相同。

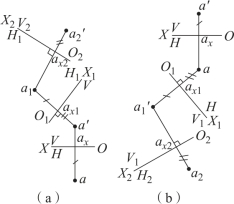
图2-33　点的二次换面

但要注意：在更换投影面时，不能一次更换两个投影面，为在换面过程中使两投影面保持垂直，必须在更换一个投影面之后，在新的投影体系中交替地再更换另一个。如图2-33（a）所示，先由H1 代替H 面，构成新的投影体系V/H1，O1X1 为新坐标轴；再以这个新投影体系为基础，以V2 面代替V 面，又构成新的投影体系V2/H1，O2X2 为新坐标轴。

二次换面的作图步骤如图2-33（b）所示：

（1）先换H 面，以H1 面替换H 面，建立V/H1 投影体系，得新投影a1，而a1ax1=aax=Aa′，作图方法与点的一次换面完全相同；

（2）再换V 面，以V2 面替换V 面，建立V2/H1 投影体系，得新投影a′2，而a′2ax2=a′ax1=Aa1，作图方法与点的一次换面类似。

根据实际需要也可以先换V 面，后换H 面，但两次或多次换面应该是V 面和H 面交替更换，如：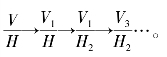

3.几个基本作图问题

1）将一般位置直线变换为投影面平行线

图2-34（a）所示为把一般位置直线AB 变换为投影面平行线的情况。用V1 面代替V面，使V1 面∥AB 并垂直于H 面。此时，AB 在新投影体系V1/H 中为正平线。图2-34（b）为投影图。作图时，先在适当位置画出与不变投影ab 平行的新投影轴O1X1（O1X1∥ab），然后根据点的投影变换规律和作图方法，求出A、B 两点在新投影面V1 上的新投影a′1、b′1，再连接直线a′1b′1。则a′1b′1 反映线段AB 的实长，即a′1b′1=AB，并且新投影a′1b′1 和新投影轴（O1X1 轴）的夹角即为直线AB 对H 面的倾角α，如图2-34（b）所示。

如图2-34（c）所示，若求线段AB 的实长和与V 面的倾角β，应将直线AB 变换成水平线（AB∥H1 面），也即应该换H 面，建立V/H1 新投影体系，基本原理和作图方法同前。

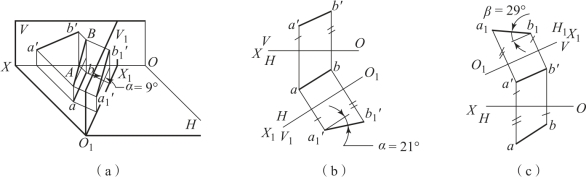
图2-34　将一般位置直线变换为投影面平行线

2）将投影面平行线变换为投影面垂直线

将投影面平行线变换为投影面垂直线，是为了使直线积聚成一个点，从而解决与直线有关的度量问题（如求两直线间的距离）和空间位置问题（如求线段面交点）。应该选择哪一个投影面进行变换，要根据所给直线的位置而定，即选择一个与已知平行线垂直的新投影面进行变换，使该直线在新投影体系中成为投影面垂直线。

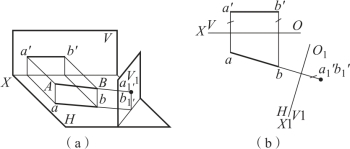
图2-35　将投影面的平行线变换为投影面垂直线

图2-35（a）表示将水平线AB 变换为新投影面的垂直线的情况。图2-35（b）表示投影图的作法：因所选的新投影面垂直于AB，而AB 为水平线，所以新投影面一定垂直于H 面，故应换V 面，用新投影体系V1/H 更换旧投影体系V/H，其中O1X1⊥ab。

3）将一般位置直线变换为投影面垂直线如果要将一般位置直线变换为投影面垂直线，必须变换两次投影面。先将一般位置直线变换为投影面平行线，然后再将该投影面平行线变换为投影面垂直线。

如图2-36 所示，先换V 面，使直线AB 在新投影体系V1/H 中成为正平线，然后再换H面，使直线AB 在新投影体系V1/H2 中成为铅垂线。作图方法详见图2-36（b），其中O1X1∥ab，O2X2⊥a′1b′1。

图2-36　直线的二次换面

4）将一般位置平面变换为投影面垂直面（求倾角问题）

将一般位置平面变换为投影面垂直面，只需使平面内任一直线垂直于新的投影面。我们知道要将一般位置直线变换为投影面垂直线，必须经过两次变换，而将投影面平行线变换为投影面垂直线只需要一次变换。因此，在平面内不取一般位置直线，而是取一条投影面平行线为辅助线，再取与辅助线垂直的平面为新投影面，则平面就和新投影面垂直了。

图2-37 表示将一般位置平面△ABC 变换为新投影体系中的正平线的情况。由于新投影面V1 既要垂直于△ABC 平面，又要垂直于原有投影面H 面，故它必须垂直于△ABC 平面内的水平线。

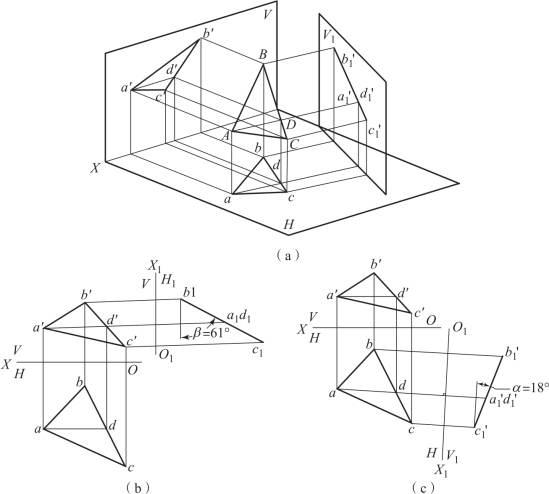
图2-37　平面的一次换面（求倾角）(www.xing528.com)

作图步骤，如图2-37（b）所示：

（1）在△ABC 平面内作一条水平线AD 线作为辅助线，同时作出其投影ad、a′d′；

（2）作O1X1⊥ad；

（3）求出△ABC 在新投影面V1 面上的投影a′1、b′1、c′1，a′1、b′1、c′1 三点的连线必积聚为一条直线，即为所求。该直线与新投影轴的夹角即△ABC 平面与H 面的倾角α。

同理，也可以将△ABC 平面变换为新投影体系V/H1 中的铅垂面，同时可求出△ABC 平面与V 面的倾角β。

5）将投影面的垂直面变换为投影面平行面（求实形问题）

图2-38 表示将铅垂面△ABC 变为投影面平行面（求实形）的情况。新投影面平行于△ABC，因此它必定垂直于投影面H，并与H 面组成V1/H 新投影体系。△ABC 在新投影体系中是正平面。图2-37（b）为它的投影图。

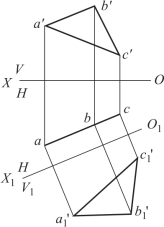
图2-38　将投影面的垂直面变换为投影面平行面

作图步骤，如图2-38 所示：

（1）在适当位置作O1X1∥abc；

（2）求出△ABC 在V1 面的投影a′1、b′1、c′1，连接此三点，△a′1b′1c′1 即为△ABC 的实形。

6）将一般位置平面变换为投影面平行面（二次换面）

要将一般位置平面变换为投影面平行面，必须经过两次换面。因为如果取新投影面平行于一般位置平面，则这个投影面也一定是一般位置平面，它和原体系V/H 中的哪个投影面都不垂直而无法构成新投影体系。因此，一般位置平面变换为投影面平行面，必须经过两次换面。

如图2-39（a）所示，先换V 面，其变换顺序为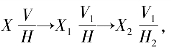 在H2 面上得到△a2b2c2≅△ABC，即△a2b2c2 是△ABC 的实形；

如图2-39（b）所示，先换H 面，其变换顺序为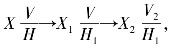 在V2 面上得到△a′2b′2c′2≅△ABC，即△a′2b′2c′c 是△ABC 的实形。

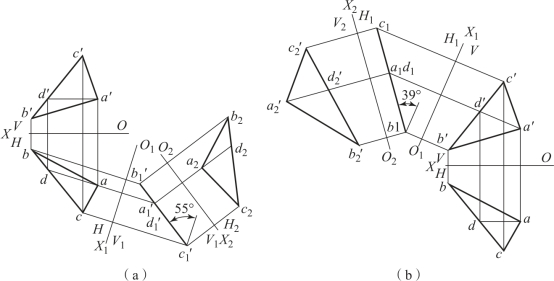
图2-39　平面的二次换面

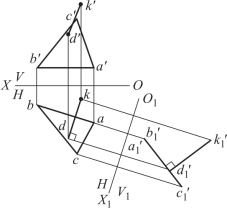
图2-40　点到平面的距离

4.应用举例

1）点到平面的距离

确定点到平面的距离，只要把已知的平面变换成投影面垂直面，点到平面的实际距离就可反映在投影图上了。

如图2-40 所示，用变换V 面的方法，确定点D 到△ABC 的距离，作图步骤如下：

（1）由于△ABC 中的AB 为水平线，故直接取新轴O1X1⊥ab；

（2）再作出D 面和△ABC 的新投影d′1 和a′1b′1c′1（为一直线）；

（3）过点d′1 向直线a′1b′1c′1 作垂线，得垂足的新投影k′1，投影d′1k′1 之长即为所求的距离。

2）点到直线的距离及其投影

【例2-3】　如图2-41（a）所示，已知线段AB 和线外一点C 的两个投影，求点C 到直线AB 的距离，并作出点C 对AB 的垂线的投影。

分析：要使新投影直接反映点C 到直线AB 的距离，过点C 对直线AB 的垂线必须平行于新投影面，即直线AB 或垂直于新的投影面，或直线AB 与点C 所决定的平面平行于新投影面。要将一般位置直线变为投影面垂直线，必须经过二次换面，因为垂直于一般位置直线的平面不可能又垂直于投影面。因此要先将一般位置直线变换为投影面平行线，再由投影面平行线变换为投影面垂直线。

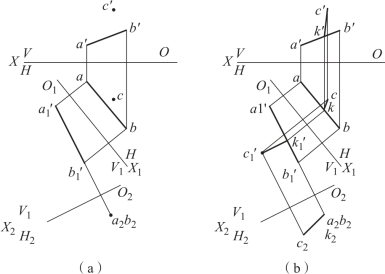
图2-41　求点到直线的距离及其投影

作图步骤：

（1）求点C 到直线AB 的距离。在图2-41（b）中先将直线AB 变换为正平线（∥V1面），再将正平线变换为铅垂线（⊥H2 面），点C 的投影也随着变换过去，线段c2k2 即等于点C 到直线AB 的距离。

（2）作出点C 对直线AB 的垂线的旧投影。如图2-41（b）所示，直线AB 的垂线CK在新投影体系V1H2 中平行于H2 面，因此CK 在V1 面上的投影c′1k′1 ∥O2X2 轴，而与c′1k′1 ⊥a′1b′1。据此，过c′1 点作O2X2 轴的平行线，就可得到k′1 点，利用直线上点的投影规律，由k′1点反向推导，在直线AB 的相应投影上，先后求得垂足K 点的两个旧投影k 点和k′点，连接c′k′、ck。c′k′、ck 即为点C 对直线AB 的垂线的旧投影。

3）交叉直线之间的距离

两交叉直线之间的距离，应该用它们的公垂线来度量。

（1）当两交叉直线中有一条直线是某一投影面的垂直线时，不必换面即可直接求出两交叉直线之间的距离；

（2）当两交叉直线中有一条直线是某一投影面的平行线段时，只需要一次换面即可求出两交叉直线之间的距离；

（3）当两交叉直线都是一般位置直线时，需要进行二次换面才能求出两交叉直线之间的距离。

【例2-4】　如图2-42 所示，已知两条交叉直线AB、CD，求两直线间的距离。

作图方法和步骤：

（1）因为AB、CD 两直线在V/H 体系中均为一般位置直线，所以需要二次换面。先用V1 面代替V 面，使V1 面∥AB，同时V1 面⊥H 面。此时AB 在新投影体系V1/H 中为投影面平行线。在新投影体系中求出AC、CD 的新投影a′1b′1、c′1d′1。

（2）在适当的位置引入新投影轴O2X2⊥a′1b′1，用H2 代替H 面，使H2 面⊥a′1b′1。

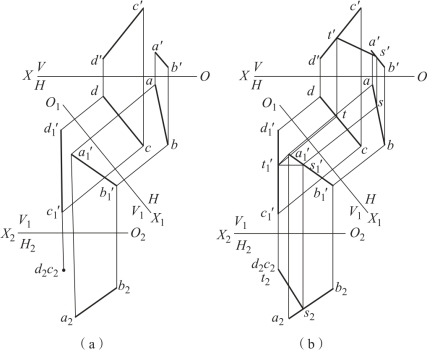
图2-42　两交叉直线之间的距离