各种位置直线的投影特性分析

按直线与三个投影面之间的相对位置，空间直线可分为两大类，即特殊位置直线和一般位置直线。特殊位置直线又分为投影面平行线和投影面垂直线。直线与投影面之间的夹角，称为直线的倾角。直线对H 面、V 面、W 面的倾角分别用希腊字母α、β、γ 表示。

1.投影面平行线

平行于一个投影面而与另外两个投影面都倾斜的直线，称为投影面平行线。投影面平行线可分为以下3 种：

（1）平行于H 面，同时倾斜于V、W 面的直线，称为水平线；

（2）平行于V 面，同时倾斜于H、W 面的直线，称为正平线；

（3）平行于W 面，同时倾斜于H、V 面的直线，称为侧平线，如表2-1 所示。

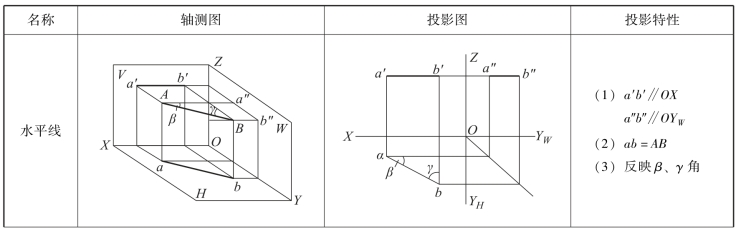
表2-1　投影面平行线投影特性

续表

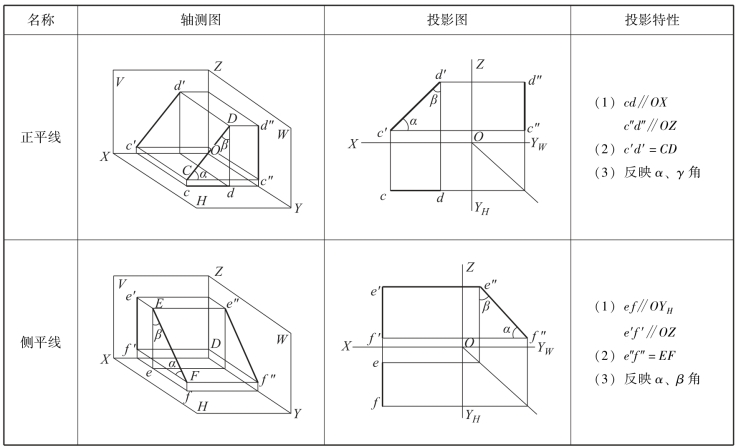
下面以水平线为例说明投影面平行线的投影特性。

在表2-1 中，由于水平线AB 平行于H 面，同时又倾斜于V、W 面，因而其H 投影ab与直线AB 平行且相等，即ab 反映直线的实长。投影ab 倾斜于OX、OYH 轴，其与OX 轴的夹角反映直线对V 面的倾角β 的实形，与OYH 轴的夹角反映直线对W 面的倾角γ 的实形，AB 的V 面投影和W 面投影分别平行于OX、OYW 轴，同时垂直于OZ 轴。同理，可得出正平线CD 和侧平线EF 的投影特性。

综合表2-1 中的水平线、正平线、侧平线的投影规律，可归纳出投影面平行线的投影特性如下：

（1）投影面平行线在它所平行的投影面上的投影反映实长，且倾斜于投影轴，该投影与相应投影轴之间的夹角，反映空间直线与另外两个投影面的倾角；

（2）其余两个投影平行于相应的投影轴，长度小于实长。

2.投影面垂直线

垂直于一个投影面的直线称为投影面垂直线，它分为3 种：

（1）垂直于H 面的直线，称为铅垂线；

（2）垂直于V 面的直线，称为正垂线；

（3）垂直于W 面的直线，称为侧垂线，如表2-2 所示。

下面以铅垂线为例说明投影面垂直线的投影特性。

在表2-2 中，因直线AB 垂直于H 面，所以AB 的H 投影积聚为一点a（b）；AB 垂直于H 面的同时必定平行于V 面和W 面，所以由平行投影的显实性可知：a′b′=a″b″=AB，并且a′b′ 垂直于OX 轴，a″b″垂直于OYW轴，它们同时平行于OZ 轴。(www.xing528.com)

表2-2　投影面垂直线投影特性

综合表2-2 中的铅垂线、正垂线、侧垂线的投影规律，可归纳出投影面垂直线的投影特性如下：

（1）直线在它所垂直的投影面上的投影积聚为一点；

（2）直线的另外两个投影平行于相应的投影轴，且反映实长。

【例2-1】　已知直线AB 的水平投影ab，AB 对H 面的倾角为30°，端点A 距水平面的距离为10，A 点在B 点的左下方，如图2-12（a）所示，求AB 的正面投影a′b′。

图2-12　作正平线的V 面投影

解：

1）作图分析

由已知条件可知，AB 的水平投影ab 平行于OX 轴，因而AB 是正平线，正平线的正面投影与OX 轴的夹角反映直线与H 面的倾角。A 点到水平面的距离等于其正面投影a′到OX轴的距离，从而先求出a′。

2）作图步骤

（1）过a 作OX 轴的垂线aax，在aax 的延长线上截取a′ax=10，如图2-12（b）所示。

（2）过a′作与OX 轴成30°的直线，与过b 所作的OX 轴垂线bbx 的延长线相交，因A 点在B 点的左下方，故所得交点即为b′，连接a′b′即为所求，如图2-12（c）所示。

3.一般位置直线

与3 个投影面都倾斜（既不平行又不垂直）的直线称为一般位置直线，简称一般线。

从图2-13 中可以看出，一般位置直线具有以下投影特性：

（1）直线在3 个投影面上的投影都倾斜于投影轴，其投影与相应投影轴的夹角不能反映其与相应投影面的真实的倾角；

（2）3 个投影的长度都小于实长。

图2-13　一般位置直线