1.等分直线段
过已知线段的一个端点,画任意角度的直线,并用分规自线段的起点量取n 个线段。将等分的最末点与已知线段的另一端点相连,再过各等分点作该线的平行线,与已知线段相交即得到等分点,如图1-24 所示。
作法:(1)过端点A 任作一直线AC,用分规以等距离在AC 上量取1、2、3、4、5各点;
(2)连接5B,过1、2、3、4 作5B 的平行线与AB 相交,得等分点1′、2′、3′、4′,即为所求。
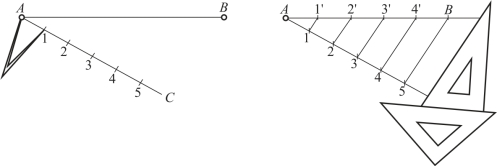
图1-24 等分直线段
2.等分圆周
下面介绍圆内接正五边形、正六边形的作法;并以正七边形为例,介绍圆内接正n 边形的近似作法。
1)正五边形(如图1-25 所示)
(1)作OA 的中点M;
(2)以M 点为圆心,M1 为半径作弧,交水平直径于K 点;
(3)以1K 为边长,将圆周5 等分,即可作出圆内接正五边形。(https://www.xing528.com)
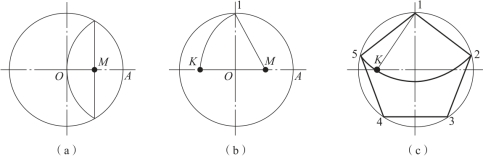
图1-25 正五边形画法
2)正六边形(如图1-26 所示)
正六边形的画法分为圆规作图和三角板作图两种。
(1)用圆规作图:分别以已知圆在水平直径上的两处交点A、O 为圆心,以R=AD/2作圆弧,与圆交于B、C、E、F 点,依次连接A、B、C、D、E、F 点,即得圆内接正六边形,如图1-26(a)所示。
(2)用三角板作图:以60°三角板配合丁字尺作平行线,画出4 条斜边,再以丁字尺作上、下水平边,即得圆内接正六边形,如图1-26(b)所示。
3)正n 边形(如图1-27 所示)
n 等分铅垂直径AK(在图中n=7),以A 点为圆心,AK 为半径作弧,交水平中心线于点S,延长连线S2、S4、S6…,与圆周交得点G、F、E…,再作出它们关于AK 的对称点,即可作出圆内接正n 边形。

图1-26 正六边形画法

图1-27 正n 边形画法
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




