锥台体的三视图及图示特点详解

1.锥台体的视图选择

根据物体上有尽可能多的表面平行或垂直于投影面的投影原则，锥台体在三投影面体系中放置的位置，一般为底面（上、下底面）平行于某个投影面。正六棱锥、圆锥、混合锥的三视图，如图3-17所示；台体的三视图，如图3-18所示。

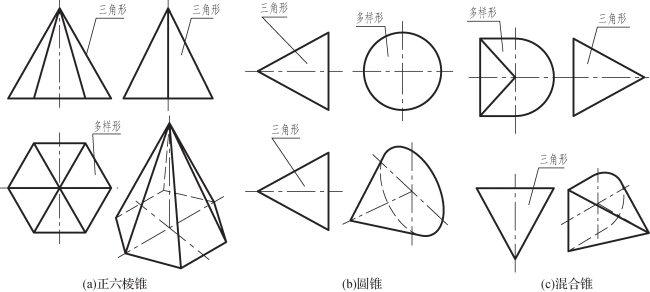
图3-17　锥体的三视图

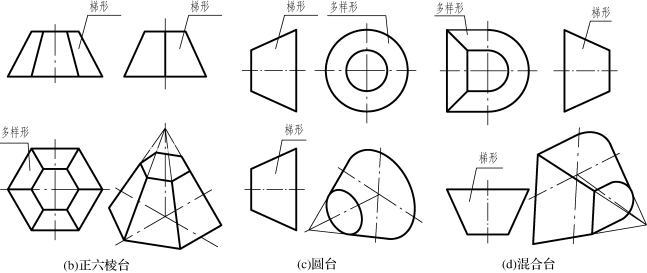
图3-18　台体三视图

2.锥体、台体三视图的图示特征(www.xing528.com)

（1）锥体三视图的图示特征

在锥体的三个视图中，有两个视图的外轮廓是三角形，此三角形由公共顶点的n（n=1～∞）个小三角形组成，我们将这两个图形概括简称为“三角形”；而第三视图的外轮廓是一个有多种样式的封闭图形，它是锥体底面的真实性的投影，也是锥体的特征形状。该封闭图形则是由一个公共顶点的n（n=1～∞）个小三角形组成（圆锥可以看成n=∞，而省略不画）。这n个小三角形均是锥体侧面的类似性投影。就是这样一个第三个图形，我们将它概括简称为“多样形”。这样，锥体三视图的图示特征就可概括为：“一多样形、两三角形”，如图3-17所示。

（2）台体三视图的图示特征

在台体的三个视图中，有两个图形的外轮廓是梯形，它是由n（n=1～∞）个同高梯形组成。而第三个图形的外轮廓则是一个多种样式的封闭图形（即多样形），它由大、小两个相似图形或类似图形及两个相似图形或类似图形之间围绕着n（n=1～∞）个小梯形组成。这n个小梯形都是台体侧面的类似性投影。大小两个相似图形或类似图形即为台体的下底面和上底面的真实性投影，是台体的特征形状。这个第三个图形，我们简称为“多样形”。

同样，圆台的侧面应视作为由n（正多边形的边数）趋向于无穷多时，这些小梯形的极限就是连续、光滑的圆台面，它的外轮廓就由大、小两个圆组成了一个“多样形”，

综上所述，用“一多样形、两个梯形”（又简称为“一多样、两梯形”）即可概括出台体三视图的图示特征，如图3-18所示。