光电效应：外与内的区别

光照射在半导体材料上，材料的电学性质发生了变化（电导率改变、发射电子、产生感应电动势）的现象，称为光电效应。光电效应可分为外光电效应和内光电效应两大类。外光电效应是指受到光辐射后，产生电子发射的现象；内光电效应是指受到光照射的物质内部电子能量状态产生变化，但不存在表面发射电子的现象。

1.外光电效应（光电子发射） 这是指受到光辐射后，产生电子发射的现象。具有外光电效应的材料称为光电子发射体。光电子发射包括了三个过程：光子被材料吸收、光电子向材料表面运动，以及光电子逸出界面。

（1）光子被材料吸收。光照到物质时，存在五种不同的吸收过程：本征吸收、晶格振动吸收、自由载流子吸收、激子吸收、杂质吸收。不论哪种吸收，电子被激发后的能量必须高于真空能级E₀才有可能逸出表面。半导体材料的本征吸收系数很高，可达10⁵cm^-1，因而由本征半导体吸收光子而产生光电子的量子效率很高，可达30%，这种光电子发射体称为本征发射体；如果主要是杂质吸收造成的光电子发射，则称为杂质发射体，但杂质含量一般较低，只占本征材料的1/100以下，产生光电子的量子效率远低于本征材料吸收光子所产生的效果。其他类型的光吸收，由于在半导体中含量更低，所产生的光电子已没有实际意义。本征发射体主要材料有锑、铯光电阴极，锑、钾、钠、铯等。

（2）光电子向材料表面运动。光子照射到特质表面要渗透到一定的深度，才能保证光电子有足够的能量克服损耗，到达表面。损耗有晶格散射损耗和与价带电子碰撞损耗，晶格散射损耗能量只有零点几电子伏特，与导带底部有几个电子伏特状态相比，还是很小的；与价带电子碰撞的损耗较大，有可能产生二次电子发射，消耗的能量约为禁带宽度的2～3倍。

（3）光电子逸出界面。光电子到达表面后能否逸出，要看电子剩余的能量是否大于表面势能，这个能量称为电子亲和势χ，它表征了材料的一种特性，其计算公式如下：

χ=E₀-E_C （2-61）

另一种表征材料特性的量为逸出功，与费密能级E_F有关。由于费密能级E_F的位置随着对材料的掺杂不同而不同，因而逸出功有某种程度的不确定性，所以经常使用电子亲和势来讨论光电发射的问题。

图2-19 光电子发射

1）电子逸出条件。从式（2-61）可以看出，χ值低，电子容易逸出。要使χ值低，真空能级E₀就要低。材料边界条件不同，可使能带发生弯曲，虽然禁带宽度并不发生变化，导带底与价带顶的能量值改变，电子亲和势χ发生改变，或是χ+Δχ，或是χ-Δχ。可以通过选择适当的材料及表面吸附物质，使能带向下弯曲，实现真空能级E₀降低，光电逸出功也就相应降低了。当E₀降到比E_C还要低时，入射光子的能量仅需等于或稍大于禁带宽度，就可以产生光电子发射，相应地入射光子的透入深度可大大增加，比一般光电阴极的透入深度要大1～3个数量级，极大地提高了光电阴极的量子效率。E₀﹥E_C的材料称为正电子亲和光电阴极，E₀﹤E_C的材料称为负电子亲和势的光电阴极。重掺杂的p型材料是实现负电子亲和势的最好选择。图2-19所示为光电子发射。

2）电子逸出遵守的定律。电子逸出即光电发射，是光能转变为电能的一种形式，遵守爱因斯坦定律和斯托列托夫定律。

①爱因斯坦定律

式中 v_max———光电子逸出材料后具有的最大速度；

W———材料的逸出功。

式（2-62）表明，只有h_ν﹥W，才可能产生光电发射。因此入射光频率有一个下限值，称为红限频率，相应的波长称为红限波长（长波限）。

②斯托列托夫定律

I_K=S_KΦ_V （2-63）

式中 I_K———饱和光电流；

S_K———比例常数，称为光电发射体的灵敏度（A/lm）；

Φ_V———入射光通量。

式（2-63）说明，光电流的大小是与入射光强度成正比的。只有入射光频率高于红限值的前提下，光电流才可能产生，且遵循式（2-63）关系。

有光电子发射效应的材料，主要响应在可见光波段（0.38～0.76μm），红外波段（0.76～1000um）的响应灵敏度较低。

2.内光电效应（光电导效应与光伏效应）

（1）光电导效应。光吸收使半导体中形成非平衡载流子，而载流子浓度的增大必然使电导率增大，这种由光照引起半导体电导率增加的现象称为光电导。本征吸收引起的光电导称为本征光电导。

1）附加电导率Δσ，即有光照时电导率的增量。

无光照时，半导体电导率应为

σ₀=e（n₀μ_N+p₀μ_P） （2-64）

式中 σ₀———半导体电导率，一般称暗电导；

e———电子电荷；

n₀———电子浓度；

μ_N———电子迁移率；

p₀———空穴浓度；

μ_P———空穴迁移率。

有光照时光注入，电子浓度增量为Δn₀，空穴浓度增量为Δp₀。当电子刚被激发到导带时，可能比原来在导带中的热平衡电子有较大的能量，但光生电子通过与晶格碰撞，在极短的时间内就以发射声子的形式丢失多余的能量，变成热平衡电子。因此，可以认为在整个光电导过程中，光生电子与热平衡电子具有相等的迁移率，因而在光照下的电导率变为

σ₀=e[（n₀+Δn）μ_N+（p₀+Δp）μ_P]

附加电导率Δσ为

Δσ=e（Δnμ_N+Δpμ_P）

实验证明两点：在许多半导体材料的本征吸收中，Δn=Δp；并不是光生电子和光生空穴都对光电导有贡献，虽然在本征光电导中光激发的电子和空穴数是相等的，但在它们复合消失以前，只有其中一种光生载流子（一般是多数载流子）较长时间存在于自由状态，而另一种则被一些能级（陷阱）束缚住，这样导致Δn﹥﹥Δp或者Δp﹥﹥Δn，从而得出

Δσ=eΔnμ_N （2-65）

或 Δσ=eΔpμ_P

2）定态光电导及光电导弛豫

①定态光电导。在恒定光照下产生的光电导称定态光电导。研究光电导主要是研究光照下半导体附加电导率Δσ的变化规律。根据式（2-65），因为μ_N、μ_P在一定条件下是一定的，所以Δσ的变化反映了光生载流子Δn或Δp的变化。

电子-空穴对的产生率可写为

Q=βIα （2-66）

式中 β———每吸收一个光子产生的电子-空穴对数，称为量子产额，每吸收一个光子产生一个电子-空穴对，则β=1，但当光子还由于其他原因被吸收，如形成激子等，则β﹤1。

I———以光子数计算的光强度，即单位时间通过单位面积的光子数。

α———样品吸收系数。

设在某一时刻开始，以强度I的光照射半导体表面，假设除激发过程外，不存在其他任何过程，则经t秒后，光生载流子的浓度为

Δn=Δp=βIαt （2-67）

如光照保持不变，光生载流子浓度将随时间t线性增大。图2-20示出光生载流子浓度变化。理论上的变化如图中虚线所示。但事实上，由于光激发的同时，还存在复合过程，因此Δn、Δp不可能直线上升，而是如图中曲线所示，最后达到一稳定值Δn_s，这时附加电导率Δσ也达到稳定值Δσ_s。这就是定态光电导。达到定态光电导时，电子-空穴的复合率等于产生率，即R=Q。

图2-20 光生载流子浓度变化

②光电导弛豫。在光照下光电导逐渐上升和光照停止后光电导逐渐下降的现象，称为光电导弛豫。

设光生电子寿命为τ_n、光生空穴的寿命为τ_p，根据式（2-67）得光生载流子浓度为

Δn_s=βIατ_n，Δn_p=βIατ_p（2-68）

从而定态光电导率为

Δσ_s=eβIα（μ_nτ_n+μ_nτ_p）（2-69）

式中 β———量子产额；

I———光强度；

α———样品吸收系数；

μ_n———电子迁移率；

μ_p———空穴迁移率。(www.xing528.com)

其中，β、α表征光和物质的相互作用，决定光生载流子的激发过程；τ、μ表征载流子和物质的相互作用，决定载流子运动和非平衡载流子的复合过程。

光照后经过一定的时间才到达定态光电导率Δσ_s；同样，当光照停止后，光电导率也会逐渐地消失。图2-21示出光电导弛豫过程。

图2-21 光电导弛豫过程

下面讨论弛豫过程中，光生载流子浓度（光电导率）与光照时间的关系。为了简化过程，假定一种载流子起作用，令Δp≈0，分光小量注入与光强量注入两种情况：

a）光小量注入时，光生载流子寿命τ是定值，复合率R等于Δn/τ，设t=0时开始光照，光强度为I，在光照中，Δn的增加率为

分离变量并积分，利用起始条件t=0，Δn=0，解方程得

当t﹥﹥τ时 Δn=βαIτ=Δn_s

式中 Δn_s———光生载流子的定态值。

光照停止后，Q=0，光生载流子的下降方程为

设t=0时停止光照，这时光生载流子浓度已达到定态值，即t=0时，Δn=Δn_s，解式（2-72），得

由式（2-69）Δσ_s=eβIα（μ_nτ_n+μ_nτ_p），设Δp≈0，可得下降附加电导率Δσ为

同理可得上升附加电导率Δσ为

τ通常称为弛豫时间。式（2-74）和式（2-75）曲线见图2-21的光电导弛豫过程。

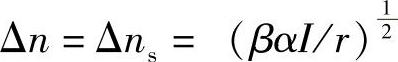b）光强量注入时，非平衡载流子（电子）浓度Δn﹥﹥n₀、p₀（平衡载流子电子、空穴浓度），载流子寿命τ不再是定值，式（2-70）中的复合率改为r（Δn）2，r为比例系数，称为电子-空穴复合概率。它仅是温度的函数，而与n、p无关。上升时下降时初始条件：上升时t=0，Δn=0；下降时t=0，。这样就可列出光强量注入下Δn的弛豫方程为上升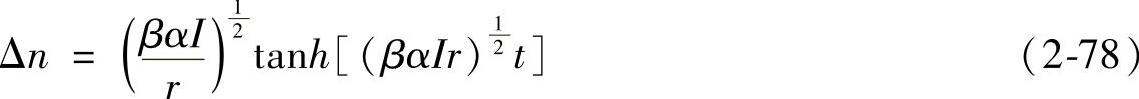时下降时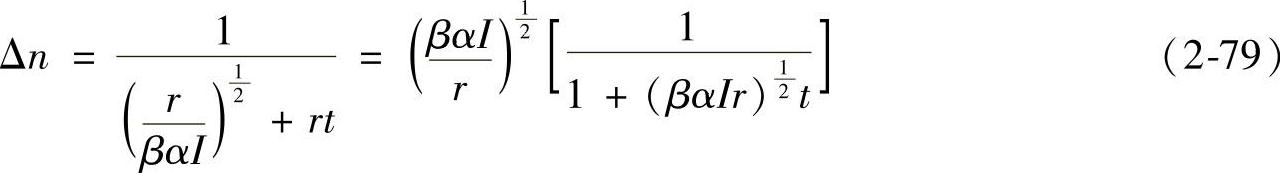

在光强量注入情况下，光电导弛豫过程比较复杂，寿命不再是定值，而是光照强度和时间的函数，即τ=f（I，t）。

3）光电导灵敏度及光电导增益

① 光电导灵敏度定义为单位光照度所引起的光电导Δσ_s（Δn_s）。在一定光照下Δσ_s（Δn_s）越大，其灵敏度越高。

② 光电导增益。将某种材料制成的光敏电阻两端接上电源，在外加电场作用下，光生载流子（设为电子）在两电极间的定向运动，形成电路中的光电流。当一个电子在电场作用下到达正电极时，负电极必须同时释放出一个电子，以保持光敏电阻的电中性，这种过程一直继续到光生载流子复合的发生。在一定条件下，光生电子寿命τ_n可以大大超过电子从一个电极漂移到另一个电极所需时间τ_t。这样，光敏电阻每吸收一个光子，就能使许多个电子相继通过两个电极，电极较靠近时的光电流将大于电极远离时的光电流，这就是光电导增益，用符号G表示，即

G=τ_n/τ_t

如外加电压为V，电子迁移率为_μn，电极间距离为l，则渡越时间为

则光电导增益为

对寿命长、迁移率大的材料，在两极很靠近的情况下，光电导增益G可以很大。如果材料有陷阱中心存在时，载流子寿命增大，G可以达到10³，但响应速度下降。

4）复合和陷阱效应对光电导的影响。杂质能级积累非平衡载流子的作用称为陷阱效应。有显著陷阱效应的杂质能级称为陷阱，而把相应的杂质和缺陷称为陷阱中心。

前面讨论光电导机理，是基于以下几种情况：光在小注入情况下、复合中心陷阱作用忽略，两种非平衡载流子相等，即Δn=Δp。Δn、Δp是和平衡载流子Δn₀、Δp₀作为比较标准的，对高阻材料，Δn₀、Δp₀很小。实际情况不是这样，光强不限于小注入，杂质含量可比平衡载流子浓度大许多倍，往往会发生十分强烈的陷阱作用。如只有一种复合中心决定光电导的过程，非平衡少数载流子大部分时间被陷在复合中心，等待与自由的多数载流子复合。但是实验证明，半导体材料除了复合中心外，还存在浓度相当高的、主要起陷阱作用中心，因而，少数载流子陷阱有增加定态光电导灵敏度的作用。在光电材料中有时加入适当杂质，可提高灵敏度。多数载流子陷阱增长了光电导上升、下降的弛豫过程，其影响的程度决定于陷阱深度。

5）本征光电导的光谱分布。光电导的光谱分布，是指对应于不同的波长，光电导响应灵敏度的变化关系。光电导的强弱与照射光的波长有密切关系。一般以波长为横坐标，以相等的入射光能量，或相等的入射光子数，所引起的光电导相对大小为纵坐标，就得到光电导光谱分布曲线。本征光电导的光谱分布都有一外长波限，有时也称为“截止”波长。这是由于能量小的光子，不足使价带电子跃迁到导带，因而不能引起光电导。一般选定光电导下降到峰值的1/2的波长为长波限。在光谱曲线中，不同波长所用的光强标准不同，有“等量子”和“等能量”的区别。“等量子”是指对于不同的波长，以光子数计的光强是相同的。“等能量”是指不同波长光强的能量流是相同的。光电导是光子吸收的直接效应，所以测量光电导时，采用“等量子”光照强度较合适。

测量光电导的光谱分布，是确定半导体材料光电导特性的一个重要方面，对选用材料有实际意义。

6）杂质光电导。光照使束缚于杂质半导体能级上的电子可空穴电离，因而增加了导带或价带的载流子浓度，产生杂质光电导。由于杂质电离能比禁带宽度E_g小很多，因此从杂质能级上激发电子或空穴所需的光子能量比较小。杂质半导体原子浓度比半导体材料本身的原子浓度一般要小很多个数量级，所以和本征光电导相比，杂质光电导是十分微弱。所涉及的能量都在红外光范围，激发光实际上不可能很强，测量杂质光电导一般都要在低温下进行，以保证平衡载流子浓度（暗电导）很小，使杂质中心上的电子或空穴基本上都处在束缚状态。

（2）光伏效应。当用适当波长的光照射非均匀半导体p-n结时，不加外电场，由于内建场的作用，半导体内部产生电动势（光生电压），如将p-n结短路，则会出现电流（光生电流）。这种由内电场引起的光电效应，称为光伏效应（光生伏特效应）。

1）p-n结的光伏效应。由p型半导体和n型半导体结合，结合面产生p-n结。在没有光照的情况下，由于p区空穴浓度比n区空穴浓度大，n区电子浓度比p区电子浓度大，产生了浓度梯度，从而在材料内部出现了内电场，方向由n区指向P区，形成势垒eV_D，阻止空穴和电子进一步移动，达到平衡状态。当入射光垂直照射p-n结面，光子进入p-n结区，能量大于禁带宽度的光子，经本征吸收，在p-n结的两边产生电子-空穴对，打破原有的平衡。由于p-n结存在内电场，结两边的光生少数载流子在该电场作用下，各自向相反方向运动：p区的电子穿过p-n结进入n区，n区的空穴进入p区，使p端电势升高，n端电势降低，在p-n结两端形成了光生电动势，这就是光生伏特效应，简称光伏效应。光生电动势相当于在p-n结两端加正向电压V，使势垒降低为eV_D-eV，产生正向电流I_F。在p-n结开路情况下，光生电流和正向电流相等时，p-n结两端建立起稳定的电势差V_oc（P区相对N区是正的），这就是光电池的开路电压。如将p-n结与外电路接通，外接负载形成回路，只要光照不停止，就会有源源不断的电流通过电路，方向由n区指向p区，p-n结起了电源的作用，若负载为0，测出的电流就是短路电流。这就是光电池-光电二极管的基本原理，太阳电池是典型的光电池。

2）光电池的电流电压特性。光电池工作时有三股电流：光生电流I_L、正向电流I_F、外电路电流I₀。I_L及I_F都流经p-n结内部，但方向相反。

①光生电流I_L。光照射光电池，因存在吸收，光强度随着光透入的深度按指数律下降，因而光生载流子产生率也随光照深入而减小，即产生率Q是x的函数。光生电流I_L为

式中 e———电子电量；

Q———结的扩散长度（L_P+L_n）内非平衡载流子的平均产生率，并假定扩散长度L_P内的空穴和L_n内的电子都能扩散到p-n结而进入另一边；

A———p_-n结面积。

光生电流I_L从n区流向p区，与I_F相反。

②正向电流I_F。根据p-n结整流方程，在正向偏压V作用下，通过结的正向电流为

式中 I_s———反向饱和电流；

V———光生电压。

3）外电路电流I₀。光电池与负载接成通路，通过负载的电流为

这就是负载电阻上电流与电压的关系，也就是光电池的伏安特性。图2-22所示为光电池的伏安特性。

从式（2-82）可得

在负载电阻R→∞，p-n结开路，两端电压为开路电压V_oc，这时流经负载电阻R电流I₀=0，即I_L=I_F，代入式（2-83），得开路电压为

将p-n结短路，光生电压V=0，正向电流I_F=0，所得电流为短路电流I_sc，由式（2-82）得I_sc=I_L。

图2-22 光电池的伏安特性

V_oc和I_sc是光电池的两个重要参数，其数值可由图2-22，光电池的伏安特性曲线2在V轴和I轴上的截距求得。从各自表达式（2-81）和式（2-84）可看出，两者都随光照强度的增强而增大，I_sc随光照强度线性地上升，V_oc成对数式增大。图2-23示出V_oc和I_sc随光强度变化。

要注意V_oc并不随光照强度无限地增大，当光生电压V_oc增大到p-n结势垒消失时，即得到最大光生电压V_max，因此V_max应等于p-n结势垒高度V_D，与材料掺杂程度有关。实际上V_max与禁带宽度E_g相当。

3.光电效应和波动理论的矛盾

（1）按照光的电磁理论可以预测。光越强，电子接受的能量越多，释放出去的电子的动能也越大；释放电子主要决定于光强度，应当与频率等没有关系。

但是，试验测量的结果却并不如此。试验现象如下：

1）在入射光的强度与频率不变的情况下，当加速电压V增加到一定值时，光电流达到饱和值。

图2-23V_oc和I_sc随光强度变化

2）当电位差V减小到零，并逐渐变负时，光电流并不降为零。这表明从电极K逸出的光电子具有初动能。

3）用不同频率的光去照射光电子时，试验结果是频率越高，V_oc越大，并且与V_oc成直线关系。频率低的光，不论强度多大，都不能产生光电子，因此，V_oc称为阈频率。对于不同的材料，阈频率不同。

（2）规律

1）饱和电流I的大小与入射光的强度成正比，即单位时间内被击出的光电子数目与入射光的强度成正比。

2）光电子的最大初动能（或遏止电压）与入射光的强度无关，而只与入射光的频率有关。频率越大，光电子的能量就越大。

3）入射光的频率低于遏止频率的光，不论光的强度如何，照射时间多长，都没有光电子发射。

4）光的照射和光电子的释放几乎是同时的，在测量的精度范围内（10^-9s），观察不出这两者间存在滞后现象。