光的波粒二象性及其偏振态

1.单色光 具有确定频率的光称为单色光，它所占据的光谱宽度等于零。单色光仅是一种理想模型，实际光波总占据某一有限的光谱宽度。

2.光矢量E 光是一种电磁波，由电场强度E和磁场强度H组成。在光与物质相互作用中，电场起主要作用，故通常将E称为光矢量。

3.偏振态 两列同频率平面波的叠加结果与两波的振动方向直接有关。当两列波的振动方向相同时，合成波光矢量仍作同方向的振动；当两列波的振动方向垂直时，合成波光矢量一般要作椭圆振动。光的横波性只规定了光矢量E位于与传播方向垂直的平面内，并未限定E在该平面内的具体振动方式，这种具体振动方式（振幅与相位随方位的分布）称为光的偏振结构或光的偏振态。

光的偏振态可以分为三类：完全偏振光、非偏振光即自然光及部分偏振光。

（1）完全偏振光。光的传播方向为z轴正向，E位于xy平面。根据正交分解法，任何形式的光振动总可以分解为x、y方向的分振动E_x、E_y。如果这两个分振动完全相关，即有完全确定的相位关系，则相应的光称为完全偏振光，简称偏振光。完全偏振光有三种基态：线偏振光、圆偏振光和椭圆偏振光。

1）线偏振光。光矢量E的振动方位保持不变的光，称为线偏振光。若固定某一位置观察光矢量的时间变化。则其末端在xy平面上扫描出一个方位确定的线段；若固定某一时刻考察光矢量的空间变化，则各处光矢量位于一个取向确定的平面，即E与光的传播方向构成的平面内，此平面称为振动面。

2）圆偏振光。在任一位置光矢量E的末端随时间变化，在xy平面上扫描出一个圆的光，称为圆偏振光。根据E的旋向可以进一步分为左旋圆偏振光和右旋圆偏振光。

3）椭圆偏振光。在任一位置光矢量E的末端随时间变化，在xy平面上扫描出一个椭圆的光，称为椭圆偏振光。根据E的旋向亦可以进一步分为左旋椭圆偏振光和右旋椭圆偏振光。

（2）非偏振光即自然光。两个振动方向相互垂直，振幅可强度相等、相互独立的线偏振光，称为非偏振光或自然光。

（3）部分偏振光。许多实际问题中，光波既不是完全偏振光，也不是自然光，而是两者的混合，这种光称为部分偏振光。

4.起偏器 能够使自然光变成某种偏振光的光学器件，称为起偏器。根据输出光的偏振形态，可以把起偏器分为线起偏器、圆起偏器等。各种起偏器的作用过程都必须包含某种不对称性，它可以是介质在不同作用条件（如不同的入射角）下的不同响应，更多的是介质本身的各向异性。

5.光的干涉 若在两波交叠区，波场的强度分布不是简单地等于每列单独产生的强度之和，即

I（P）≠I₁（P）+I₂（P） （2-5）则称这两列波发生了干涉。两列波相干条件如下：

1）频率相同。

2）振动方向不相互正交。

3）相位差恒定（不随时间而变化）。

6.光的衍射 波在传播过程中遇到障碍物时，偏离几何光学路径的现象称为波的衍射。

7.光栅 广义上可以对入射光的振幅或相位作周期性空间调制的任何装置均可称为光栅。光栅有三个基本参数：缝宽a、缝距d及总缝数N。

光栅按调制量是入射光的振幅还是相位，可分为振幅光栅和相位光栅；按工作方式可分为透射光栅和反射光栅；按结构可分为平面光栅和立体（三维）光栅。

8.光的色散 介质折射率随光的频率或波长而变化的现象称为色散。

9.光的散射 光束通过光学性质不均匀的介质时，从侧向可观察到光，这种现象称为光的散射。

光的散射原因：在入射光作用下，介质分子（原子）或其中的杂质微粒可看作是次波源而辐射次波。对完全纯净均匀的介质，各次波相干叠加的结果，使得只在原入射光方向发生干涉相长，其他方向均干涉相消，故光线按几何光学所确定的方向传播。在介质不均匀时，各次波的相位无规性，使得最终的叠加结果呈非相干性，即除原入射光方向之外，其他方向亦有光强分布，散射现象也就出现了。

光散射的过程是光与介质中分子（原子）作用而改变其光强的空间分布、偏振态或频率的过程。按散射光频率与入射光频率相比是否改变，可分成两大类：频率不变的散射有瑞利散射、米氏散射、大粒子散射；频率改变的有拉曼散射。

10.谱线 频率范围很窄的辐射场的抽样，从外形上看，谱线可以被认为是由阻尼（基本的）振荡器产生的辐射。

11.信噪比 这是指放大器的输出信号的电压与同时输出的噪声电压比，常常用分贝数表示。设备的信噪比越高，表明它产生的杂音越小。信噪比一般不低于70dB。

12.光电探测器 这是将光信号转变为实时的电信号的器件。按结构可分为光电二极管、PIN光电二极管、雪崩光电二极管等。光电探测器工作原理是基于光电效应。光电探测器分为光子探测器和热探测器两大类。

13.菲涅耳反射系数公式 设介质1和介质2皆为各向同性均匀透明介质，其界面为平面。单色平面波从介质1（折射率为n₁）射向介质2（折射率为n₂）。

TE波中各量的正向规定如图2-3所示。设入射光矢量为振动矢量，为电磁波。电磁波中的电场强度矢量为E，磁场强度矢量为H，前进方向为k。以入射面为基准，任一振动矢量可以分解为两个方向正交的振动分量。其中一个振动方向垂直于放射面，另一个振动方向在入射面之内。前者称为S振动或S态，后者称为P振动或P态。因电磁波是横波，满足E×H=S。若E和H中一个为S态，另一个必为P态，例如E为S态，H为P态的波，称为横向电偏振，记为TE波；H为S态，E为P态的波，称为横向磁偏振，记为TM波。这样，任一偏振态的入射光均可按正交分解法，看作是TE波和TM波这两种线偏振光的叠加。根据E和H的切向分量在界面连续的条件，以及入射波、界面及两侧介质关于入射面的空间对称性，可以判定当入射波中E为S态，H为P态时，反射波及折射波中E也为S态，H也为P态。为了表述方便，对S、P态振动的正方向作一规定，取S态正向为垂直于入射面（即纸面）向外，P态的正向依据E、H、k依其顺序组成右手正交系来确定。

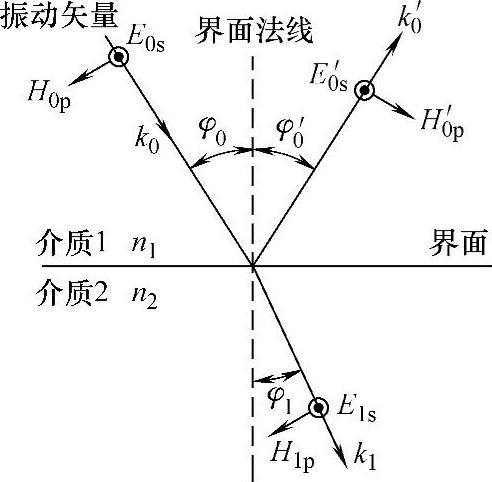
图2-3TE波中各量的正向规定

1）对于TE波，按图2-3TE波中各量的正向规定。标记0、0′及1，分别表示入射光、反射光和折射光，各量都对界面上同一点而言。由切向分量连续的边界条件，可以得

E_0s+E₀′_s=E_1s （2-6）

-H_0pcosφ₀+H₀′_pcosφ₀=-H_1pcosφ₁ （2-7）

式中 φ₀———入射角；

φ₁———折射角。

在光学波段，一般介质均可看作非磁介质，即可认为_μ0=μ₀′=μ₁。

由电磁理论可得

将式（2-8）代入式（2-7）中，得

n₁（E_0s-E₀′_s）cosφ₀=n₂E_1scosφ₁ （2-9）

联立式（2-6）和式（2-9），可解得

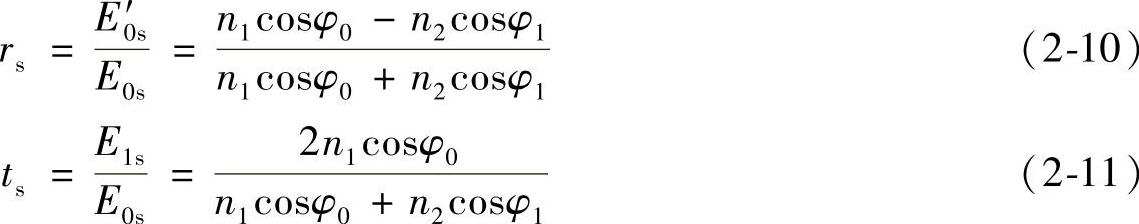
式中 r_s———S光的振幅反射率，它表示界面上反射波中E矢量的S分量的振幅与入射波中

E矢量的S分量的振幅之比；

t_s———S光的振幅透射率，它表示界面上透射波中E矢量的S分量的振幅与入射波中

E矢量的S分量的振幅之比。

2）对TM波，各量的正向规定如图2-4所示。利用完全类似的方法，可导出

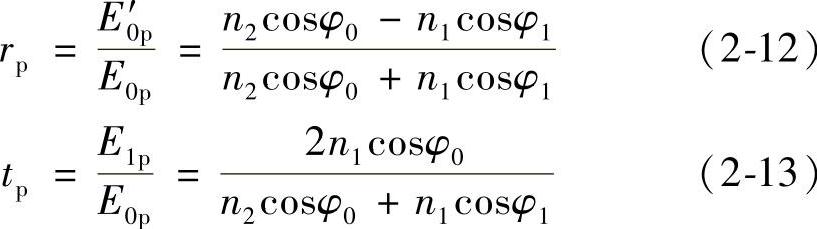
式中 r_p———P光的振幅反射率，表示界面上反射波中E

矢量的P分量的振幅与入射波中E矢量的P

分量的振幅之比；

t_p———P光的振幅透射率，它表示界面上透射波中

E矢量的P分量的振幅与入射波中E矢量的

P分量的振幅之比。

式（2-10）至式（2-13）称为菲涅耳公式。

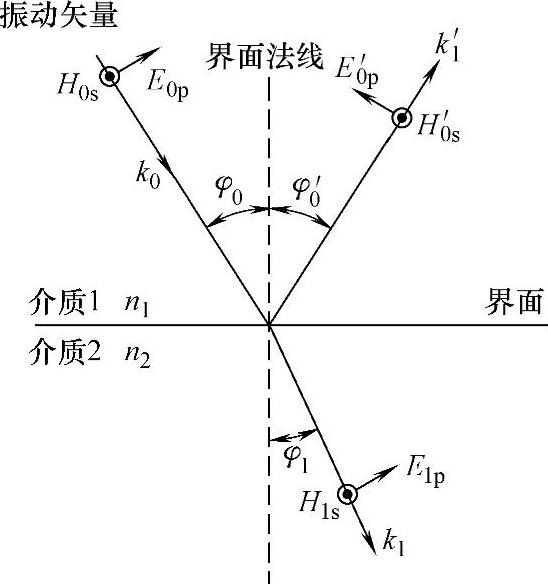
图2-4TM波中各量的正向规定

说明：

①E_s、E_p是同一矢量E的S分量和P分量，它们具有相同的时间频率。式中各个E_s、E_p既可看作是复振幅，也可以看作是瞬时值。

②在不同的正向规定下，某些公式的符号可能有所变化，但这种正向规定不应也不会影响问题的物理实质。若在某种正向规定下求得某个量是正值，表明该分量的实际方向与所规定的正向相同，负值则表示相反。

③反射波及透射波的S分量只与入射波的S分量有关，反射波及透射波的P分量只与入射波的P分量有关，即S态线偏振光与P态线偏振光是互相独立的。

14.周期厚度 用椭偏仪测量膜厚会涉及薄膜周期厚度的概念。第一个周期厚度d₀为

式中 λ———入射的氦氖激光在真空中的波长；

n₀———空气折射率；

n₁———介质膜的折射率；

φ₁———入射角。

薄膜总厚度D为

D=（j-1）d₀+d （2-15）

式中 j———周期数，用干涉法或用椭偏仪试测法可得出；

d———一个周期厚度内的某一厚度，可查表。

15.复数

（1）复数的概念。i是方程x²+1=0的一个根，即i²+1=0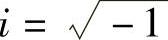，。对于任意二实数x、y，称z=x+iy或z=x+yi为复数，其中x、y分别称为z的实部和虚部，记为x=Re（z），y=Im（z），而i称为虚单位。当x=0时，z=iy称为纯虚数；当y=0时，z=x+0i称为实数x。两个复数相等，它们的实部和虚部必须分别相等。两个复数不能比较大小。

实部相等而虚部正、负号相反的两个复数称为共轭复数。如果z=x+iy，则z=x-iy。

共轭复数有如下性质：

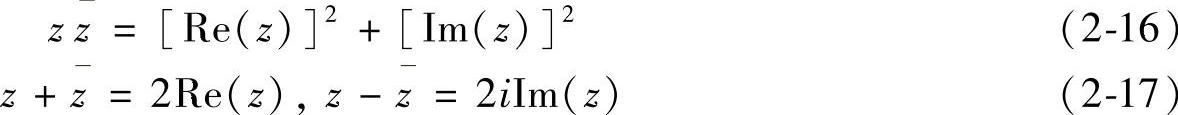
（2）复数的几何表示

1）复平面表示。复数z=x+iy轴可以用坐标为（x、y）的点表示，这是一个常用的方法。x轴称为实轴，y轴称为虚轴，两轴所在的平面称为复平面或z平面。这样，复数与复平面上的点一一对应，并且常把“点z”作为“数z”的同义词。

2）向量表示。复数z能用从原点指向点（x、y）的向量来表示。复数的向量表示如图2-5所示。向量的长度称为z的模或绝对值，记作

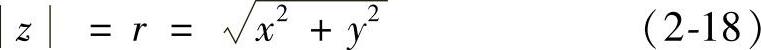(www.xing528.com)

在z≠0的情况，表示z的向量与x轴的交角θ称为z的辐角，记作

Argz=θ

这时

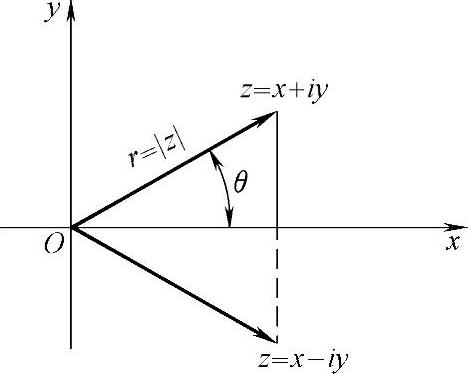
图2-5 复数的向量表示

3）三角表示法。利用直角坐标与极坐标的关系

x=rcosθy=rsinθ

得出三角表示：

z=r（cosθ+isinθ） （2-20）

4）指数表示。利用欧拉（Euler）公式

e^iθ=cosθ+isinθ

得出指数表示：

z=re^iθ （2-21）

以上四种复数的表示法可以相互转换，以适应讨论不同问题时的需要。

16.复振幅

由e±iα=cosα±isinα

可得cosα=Re{e±iα} （2-22）

即一实函数可表示为一复函数的实部。将此方法应用于实波函数，则

E（r，t）=E₀（r）cos（k·r-ωt+φ₀）

有 E（r，t）=Re{E₀（r）exp[±i（k·r-ωt+φ₀）]}

通常习惯将指数中ωt项的符号取为负号。按这种规定，则

E（r，t）=Re{E₀（r）exp[i（k·r+φ₀）]e^-iωt} （2-23）

式（2-23）中括号{}内的函数称为复波函数，常用E（r，t）表示。单色简谐波的波场的各场点复波函数中的时间因子e^-iωt都是相同的，故可以将它分离出来，将剩余的空间依赖项记为

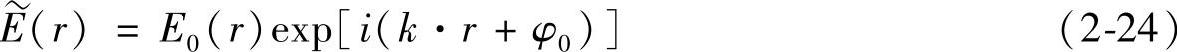
E（r）称为波的复振幅，它的模即实数振幅E₀（r），它的幅角是exp[i（k·r+φ₀）]的指数k·r+φ₀。空间依赖项e^ik·r常称为空间相因子（简称相因子）。

引入复函数的理由如下：

1）从遵循电磁波的传播角度来说，实数描述和复数描述完全是等价的。

2）复振幅的运算一般比实波运算简便得多，从复振幅可以很方便地（乘以e^-iωt再取实部）得到相应的实波函数。

17.场的概念 如果在全部或部分空间里的每一点，都对应着某个物理量的一个确定的值，就说在这空间里确实了该物理量的场。如果这物理量是数量，就称这个场为数量场，如温度场、密度场、电位场等为数量场；若是矢量，就称这个场为矢量场，如力场、速度场为矢量场。

场论中的梯度、散度、旋度可用算子表示：

梯度 gradu=u （2-25）

散度 divA=·A （2-26）

旋度 rotA=×A （2-27）

18.哈米尔顿算子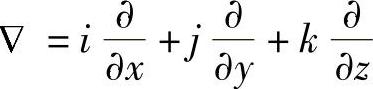 叫做哈米尔顿算子。记号是一个微分运算符号，但同时又要当作矢量看待。

其运算规则如下：

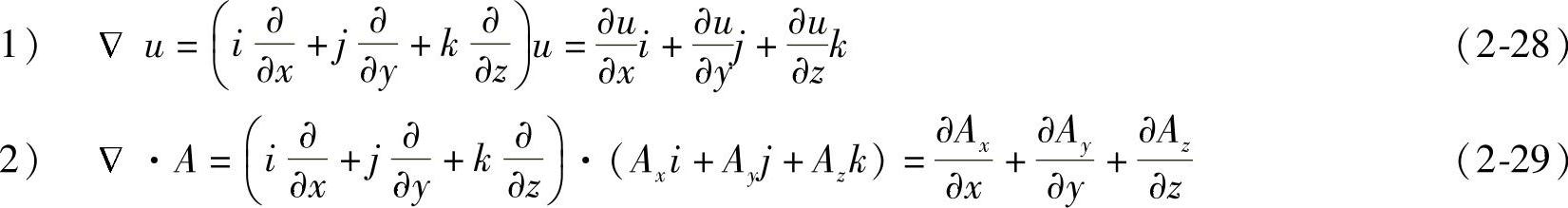
说明：

①算子在计算中具有矢性和微分的双重性质。

②算子的运算规则表明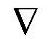，作用在一个数性函数或矢性函数上时，其方式仅有如下的三种：

u·A×A

即在“”之后必为数性函数，在“·”与“×”之后必为矢性函数。

③u为数量场；A为矢量场。

19.麦克斯韦方程组 麦克斯韦方程组可以说明光的波动性，肯定了电磁波的存在，而且具体给出了波的传播速度。

式中 E———电磁波中的电场强度矢量；

H———电磁波中的磁场强度矢量；

μ———介质的磁导率；

ε———介质的电容率，又称介电常数。

式（2-32）、式（2-33）称为E和H的波动微分方程。

20.光速、磁导率、电容率的关系

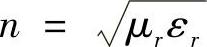
对光学波段，近似有_μr=1，故可认为

式中 c———光速；

μ₀———真空中磁导率；

ε₀———真空中电容率；

μ_r———介质的相对磁导率；

ε_r———介质的相对电容率；

μ———介质的磁导率；

ε———介质的电容率；

v———介质中光速；

n———介质的折射率。

21.倒易点阵 将空间点阵（真点阵或实点阵）经过倒易变换，就得到倒易点阵。倒易点阵的外形也很象点阵，但其上的节点是对应着真点阵的一组晶面。倒易点阵的空间称为倒易空间。

22.对角化 对角化是针对线性代数中的矩阵而言。若矩阵A相似于对角矩阵，则称A可对角化。对角化分为三步：求出A所有的特征值；求出基础解系；列出对角阵P^-1AP。

23.准粒子 准粒子的概念首先来自场论。如果假定，一个体系中存在着大量的“粒子”，这些粒子就好像是一系列自由的粒子组合在一起，并且假定已经知道了这些粒子的所有性质。接下来是怎么知道它们的性质的？在固体物理中，任何一个材料都是由无数的粒子组成的，要研究单个粒子的性质，只能通过某种激发。有激发，当然就有激发谱，所看到的正是这样一个个激发谱。激发谱当然有一条条的谱线，这每一条谱线就对应一种粒子，这个就叫做“准粒子”。所以很多时候，准粒子也可以称为元激发。从凝聚态物理学上，准粒子类似于在相互作用粒子系统中的一个实体，当实体中的一个粒子在系统中穿行并朝着一定方向运动，环绕该粒子的其他粒子云，因为其间的相互作用而脱离原有的运动轨迹，或者“被拖拽着向某个方向运动”。从宏观上看来，这一系统就像一个自由运动着的整体，也就是一个“准粒子”。在凝聚态物理中，引入这样一个“准粒子”的概念非常重要，它是已知的能简化多体问题的方法之一。

24.费米子和玻色子 费米子得名于意大利物理学家费米。玻色子得名于印度物理学家玻色。在量子世界里，所有的成员都有标定各自基本特性的四种量子属性：质量、能量、磁矩和自旋。这四种属性当中，自旋的属性是最重要的。它把不同种粒子王国分成截然不同的两类，根据自旋倍数的不同，科学家把基本粒子分为玻色子和费米子两大类。费米子是像电子一样的粒子，有半整数自旋（如1/2，3/2，5/2等）；而玻色子是像光子一样的粒子，有整数自旋（如0，1，2等）。这种自旋差异使费米子和玻色子有完全不同的特性。没有任何两个费米子能有同样的量子态：它们没有相同的特性，也不能在同一时间处于同一地点；而玻色子却能够具有相同的特性。

自旋是粒子的一种与其角动量（粗略地讲，就是半径与转动速度的乘积）相联系的固有性质。量子力学所揭示的一个重要之点是自旋是量子化的，这就是说，它只能取普朗克常数的整数倍（玻色子，如光子、介子等），或半整数倍（费米子，如电子、质子等）。这些基本粒子在宇宙中的用途可以这样表述：构成实物的粒子费米子（如轻子中的电子、组成质子和中子的夸克、中微子）和传递作用力的粒子玻色子（光子、介子、胶子、W和Z玻色子）。

费米子和玻色子遵循完全不同的统计规律。

（1）费米子。自旋为半整数（1/2，3/2…）的粒子统称为费米子。它服从费米-狄拉克统计。费米子满足泡利不相容原理，即不能两个以上的费米子出现在相同的量子态中。轻子，核子和超子的自旋都是1/2，因而都是费米子。自旋为3/2，5/2，7/2等的共振粒子也是费米子。遵循的费米-狄拉克统计，其中一个显著特点，就是1925年瑞士科学家泡利发现的“泡利不相容原理”，即在一个费米子系统中，绝不可能存在两个或两个以上在电荷、动量和自旋朝向等方面完全相同的费米子。这就像电影院里的座位，每座只能容纳一个人。而玻色子则完全不同，一个量子态可以容纳无穷多个玻色子。因此，也只有玻色子才可能出现玻色-爱因斯坦凝聚现象。例如，锂的两种同位素锂6和锂7分别为费米子和玻色子。图片分别显示在810、510和240nk时，锂6和锂7原子气和原子云照片。可以看到，锂7（左），随着温度的降低所占的尺寸变小，也就是发生了凝聚，而锂6（右）的尺寸则保持稳定，不发生凝聚。这是因为泡利不相容原理的限制，使两个费米子不可能在同一时间占据同一个空间。正因如此，白矮星最终只能在引力作用下坍塌到一个极限尺寸而不再进一步缩小。

（2）玻色子。自旋为整数的粒子称为玻色子。它不遵守泡利不相容原理，在一组由全同粒子组成的体系中，如果在体系的一个量子态（即由一套量子数所确定的微观状态）上，可以容纳的粒子数不限。玻色子所遵循的统计法称为玻色统计法，在低温时可以发生玻色-爱因斯坦凝聚，符合玻色-爱因斯坦统计。玻色子包括：胶子-强相互作用的媒介粒子，自旋为1有8种；光子-电磁相互作用的媒介粒子，自旋为1只有1种。粒子的自旋不像地球自转那样是连续的，而是一跳一跳地旋转着的。

25.声子 声子（Phonon）是晶体中晶体结构集体激发的准粒子，化学势为零，服从玻色-爱因斯坦统计，是一种玻色子。声子本身并不具有物理动量，但是携带有准动量，并具有能量（其中为月华普朗克常数）。根据南部-戈德斯通定理，任何连续性整体对称性的自发破缺，必然对应一个零质量的玻色子。声子就是平移对称性被晶格的点阵结构自发破缺以后对应的玻色子。声子与电子的相互作用，是BCS理论（超导的微观理论）的关键机制。

26.光子 它是一个呈电中性的原子，其正电的质子和负电的电子的数量是相等的。现在由于少了一个负电的电子，所以那里就会呈现出一个正电性的空位———空穴。当有外面一个电子进来掉进了空穴，就会发出电磁波———光子。空穴不是正电子。电子与正电子相遇湮灭时，所发出来的光子是非常高能的。那是两粒子的质量所完全转化出来的电磁波（通常会转出一对光子）。而电子掉入空穴所发出来的光子，其能量通常只有几个电子伏特。

27.激子 导带电子和价带的空穴分别带负、正电荷，彼此间有库仑吸引作用，因此一个空穴和一个电子有可能相互束缚形成一个电中性的复合体，称为激子。

激子（exciton）描述了一对电子与电洞由静电库仑作用相互吸引而构成的束缚态。它可被看作是存在于绝缘体，半导体和某些液体中呈电中性的准粒子。激子是凝聚态物理中转移能量而不转移电荷的基本单位。半导体吸收一个光子之后就会形成一个激子。这个过程实际上是一个电子从价带激发到导带，留下一个处于固定位置带正电的空穴。此时，导带中的电子会受到空穴库仑力的吸引。吸引作用提供了能量平衡，使得激子体系的总能量略小于未束缚的电子和空穴的能量。束缚态的波函数是类氢的，属于奇异原子态；但这个束缚态的束缚能要比氢原子小许多，而激子的半径则比氢原子的要大。这是因为，一方面半导体中存在相邻电子的库仑屏蔽；另一方面电子和空穴构成激子的有效质量较小。电子和空穴的自旋可以是平行或反平行的。自旋通过交换作用发生耦合，于是产生了激子的精细结构。在周期性晶格中，激子的性质与其动量相关。

激子的概念最早由Yakov Frenkel于1931年提出，用于解释绝缘体中的原子激发。他指出激发态可以像实体粒子一样在晶格中穿行而不发生电荷转移。