柔性立管截面优化设计建议

截面设计分两步：

①根据经验初估柔性立管各层尺寸。

②根据柔性立管各层可能的失效，对柔性立管进行局部分析，确定第一步初估的尺寸是否满足表5-2中API 17J规定的柔性立管各层设计准则。如果不满足，则重新估算尺寸，直至满足要求。如果通过调整尺寸仍无法满足，则需要返回材料选择或型式选取阶段，重新选择材料或型式。

对于骨架层厚度的估算应当考虑可能的磨损和腐蚀。

在该阶段选取的截面参数，需要在后面的详细设计阶段进行验证。

表5-2　柔性立管设计准则

1）骨架层尺寸设计

骨架层的主要作用是支撑内压密封层，抵抗外部压力，所以在进行骨架层设计时，主要依据骨架层抗外压的能力。柔性立管的外压主要是由水深产生的压力，骨架层通常设计为互锁的S形。

对于S形骨架层缠绕角度接近90°，其截面形状由平直部分和弯曲部分组成，如图5-16所示。

图5-16　骨架层截面示意图

由于骨架层截面的复杂性，因此用理论方法来分析是不可行的。但是由于骨架层截面以接近90°的角度互锁而成，在立管纵向方向形成一个类似圆管的几何形状，因此单位长度的该圆管可被当作一个圆环。圆环所能承受的最大外压为

式中　R——等效半径；

t equivalent——等效厚度；

E——材料的弹性模量。

式（5-1）中EI为单位长度圆管的弯曲刚度，因此如果已知骨架层单位长度的等效弯曲刚度，就能获得其所能承受的最大外压。

骨架层截面在外压下的失效取决于制作过程中产生的初始缺陷，最重要的缺陷为初始椭圆度。有缺陷的截面所能承受的最大外压比式（5-1）中所得数值更小，可根据铁摩辛柯提及的公式进行修正。

在骨架层设计过程中，首先将S形截面互锁骨架层圆管等效为实壁圆管，根据铁摩辛柯壳屈理论对实壁圆管施加水压和渗透气体等压力进行应力校核，判断骨架层应力是否满足要求。

2）内压密封层尺寸设计

内压密封层的作用是形成一个密封的空间，保证内部介质的输送。

由骨架层外径确定内压密封层的内径，根据内压密封层的加工工艺和蠕变量确定内管层厚度和外径。防止裂缝扩展影响到整个输送的要求，内压密封层可以根据需要设计成单层或多层。

3）抗压铠装层尺寸设计

抗压铠装层的主要作用是抵抗内部的输送压力，其截面形式可以是Z形、C形、T形等，主要是由厂家的抗压铠装层设备决定的。

4）抗磨层尺寸设计

由抗压铠装层、抗拉铠装层、保温层外径确定抗磨层内径，根据抗磨层加工工艺和经验确定抗磨层厚度和外径。抗磨层尺寸确定主要依据经验值及设备的制造能力。

5）抗拉铠装层尺寸设计

抗拉铠装层主要作用是承受轴向拉力，轴向拉力主要是由内压和外部水压等产生。在初步设计时，通过内压值计算得出轴向拉力，利用轴向拉力初步估算抗拉铠装层尺寸；同时考虑抗拉铠装层设备的制造能力、扁钢的覆盖率等因率，确定扁钢的尺寸。

6）中间包覆层尺寸设计

由抗拉铠装层、抗磨层尺寸确定中间包覆层内径，根据中间包覆层加工工艺和经验确定中间包覆层的厚度和外径。

7）保温层尺寸设计

由中间包覆层外径确定保温层内径，根据柔性立管总传热系数确定保温层的厚度和外径。

8）外包覆层尺寸设计

由保温层和抗磨层尺寸确定外包覆层内径，根据外包覆层加工工艺和经验确定外包覆层的厚度和外径。外包覆层可以是单层或双层结构。采用双层结构主要考虑到最外层包覆受外力破坏时，裂缝扩展不会影响到里面一层的外包覆，不会影响柔性立管的使用。

根据柔性立管整体结构功能和设计准则，对柔性立管进行截面设计分析，得到柔性立管的刚度（弯曲刚度、轴向刚度、扭转刚度）、总传热系数、弯曲半径（最小弯曲半径、存储弯曲半径和操作弯曲半径）和极限轴向拉力等截面特性。

9）弯曲刚度

由于骨架层及抗压铠装层的绕角接近90°且为柔性连接，故对总体弯曲刚度的贡献在初始设计时可不予考虑。拉伸钢丝对初始弯曲刚度有影响，但在一定弯曲曲率时产生滑移，为保守起见，总体弯曲刚度设计时也可暂不考虑。包覆层如果为带状缠绕，通常绕角接近90°，对弯曲刚度影响也不予考虑。

因此弯曲刚度计算只考虑聚合物层：

式中　D i——聚合物层的外径；

d i——聚合物层的内径；

E i——聚合物材料的弹性模量。

10）轴向刚度

骨架层及抗压铠装层的绕角接近90°，对总体轴向刚度的贡献在初始设计时可不予考虑。

轴向刚度计算考虑聚合物层和抗拉铠装层。

聚合物层轴向刚度计算公式如下：

式中　E i——聚合物材料的弹性模量；

A i——聚合物层的截面面积。

抗拉铠装层轴向刚度计算公式如下：

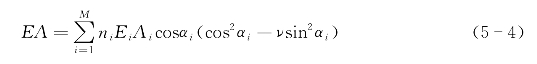
式中　n i——单层抗拉铠装层中的扁钢根数；

E i——抗拉铠装层材料的弹性模量；

A i——抗拉铠装层扁钢的截面面积；(www.xing528.com)

αi——扁钢的缠绕角度；

ν——抗拉铠装层整体的泊松比。

11）扭转刚度

扭转刚度计算考虑聚合物层和抗拉铠装层。

聚合物层扭转刚度计算公式如下：

式中　Gi——聚合物材料的剪切模量；

J i——聚合物层的截面极惯性矩。

抗拉铠装层扭转刚度计算公式如下：

式中　n i——单层抗拉铠装层中的扁钢根数；

E i——抗拉铠装层材料的弹性模量；

A i——抗拉铠装层扁钢的截面面积；

αi——扁钢的缠绕角度；

r i——抗拉铠装层中半径。

12）弯曲半径

柔性立管能够弯曲到的最小半径叫作最小弯曲半径（MBR），如图5-17所示。

图5-17　最小弯曲半径示意图

在计算最小弯曲半径时，各结构的最小弯曲半径应分别计算。对于螺旋缠绕的铠装层，最小弯曲半径主要考虑相邻绕组间间隙关闭的情况，聚合物层主要考虑由于应变达到最大值时的弯曲半径。整管的最小弯曲半径应为各结构层最小弯曲半径的最大值：

式中　R 1min——各聚合物层的最小弯曲半径；

R 2min——骨架层的最小弯曲半径；

R 3min——抗压铠装层的最小弯曲半径；

R 4min——抗拉铠装层的最小弯曲半径。

聚合物层的最小弯曲半径计算如下：

式中　r o——聚合物层外半径；

εmax——聚合物层的允许最大应变。

骨架层互锁结构如图5-18所示。在骨架层弯曲时，受拉侧相邻绕组间的间隙会增大，受压侧相邻绕组间的间隙会减小。当相邻绕组发生接触，就会发生锁死。

图5-18　骨架层互锁结构示意图

抗拉侧间隙最大时弯曲半径为

抗压侧间隙最小时弯曲半径为

式中　R t——抗拉侧间隙最大时的最小弯曲半径；

R c——抗压侧间隙最小时的最小弯曲半径；

r——骨架层中半径；

εt——抗拉侧相邻绕组的最大相对运动量；

εc——抗压侧相邻绕组的最大相对运动量。

抗压铠装层互锁结构与骨架层类似，如图5-19所示。在弯曲时，受拉侧相邻绕组间的间隙会增大，受压侧相邻绕组间的间隙会减小。当相邻绕组发生接触，就会发生锁死。

图5-19　抗压铠装层互锁结构示意图

抗压铠装层最小弯曲半径的计算方法与骨架层相同。

抗拉铠装层弯曲到一定曲率时，相邻绕组间的间隙将逐渐变小。当抗压侧的间隙为零时，抗拉铠装层将锁死。其最小弯曲半径计算公式为

式中　r m——抗拉铠装层中半径；

εc——抗压侧相邻绕组的最大相对运动量；

r——抗拉铠装层中半径；

t——抗拉铠装层的扁钢厚度；

R f——抗拉铠装层的覆盖率。

整管的最小弯曲半径应为各结构层最小弯曲半径的最大值，存储弯曲半径为最小弯曲半径的1.1倍，操作弯曲半径为存储弯曲半径的1.5倍。