影响函数法的作用及应用

影响函数法是一种离散化的方法。它的基本思想是：首先将轧辊离散成若干单元；然后按照相同的单元离散轧辊所承受的载荷及轧辊弹性变形，先确定当单位力作用于各单元时辊身各点处引起的变形，再施加全部载荷，将全部载荷在各单元引起的变形叠加，即可求出各单元的变形值，从而可以确定出口处的厚度分布和张力分布［144－146］。

对各单元序号的编排共有两种方法，如图4－12所示。第一种方法是沿辊身全长自右向左排列，共N个单元，这种方法用于分析整个辊系各辊之间的力和变形关系；第二种方法是沿左右两半辊身分别由中心向两端排列N2＝N/2，这种方法适用于悬臂梁的变形及单位宽轧制力、断面厚度等对称量的研究。

图4-12　单元划分及序号编排

根据影响函数的概念可以得到如下基本方程。

4.3.1.1　力变形关系方程

1.工作辊弹性弯曲方程

将工作辊分解为两个悬臂梁，分别求出左、右两部分的挠度：

式中：YwL、YwR分别为工作辊辊身左、右部分的挠度；Gw为工作辊弯曲影响函数矩阵，；QwiL、QwiR分别为工作辊与中间辊间左、右部分的接触压力；PL、PR分别为工作辊辊身左、右部分的轧制压力；G为工作辊弯辊力影响函数向量，G＝[g（1）…　g（N）]T；

wfwfwfwf2Fw为工作辊弯辊力。

2.中间辊弹性弯曲方程

将中间辊分解为两个悬臂梁，分别求出左、右两部分的挠度：

式中：YiL、YiR分别为中间辊辊身左、右部分的挠度；Gi为中间辊弯曲影响函数矩阵，QibL、QibR分别为中间辊与支撑辊间左、右部分的接触压力；Gif为中间辊弯辊力影响函数向量，Gif＝[gif（1）…　gif（N2）]T；Fi为中间辊弯辊力。

3.支撑辊弹性弯曲方程

将支撑辊分解为两个悬臂梁，分别求出左、右两部分的挠度：

式中：YbL、YbR分别为支撑辊辊身左、右部分的挠度；Gb为支撑辊弯曲影响函数矩阵，

4.轧制压力引起的工作辊弹性压扁方程

沿轧件与轧辊接触区的全长求出轧制压力引起的工作辊弹性压扁量，即

式中：Yws为轧制压力引起的工作辊弹性压扁向量；Gws为轧制压力引起的工作辊弹性压扁影响函数矩阵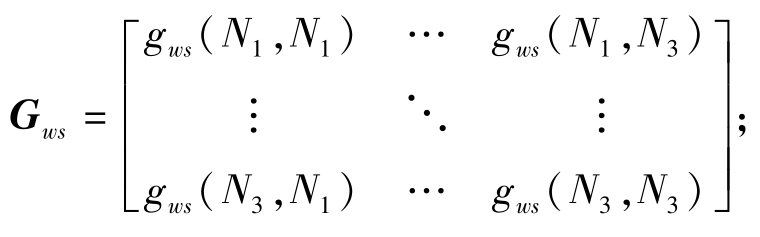，F为轧制压力向量。

5.工作辊和中间辊之间的弹性压扁方程

沿工作辊和中间辊接触区的全长求出弹性压扁量，即

式中：Ywi为工作辊和中间辊辊间压力引起的弹性压扁向量；Gwi为工作辊和中间辊辊间压力引起的弹性压扁影响函数矩阵，Qwi为工作辊和中间辊辊间压力向量。(www.xing528.com)

6.中间辊和支撑辊之间的弹性压扁方程

沿中间辊和支撑辊接触区的全长求出弹性压扁量，即式中：Yib为中间辊和支撑辊辊间压力引起的弹性压扁向量；Gib为中间辊和支撑辊辊间压力引起的弹性压扁影响函数矩阵，Qib为中间辊和支撑辊辊间压力向量。

4.3.1.2　平衡方程

1.工作辊平衡方程

用工作辊在垂直方向上的受力平衡，可以建立工作辊平衡方程：

式中：p（n）为第n测量段的轧制力；qwi（u）为u单元的工作辊与中间辊之间的辊间压力；N1为工作辊与中间辊非接触长度一半的测量段个数（等于中间辊与支撑辊非接触长度一半的测量段个数）；N3为工作辊与中间辊接触长度的测量段个数（等于中间辊与支撑辊接触长度的测量段个数）；n、u为测量段号。

2.中间辊平衡方程

用中间辊在垂直方向上的受力平衡，可以建立中间辊平衡方程：

式中：qib（v）为v单元的中间辊与支撑辊之间的辊间压力，v为测量段号。

4.3.1.3　变形协调关系方程

1.轧件和工作辊之间的变形协调方程

轧件和工作辊之间的变形协调方程为

式中：H为轧件轧后在过中心点的水平线以上的高度，H＝［h（N1）…　h（N3）］T；H0为中心点处轧件轧后高度的 1/2，H0＝；Yws0为中心点处轧制压力引起的工作辊弹性压扁量，；Yw为工作辊辊身全长的挠度；Mw为工作辊凸度，Mw＝［mw（N1）…　mw（N3）］。

2.工作辊和中间辊之间的变形协调方程

工作辊和中间辊之间的变形协调方程为

式中：Ywi0为中心点处工作辊和中间辊之间的辊间压力引起的弹性压扁量，Ywi0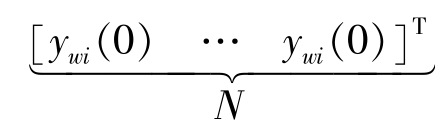＝；Yi为中间辊辊身全长的挠度；为工作辊凸度，＝［mw（1）…　mw（N）］；Mi为中间辊凸度，Mi＝［mi（1）…　mi（N）］。

3.中间辊和支撑辊之间的变形协调方程

中间辊和支撑辊之间的变形协调方程为

式中：Yib0为中心点处中间辊和支撑辊之间的辊间压力引起的弹性压扁量，Yib0＝；Mb为支撑辊凸度，Mb＝[mb（1）…　mb（N）]。