基于Bandelet变换的IVUS和IV-OCT图像融合技术

（1）Bandelet变换简介

小波变换是一种“稀疏”的表示方式，即将信号的大部分能量集中在少量表示系数中。但是由一维小波生成的二维离散小波变换仅具有有限的方向，不考虑图像的几何结构，仅适用于处理一维空间中的点奇异性。二维空间甚至高维空间不仅存在点奇异性，还存在线或面奇异性，而小波变换不能取得类似分析一维信号时的最优逼近。为了处理高维信号的奇异性，人们提出了多尺度几何分析，它是一种带有方向性的表示方式，是以小波变换为基础的方法，具有局部性、方向性和多尺度性，对于高维空间的信号分析可以达到最优逼近。目前，多尺度几何分析方法主要包括Ridgelet变换、Curvelet变换、Contourlet变换和Bandelet变换等。

其中Bandelet变换是一种基于边缘的图像表示方法，可充分利用图像的边缘信息，能自适应地跟踪图像的几何正则方向。第一代Bandelet对图像进行空域分割，Bandelet基函数在单个Bandelet带内正交，但不是全局正交的，而且第一代Bandelet基函数不能提供对几何流的多尺度分解，且运算量大，占用内存。之后，文献［41］提出了第二代Bandelet变换，其主要思想是结合小波变换与Bandelet化得到几何流和Bandelet系数，经过融合规则进行逆变换重构图像。Bandelet化的实施对象是小波变换的各高频子带，可以分为两步进行：第一，沿几何流对小波系数进行重采样，得到一维信号；第二，对一维信号进行一维小波变换，得到Bandelet系数^［42］。

选定高频子带内的一个正方形区域，区域内的系数具有很强的关联性，为了使系数离散化进而消除关联性，可以将区域内的小波系数重排为一维形式。因此，确定重排的方式至关重要。小波的重排必须是可逆的，以此保证可以从重排的一维信号中恢复二维信号。设几何流方向为d且相对于水平的倾角为θ，几何流垂直方向记为 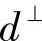，小波系数的位置坐标为（k₁，k₂），将其垂直投影到 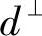上，在 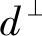上的位置表示为 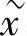，则从二维坐标（k₁，k₂）到一维坐标x～的投影公式如下^［42］：

这样，区域内的每个坐标对应一个一维坐标 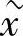，不同的二维坐标可能对应相同的一维坐标。对区域内的每个点，按坐标 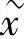的大小排序，设序号为i，令

得到一维信号f_d。

上述过程是将小波系数的排布式从二维转换到一维，目的就是为了得到一维平滑信号f_d，对一维信号f_d作一维小波变换，大幅值系数个数相对减少，能量进一步向少数系数集中，从而得到更好的融合效果。

Bandelet化的过程是可逆的，根据几何流方向对小波系数进行反排序，之后一维小波变换的逆变换即可恢复原来的二维小波系数。一般情况下，图像的几何流是未知的，只有在局部区域才可以用直线逼近几何流，而且不同区域内几何流方向不同。Bandelet化依赖于几何流，因此在实施Bandelet化之前，必须对各高频子带进行分割，并且确定各分割区域内的几何流。

（2）基于第二代Bandelet变换的IVUS和IV-OCT图像融合算法

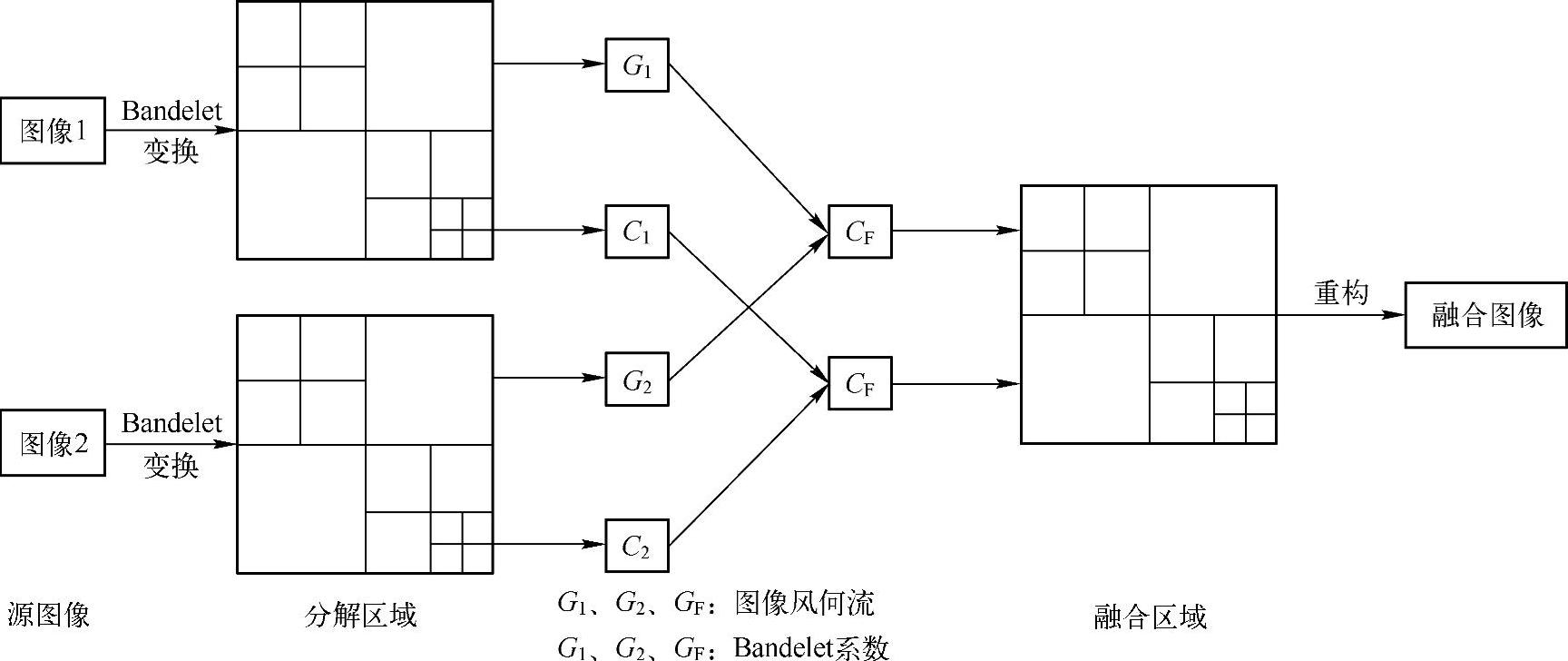
基于Bandelet变换的融合算法流程如图4-49所示，对于完成了配准的IVUS和IV-OCT图像进行基于Bandelet变换的图像融合算法的具体步骤如下：

(www.xing528.com)

图4-49 基于Bandelet变换的融合算法流程

1）对两幅源图像作二维离散小波变换，得到高频子带和低频子带图像。

2）对各高频子带图像分别进行四叉树分割，得到尺寸为N×N的Bandelet块，同时得到各分割区域内的几何流G_F（i）（i表示第i个分割区域），将圆周角［0，π）离散为N²-1个值，则几何流的倾角θ为

式中，k＝0，1，...，N²-2；j是待融合图像的总数，此处j＝2。

3）对各Bandelet块实施Bandelet化，得到Bandelet系数。对于二维小波变换后的低频小波系数虽然未Bandelet化，也称其为Bandelet系数。

4）采用融合规则得到几何流G_F（i）和Bandelet系数C_F（x，y，i），并进行逆Bandelet变换重构融合图像。采用融合规则对几何流和Bandelet系数进行融合。对于几何流，采用的最大值融合规则如下：

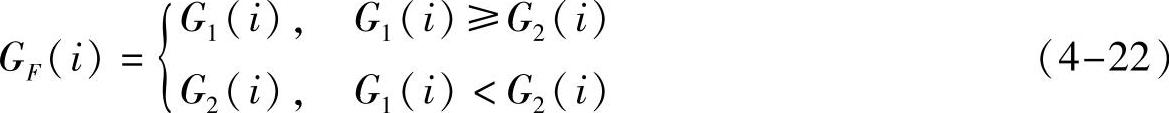
其中G_F（i）是融合图像第i个区域的的几何流。对于Bandelet系数，采用的最大绝对值融合规则如下：

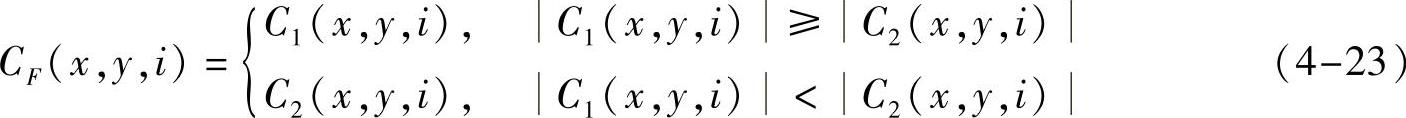
其中C_F（x，y，i）是融合图像在点（x，y）的Bandelet系数。几何流反映图像的梯度信息，Bandelet系数反映图像整体轮廓和细节信息，二者的融合规则是根据IVUS及IV-OCT图像的灰度信息确定的。