基于特征点的IVUS与IV-OCT图像配准优化方法

本节介绍一种对同一段血管的、在相同管腔位置采集的、包含钙化斑块或者血管分叉的IVUS和IV-OCT横断面图像进行配准的方法。流程图如图4-42所示，方法的基本思路是以IV-OCT图像作为参考图像，IVUS作为待配准图像，选择钙化特征点或者血管分叉点作为配准依据，根据空间变换模型确定两幅图像之间的变换参数，进而对IVUS图像进行相应的变换。主要包括如下步骤：图像预处理、特征提取、确定空间变换模型、图像插值及变换等。

（1）图像预处理

因成像设备不同，IVUS和IV-OCT图像的尺寸不同，可能导致提取图像特征时存在差异，因此在进行后续处理之前，需将两种图像的尺寸统一。IV-OCT图像为RGB格式的彩色图像，但是其中并不包含可用于区分不同血管壁组织和斑块组织的颜色信息。因此为了减小后续处理的数据量，提高算法效率，需首先对IV-OCT图像进行灰度化处理。

（2）提取特征点

根据粥样硬化斑块的组织成分及其在IVUS和IV-OCT图像中的不同特征表现，可将其分为四类：脂质性斑块、纤维性斑块、钙化性斑块及混合性斑块。其中钙化斑块在两种成像模式中均具有区别于其他三类斑块的明显的特征：IVUS图像中的钙化斑块表现为强回声区，且其后伴有负性声影；IV-OCT图像中的钙化斑块表现为边界清晰且均匀的低信号区，并伴有较弱的信号衰减，如图4-43所示。

与其他血管结构相比，血管分叉具有特殊的形态特征：IVUS图像中的血管分叉表现为血管腔有一定的偏心率，分叉处具有明显的强回声区；IV-OCT图像中的血管分叉表现为具有偏心率的低回声区，如图4-44所示。

按照方法的自动化程度，可将从灰度图像中提取特征点的方法分为手动标记和自动检测两种方式。后者包括Harris算子^［39］和尺度不变特征变换（Scale Invariant Feature Transform，SIFT）算子^［40］等。

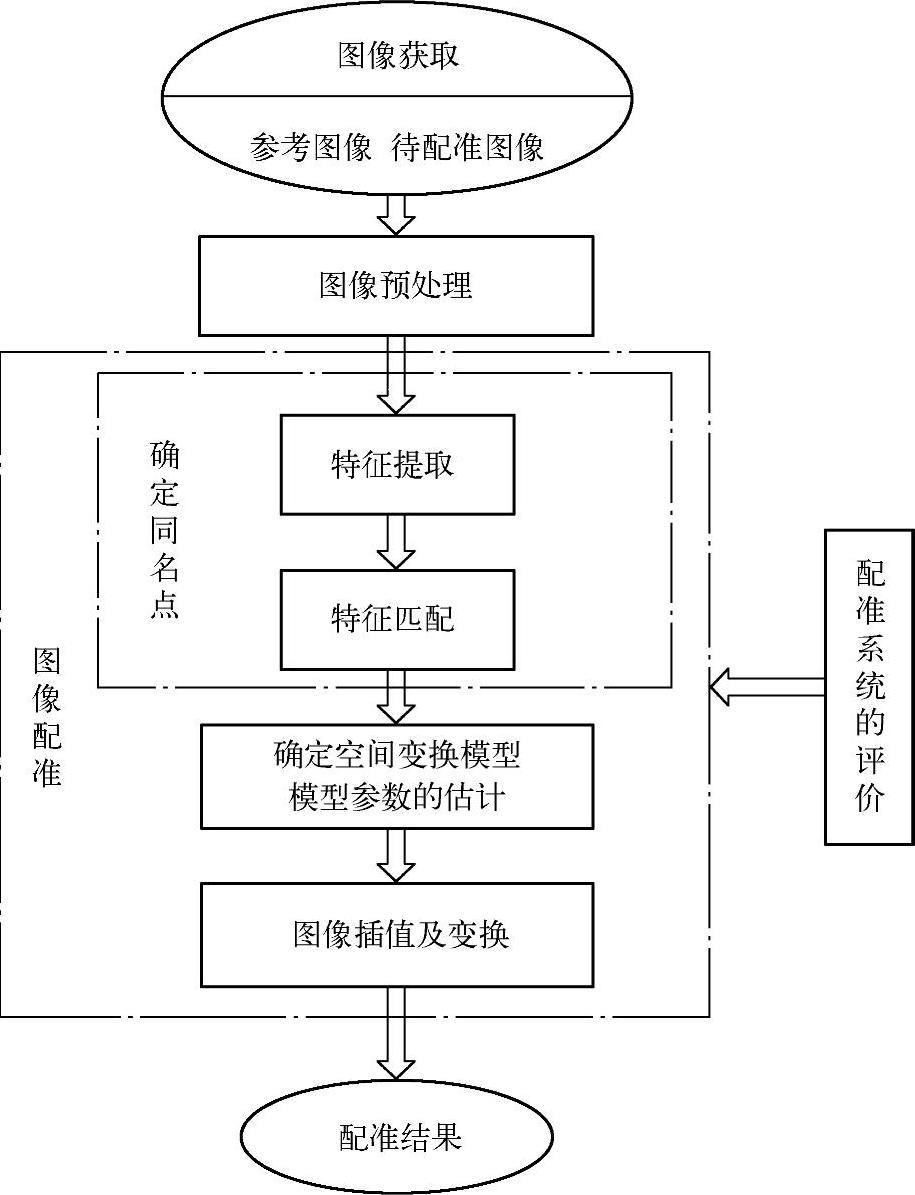
图4-42 基于特征点的IVUS和IV-OCT图像配准流程图

（3）图像空间的几何变换

图像空间的几何变换就是将原图像的某点映射到目标图像的新坐标中，但不改变像素值，分为线性变换和非线性变换两种，常用的图像空间变换模型如图4-45所示。线性变换主要包括刚体变换、相似变换、仿射变换和投影变换，如图4-46所示。刚体变换是最简单的空间变换模型，数学表达式为

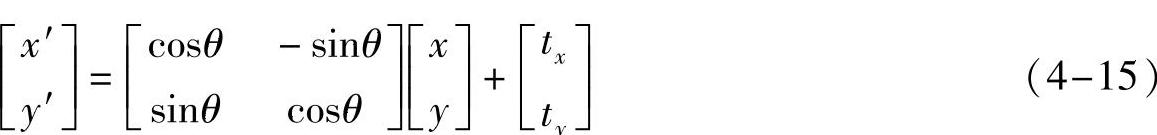
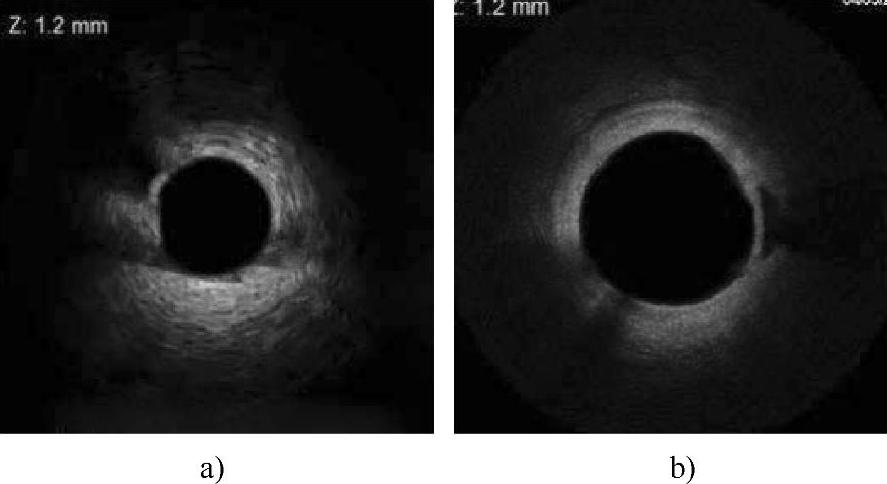
图4-43 包含钙化斑块的一帧IVUS和IV-OCT图像

a）IVUS管腔横截面图像 b）IV-OCT管腔横截面图像

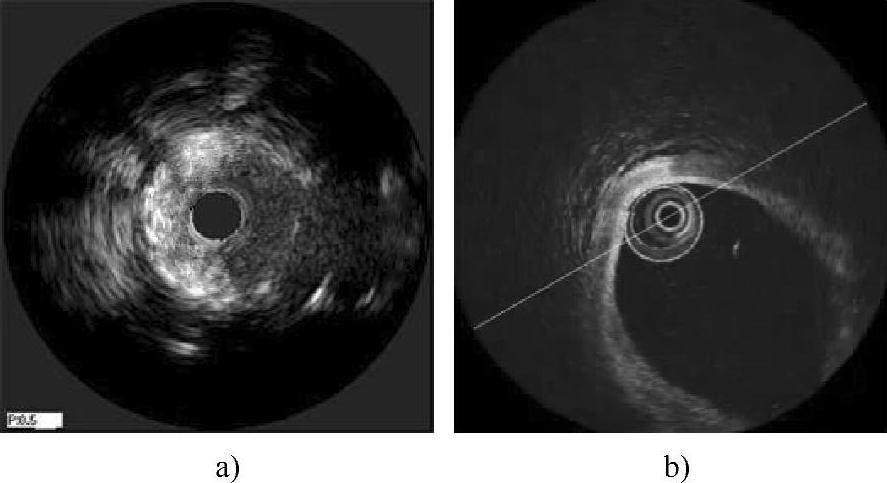
图4-44 包含血管分叉的一帧IVUS和IV-OCT图像

a）IVUS管腔横截面图像 b）IV-OCT管腔横截面图像

式中，（x，y）为原始图像中某点的坐标；（x′，y′）为其变换后的坐标；θ为旋转角度；t_x和t_y分别为x和y方向平移参数。刚体变换保证变换前后待配准图像中任意两点之间的几何关系保持不变，同时图像的尺寸和目标物体的形状等均不改变。

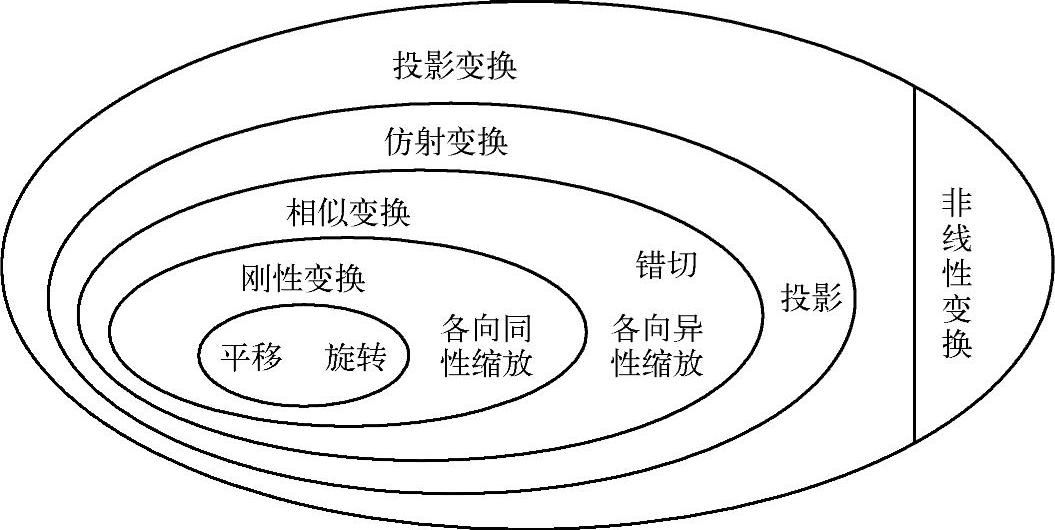
图4-45 常用的图像空间变换模型(www.xing528.com)

相似变换是在刚体变换的基础上引入尺度参数S，改变图像的尺寸，公式如下：

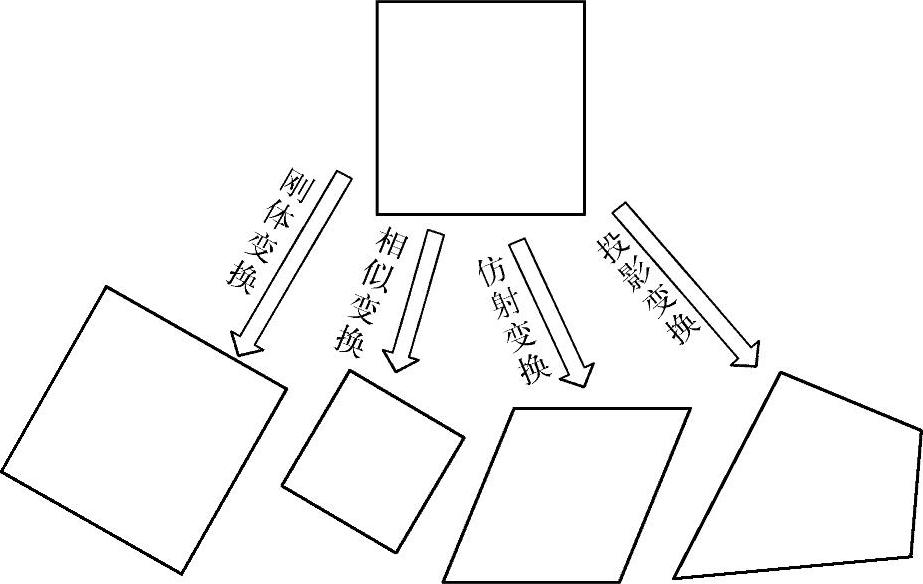
图4-46 图像空间线性变换示例

相似变换包括平移、旋转和缩放。对于由于拍摄时间或角度不同造成图像的平移、旋转或缩放等问题，应用相似变换可以有效解决图像之间的配准问题。

仿射变换是更具一般形式的相似变换，其数学表达式如下：

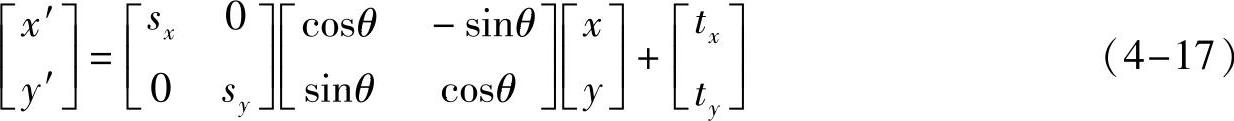
式中，s_x和s_y分别表示不同方向上的尺度参数。仿射变换后，图像的形状及尺寸会发生改变。当s_x＝s_y时，即为相似变换，所以仿射变换是更具一般形式的相似变换。

投影变换较复杂，主要应用于三维图像配准中，它改变了直线间的平行关系。非线性变换又称为弹性变换，一般用代数多项式来表示，它将一条直线映射成曲线，适用于全局性形变或局部形变的图像配准问题。

在不考虑血管腔弹性形变的情况下，假定IVUS和IV-OCT两种成像模式的拍摄条件一致，那么只需考虑IV-OCT和IVUS之间的成像差异，包括由于成像视野和各自探头伸入血管腔的角度不同造成的成像角度不同。也就是说IVUS图像对应的变换类型需要实现相应的平移、缩放及旋转变换，即对应的空间变换模型是相似变换模型。

（4）匹配特征点

利用相似变换模型的最小二乘法闭合公式如下：

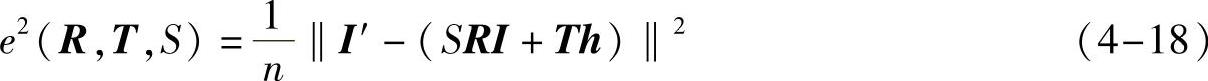
确定待配准的两幅图像特征点对之间的对应关系，即计算参考图像与标准图像的特征点坐标之间的变换参数。式（4-18）中，i＝1，2，..，n；n是控制点的对数；R是2×2的旋转矩阵；T是2×1的平移矩阵；S是尺度参数；e²是均方差；I＝（I₁，I₂，...，I_n）指待配准图像；I_i＝（x_i，y_i）^T为待配准图像中特征点的坐标；I′＝（I′₁，I′₂，...，I′_n）指变换后图像；I′_i＝（x_i′，y_i′）^T为I_i变换后相应的坐标；h＝（1，1，...，1）。当均方差e²（R，T，S）值最小时得到的R、T、S的取值，即为特征点对之间的变换关系。

（5）图像插值

在对待配准的IVUS进行相似变换时，可能会映射到IVUS图像的非整数坐标位置上，此处的灰度值需要通过插值技术来确定。插值技术主要分为最近邻插值法、双线性插值法及双三次插值法。其中最近邻插值法是最简单的方法，即选取距离最近的像素灰度值赋值给待插值点，如图4-47所示，适用于各相邻像素之间灰度值变化较小的情况，但是结果图像的连续性不好；双线性插值法解决了图像灰度值不连续的问题，利用待插值点四个相邻像素的灰度值分别在水平及垂直方向进行线性插值，如图4-48所示，其结果不受水平及垂直方向插值先后顺序的影响，且计算量适中，但会造成图像边缘平滑；双三次插值法不仅受四个直接相邻像素的灰度值影响，同时要考虑该点周围4×4邻域内16个邻点灰度值对待插值点的影响，可以在一定程度上增强图像边缘，但是计算量较大。

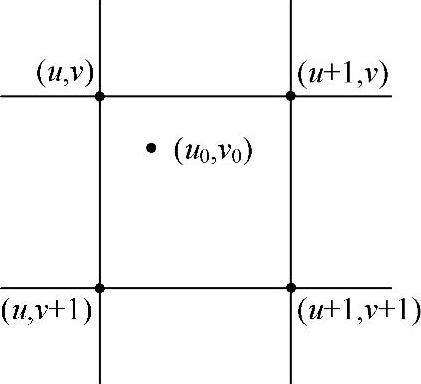
图4-47 最近邻插值示意图

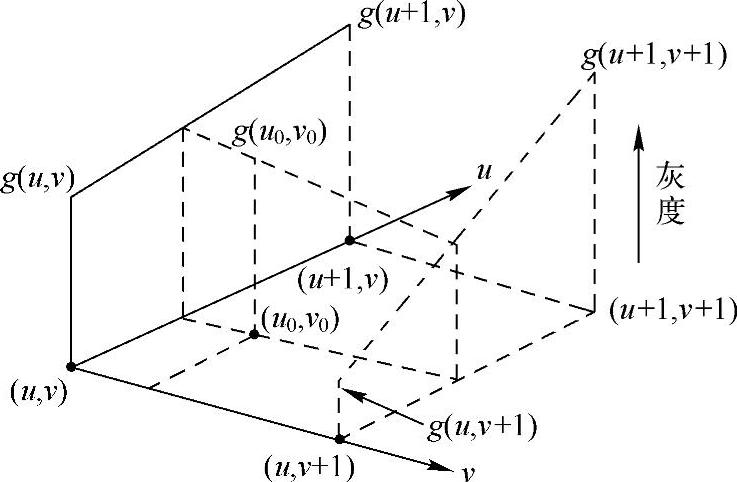
图4-48 双线性插值示意图