图像融合基础理论解析

图像融合是信息融合的重要分支，它将不同传感器采集的同一目标的不同图像或同种传感器以不同成像方式、不同成像时间采集的不同图像，融合成一幅图像，从而使得融合图像能够更全面、清晰、准确地反映多重原始图像的信息，提高图像信息的利用率，更适合视觉感知和计算机处理。多模图像融合具有以下优势：充分利用多模图像的冗余信息，提高融合图像的可靠性；充分利用多模图像的互补信息，改善单一模态图像的不足，增强其某些不明显的特征，使融合图像具备精确、全面、丰富的信息；提高融合系统的鲁棒性，从而减少图像的噪声影响，提高图像质量；扩大融合系统工作范围，例如时间范围、空间范围。

（1）图像融合的三个层次

图像融合主要分为四个步骤实现：图像预处理、图像配准、图像融合及融合评价。按照由低到高的次序可将图像融合归纳为三个层次：像素级融合、特征级融合、决策级融合，如图4-38所示。在实际应用中，要根据具体应用选择合适的融合方式从而获得最佳的融合效果。

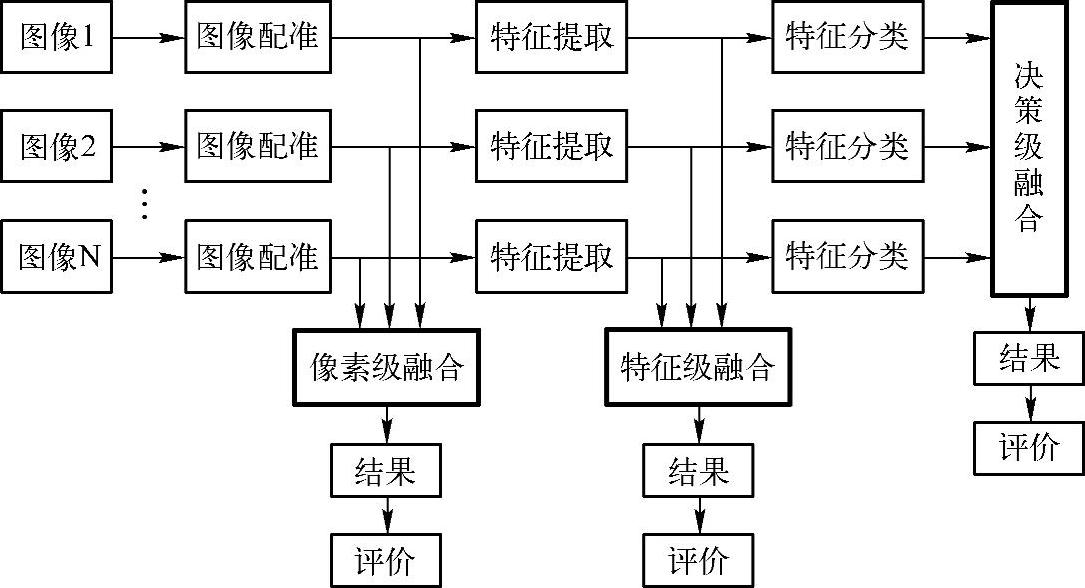
图4-38 图像融合的三个层次

像素级融合属于最低层次的图像融合，是指在几何配准条件下，直接对原始多模图像进行信息综合分析。该层次的图像融合准确性最高，能够提供后两个层次的融合所不具备的细节信息，因此也是应用最广泛的融合方式。但需处理的信息量较大，不适合实时应用。

特征级融合属于中间层次的图像融合，是指对预处理后的图像进行特征提取，综合处理和分析得到的特征信息如边缘、形状、纹理和区域等。通过对信息进行筛选，达到了减少冗余信息同时保留足够数量的重要信息的目的，大大减小了计算量，利于实时处理。其缺点是对原始图像数据应用稀疏表示，易丢失信息，影响融合效果。特征级融合的主要方法有聚类分析方法、Dempster-Shafer推理方法、信息熵方法、表决方法级神经网络方法等。

决策级融合是最高层次的融合，是指对预处理后的每幅图像分别进行特征提取、识别或判决，建立对同一特征的初步决策，然后融合这些决策生成整个融合系统的联合决策。它需要大型数据库和专家决策系统进行分析、推理、识别和判决。优点是实时性最好，具有一定的开放性和容错能力，缺点是信息损失量较大。目前，常用的决策级图像融合方法主要有贝叶斯估计法、模糊聚类法及专家系统等。

（2）像素级融合算法

像素级融合算法主要包括简单融合、金字塔分解融合、基于小波变换的融合和基于多尺度几何变换的融合算法等。其中后三种算法均属于多尺度分析融合算法，流程图如图4-39所示，对图像的融合过程类似于人类视觉系统对图像不同尺度、不同空间分辨率和不同分解层的细节信息处理，可获得更好的融合效果。

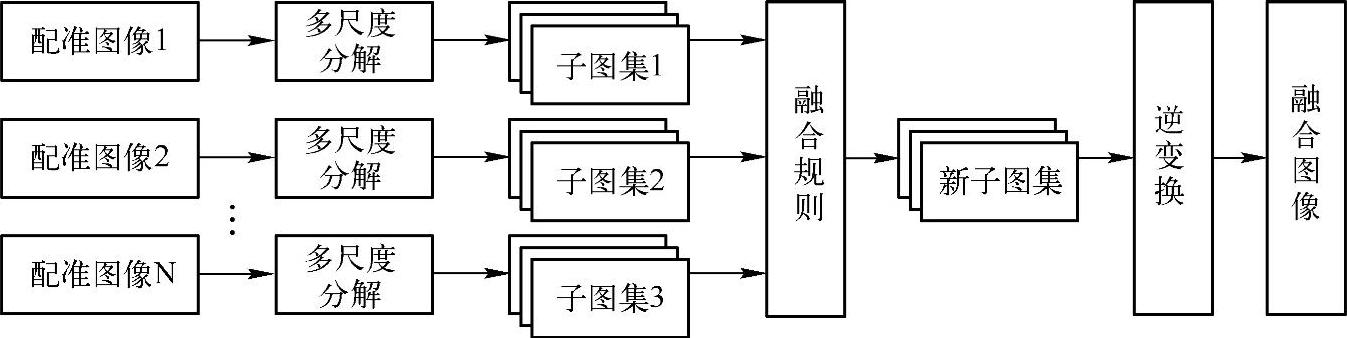
图4-39 多尺度分析融合算法的流程图

简单融合算法主要包括加权平均法、颜色空间变换法、人工智能法等。加权平均法是最简单、最基本的图像融合方法，基本思想是将多模原始图像的对应像素灰度值进行加权处理。颜色空间变换法是将多模图像映射到某个固定的颜色通道上再合并分量成为一幅彩色的融合图像，其中最典型的是基于IHS（Intensity-Hue-Saturation）模型变换的融合。人工智能法不需要确定精确的融合模型，适用于融合难以寻找到合适模型的多模图像，例如人工神经网络、脉冲耦合神经网络、模糊理论、粗糙集理论。

金字塔分解融合算法的基本思想是对待融合的多模图像进行金字塔分解，建立待融合图像的金字塔结构，提取各自的特征信息，对各层次分解图像在多尺度、多分辨率、多分解层的条件下按照一定的融合规则融合成结果图像的金字塔图像，再对金字塔图像进行逆变换得到融合图像。金字塔分解融合算法主要包括拉普拉斯金字塔法、对比度金字塔法、梯度金字塔法等。相较于简单融合算法，金字塔分解算法虽然可得到更好的融合效果，但是分解过程中仍然会损失高频信息，同时分解图像之间的相关性会导致重构图像的不稳定。为了解决这一问题，小波变换以其良好的时频域特性、多分辨率特性、方向性等优势成为图像融合领域较理想的工具。

（3）小波变换融合算法

傅里叶变换是信号处理领域应用最广泛的一种分析手段，它将信号分解成一系列不同频率的正弦波叠加，为了解信号的频率成分提供了很好的分析工具。但是傅里叶的一个严重不足是在变换的时候会丢掉时间信息，因此无法根据傅里叶变换的结果判断一个特定信号是在什么时候发生的。之后，Gabor提出了著名的Gabor变换，进一步发展成为短时傅里叶变换（Short Time Fourier Transform，STFT），其基本思想是给信号加一个小窗，然后对小窗内的信号进行傅里叶变换，因此该变换反映了信号的局部特征。STFT的窗函数的大小和形状都与时间和频率无关，这对于分析时变信号来说是不利的。小波变换不但继承和发展了局部化思想，而且克服了窗口大小不随频率变化的特点，它利用小波基取代传统的三角函数，进而对函数进行分解与综合，能通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析，是对非平稳函数进行分析的更方便的工具。

由一维离散小波变换的Mallat算法可以得到对二维图像的小波分解算法，公式如下：

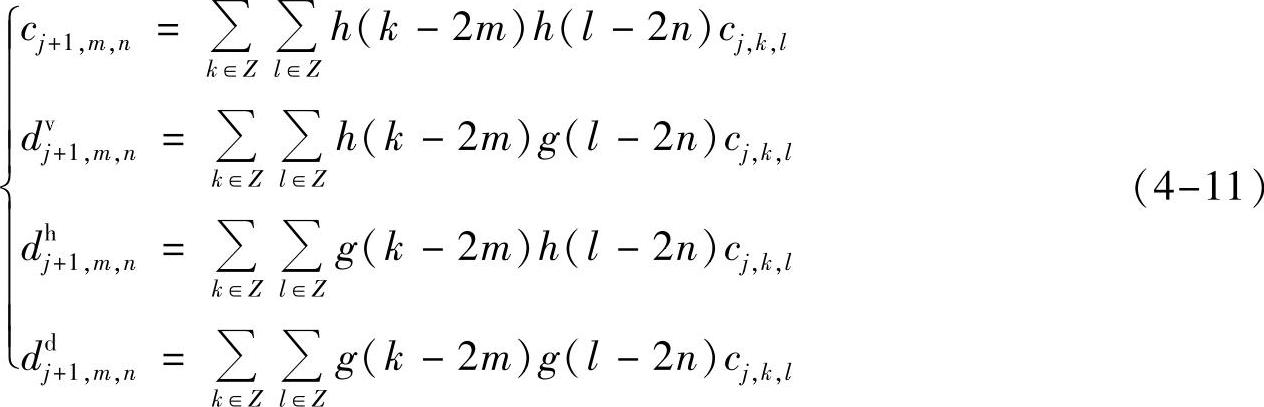
以及重构算法，公式如下：(www.xing528.com)

式中，C_j＋1和C_j分别表示第j＋1和第j层分解图像的低频小波系数；d^v_j＋1、d^h_j＋1和d^d_j＋1分别表示第j＋1层分解图像垂直、水平及对角方向的高频小波系数；h（k-2m）和h（l-2n）分别表示沿y和x方向对图像进行低通滤波并采样；g（k-2m）和g（l-2n）分别表示沿y和x方向对图像进行高通滤波并采样；h（m-2k）和h（n-2l）分别表示沿y和x方向对图像插值并低通波；g（m-2k）和g（n-2l）分别表示沿y和x方向对图像插值并高通滤波。

用H_r和H_c分别表示对阵列 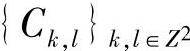的行和列作用的镜像共轭滤波器的系数矩阵，G_r和G_c分别是对阵列 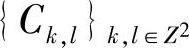的行和列作用的镜像共轭滤波器的系数矩阵，则式（4-11）可写成如下的矩阵形式：

式中，j＝0，1，...，J。二维Mallat重构算法为

C_j＝H^∗_rH^∗_cC_j＋1＋H^∗_rG^∗_cD^v_j＋1＋G^∗_rH^∗_cD^h_j＋1＋G^∗_rG^∗_cD^d_j＋1 （4-14）

式中，j＝J，...，1，0；C_j和C_j＋1是第j和第j＋1层分解图像的低频小波系数；D^v_j＋1、D^h_j＋1和D^dj＋1分别是第j＋1层分解图像的垂直、水平及对角方向的高频小波系数。低频分量反映图像的近似以及平均特性，集中了图像的大部分能量，表现物体的整体轮廓信息；高频分量反映图像的突变信息，如边缘、区域边界等。

图像经过一次二维小波变换之后得到四个子图像，其中包括一个低频分量LL₁和3个高频分量HL₁、LH₁、HH₁，其中HL₁对应水平方向高频分量，LH₁对应垂直方向高频分量，HH₁对应对角方向高频分量。如果对图像进行J次二维小波分解，J＝0时是原始图像，最终得到3J＋1个不同子图像。图4-40是图像进行两次小波分解的过程。小波分解的层次越高，其对应的子图像尺寸越小，从而形成塔式图像。

图4-40 图像进行两次小波分解过程

小波变换属于多尺度分析，而根据视觉心理和生理实验，多尺度分析存在于人眼视觉的底层信号处理过程中，因此小波变换具有和人眼类似的性能，适用于图像融合。小波的分解过程即将原图像分解成各个频域上的子图像，再根据不同分量的不同融合进行融合，从而实现更好的融合效果。

基于小波变换的图像融合算法如图4-41所示，具体步骤如下：

1）对待融合的源图像进行小波分解，得到各分解层的高频子图像和低频子图像。

2）分别对各分解层的高频小波系数和低频小波系数采用不同的融合规则进行融合，得到融合后的各层高频小波系数和低频小波系数。

3）对融合的系数进行逆小波变换，得到重构图像。

基于小波变换的图像融合算法的优势体现在三方面：第一，多分辨率分解提供了不同分辨率下图像的信息，并且变换后的能量大部分集中在低频部分，便于在对应分辨率下进行信息融合，并且可以根据需要有选择地增强某分辨率的图像特征；第二，小波分解和重构算法是循环使用的，易于硬件实现；第三，便于并行处理和实现。

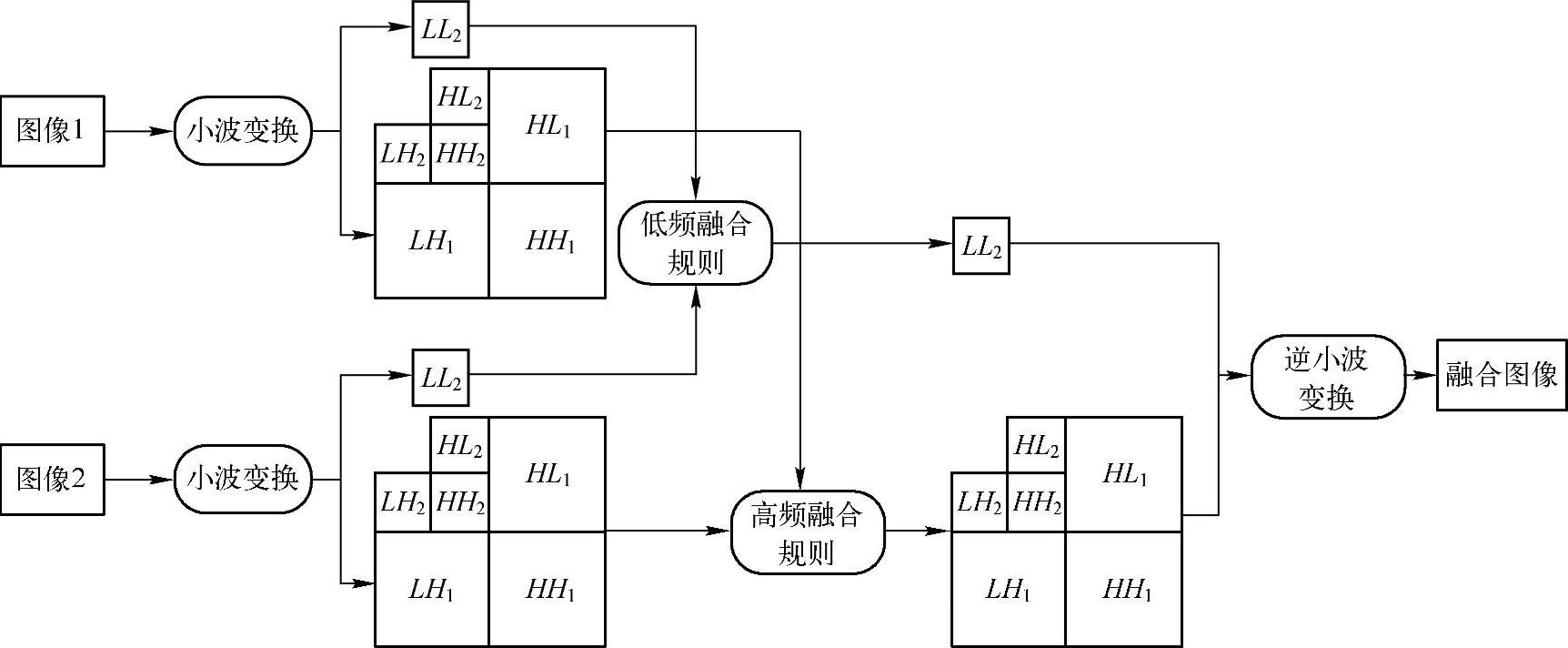
图4-41 基于小波变换的融合算法