运动分量补偿直接抑制方法

回顾性脱机门控法可以有效地抑制IC-OCT图像序列中由心脏运动所致的运动伪影，但是由于在每个心动周期只保留一帧，因而可能丢失很多具有诊断价值的血管信息。本节介绍一种对覆盖多个心动周期的非门控IC-OCT图像序列直接进行刚性运动伪影的定量估计和补偿的方法。

IV-OCT图像序列相邻帧之间的刚性运动参数如图4-27所示，在连续回撤导管采集的IC-OCT图像序列横截面视图中，不同帧中的血管腔轮廓之间存在偏移和扭转，这是由血管腔不规则的几何形态和周期性心脏运动共同作用产生的。图中Δx、Δy和Δα分别是从t₁到t₂时刻管腔重心在x方向上的位移、y方向上的位移和旋转偏移量（即旋转角度）。成像导管始终位于图像中心，管腔内膜轮廓重心在不同时刻的位置变化能够反映血管壁的运动情况。（Δx，Δy，Δα）可以表示为

其中，脚标d和g分别表示心脏运动分量和血管几何分量。与由心脏跳动引起的管腔轮廓的形态变化相比，由血管本身的不规则几何形态引起的管腔轮廓变化较为缓慢，因此可以通过滤波将其分离开，并对运动分量（Δx_d，Δy_d，Δα_d）加以补偿，实现抑制刚性运动伪影的目的。

基于以上原理，本节介绍的运动分量补偿法抑制运动伪影的具体步骤如下：

（1）提取各帧图像中的血管腔内膜轮廓并计算其重心

如4.3节所述，对于血管内OCT图像中血管腔轮廓的提取，目前的研究热点是全自动的方法。图4-28是采用文献［17］中提出的方法对一帧IV-OCT图像提取血管内膜轮廓的结果。

将管腔内膜轮廓的几何中心作为其重心的近似，假设第i帧图像中内膜轮廓点的总数为N_i（i＝1，2，…，n，n为IV-OCT图像序列的总帧数），各轮廓点在图像平面二维坐标系中的坐标为（x_j，y_j）（i＝1，2，…，N_i），则内膜轮廓的重心C_i的坐标为

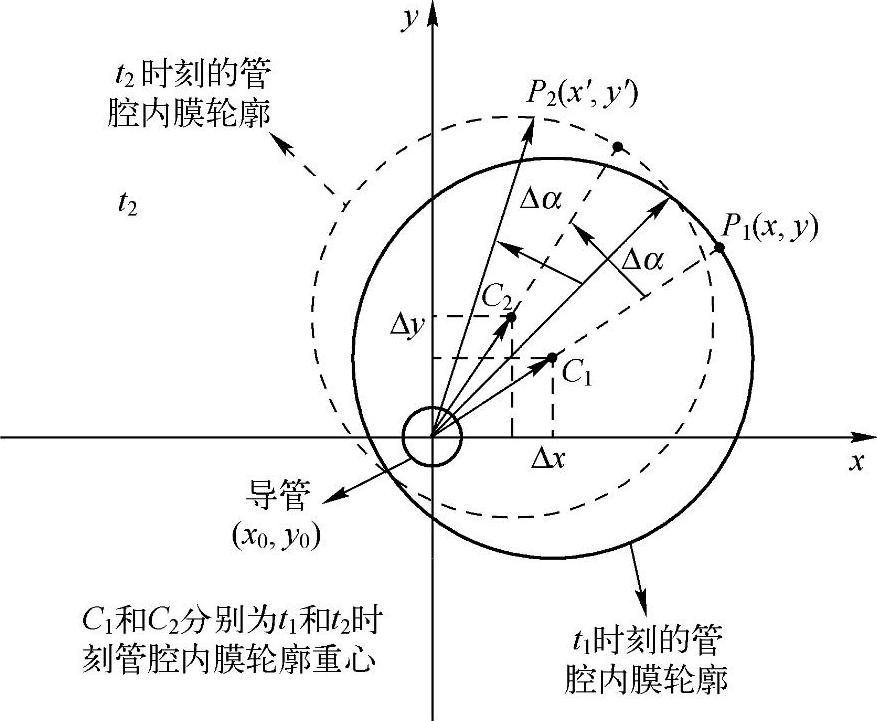
图4-27 IV-OCT图像序列相邻帧之间的刚性运动参数示意图

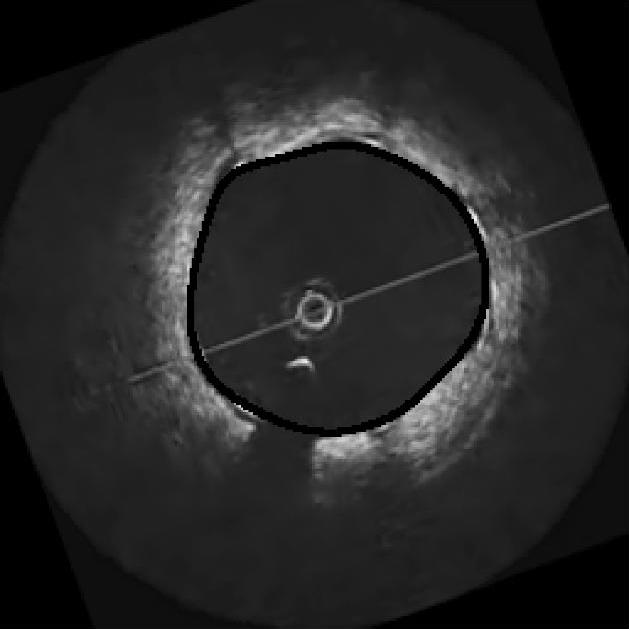
图4-28 一帧IV-OCT图像的血管壁内膜轮廓提取结果

（2）计算相邻帧之间管腔内膜轮廓的旋转偏移量

重心角示意图如图4-29所示，管腔轮廓重心C的坐标为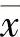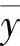（ , ），则重心角为

图像序列的重心角变化曲线α（i）（i＝1，2，…，n）应呈近似周期性的变化。通过相邻帧之间的管腔轮廓重心角之差如下：

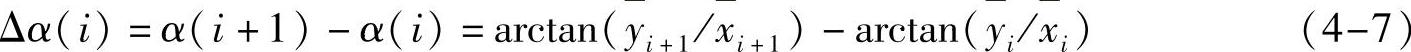
得到旋转偏移量Δα（i）。与各帧与首帧重心角之差相比，相邻帧重心角之差可准确反映出图像序列中的管腔轮廓随导管回撤的变化情况。旋转偏移量的频谱中处于45～200Hz范围内的峰值即为平均心率R。

一个原始IC-OCT图像序列的纵向视图如图4-30所示，其采集速率为10f／s，长度为100帧，从该图像序列计算得到的重心角变化曲线α（i）（i＝1，2，…，100）的时域波形和幅度谱曲线如图4-31所示，显然该曲线呈近似周期性的变化。相邻帧管腔轮廓旋转偏移量Δα（i）的时域波形和幅度谱曲线如图4-32所示。在图4-31b重心角的幅度谱曲线中，低频成分为由血管自身形态变化所致的频率成分，高频成分则为由心脏运动所致的频率成分，其峰值对应的频率即为平均心率R。由图4-32b可以看到，旋转偏移量的幅度谱曲线有一个明显峰值，其频率与图4-31b的峰值频率相等，即为平均心率R，此外还存在大量非心动频率成分。

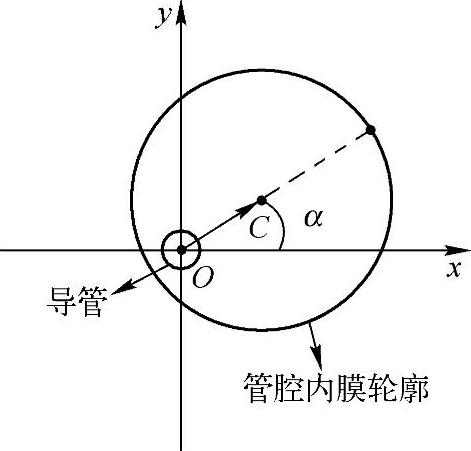
图4-29 重心角示意图

图4-30 原始IV-OCT图像序列的纵向视图

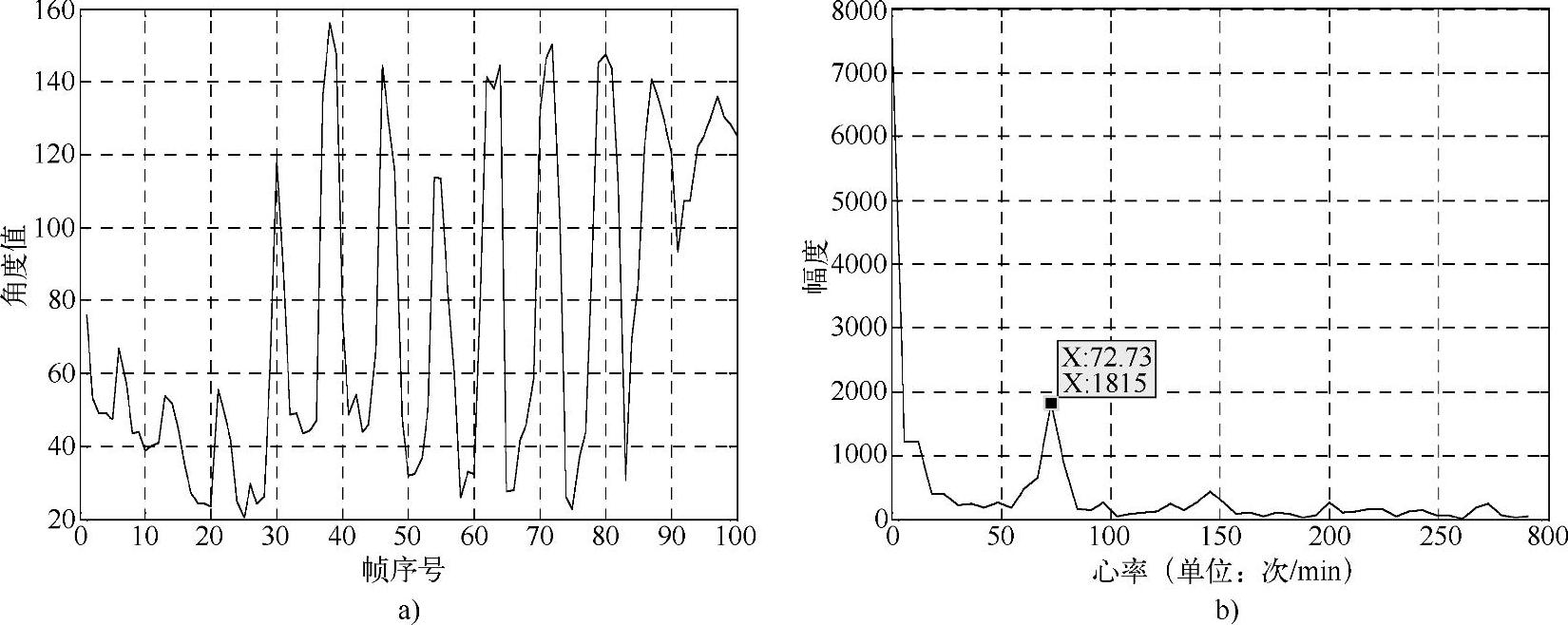
图4-31 重心角变化曲线

a）时域波形 b）幅度谱曲线

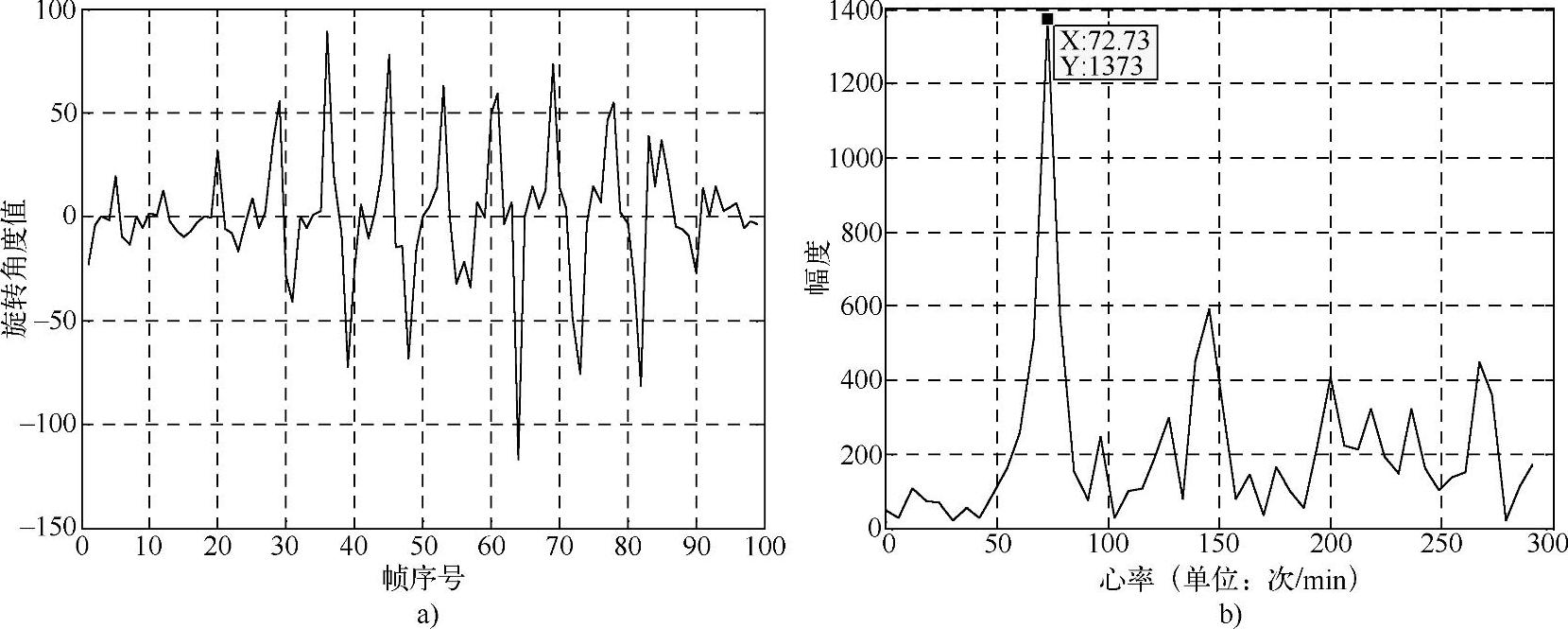
图4-32 相邻帧管腔轮廓的旋转偏移量

a）时域波形 b）幅度谱曲线(www.xing528.com)

（3）提取并补偿旋转偏移量中的心脏运动分量

旋转偏移量Δα（i）为近似周期的信号，其频谱中的高频成分为心脏运动所致的分量，低频分量则对应血管的几何形态分量，此外还有大量其他非心动频率成分，可采用带通滤波器将心脏运动分量滤出，其通带中心频率设定为第4.4.2节的步骤2得到的平均心率R，通带宽度可设为0.6R。图4-32的旋转偏移量滤波后的时域波形和幅度谱曲线如图4-33所示，可以看出经过滤波后100Hz以上的频率成分被滤除，只保留了心动速率范围（即51～94Hz）内的频率分量。

补偿旋转偏移量中的心脏运动分量，实质上就是对每帧图像进行反向旋转，变换矩阵为

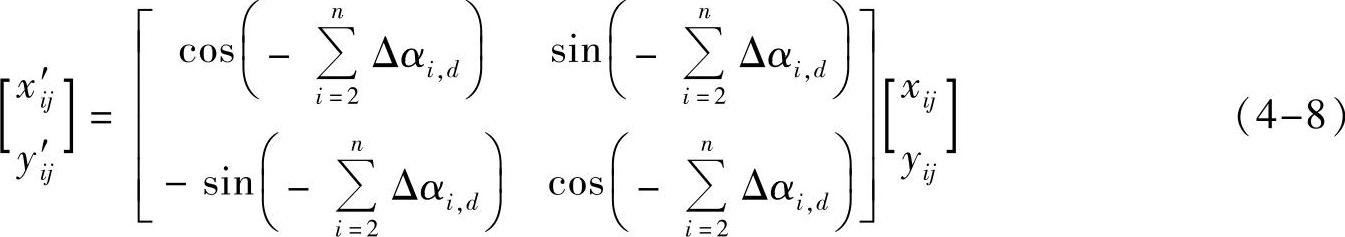
式中，（x_ij，y_ij）为第i帧IV-OCT图像序列中内膜轮廓的第j个点的坐标；（x′_ij，y′_ij）为点（x_ij，y_ij）补偿后的坐标；j＝1，2，…，N_i，N_i为第i帧图像中管腔内膜轮廓的总点数；i＝2，3，…，n，n为图像序列的总帧数。后一帧图像相对于前一帧图像进行偏转，因此应该从第二帧开始遍历，即i的取值从2开始。

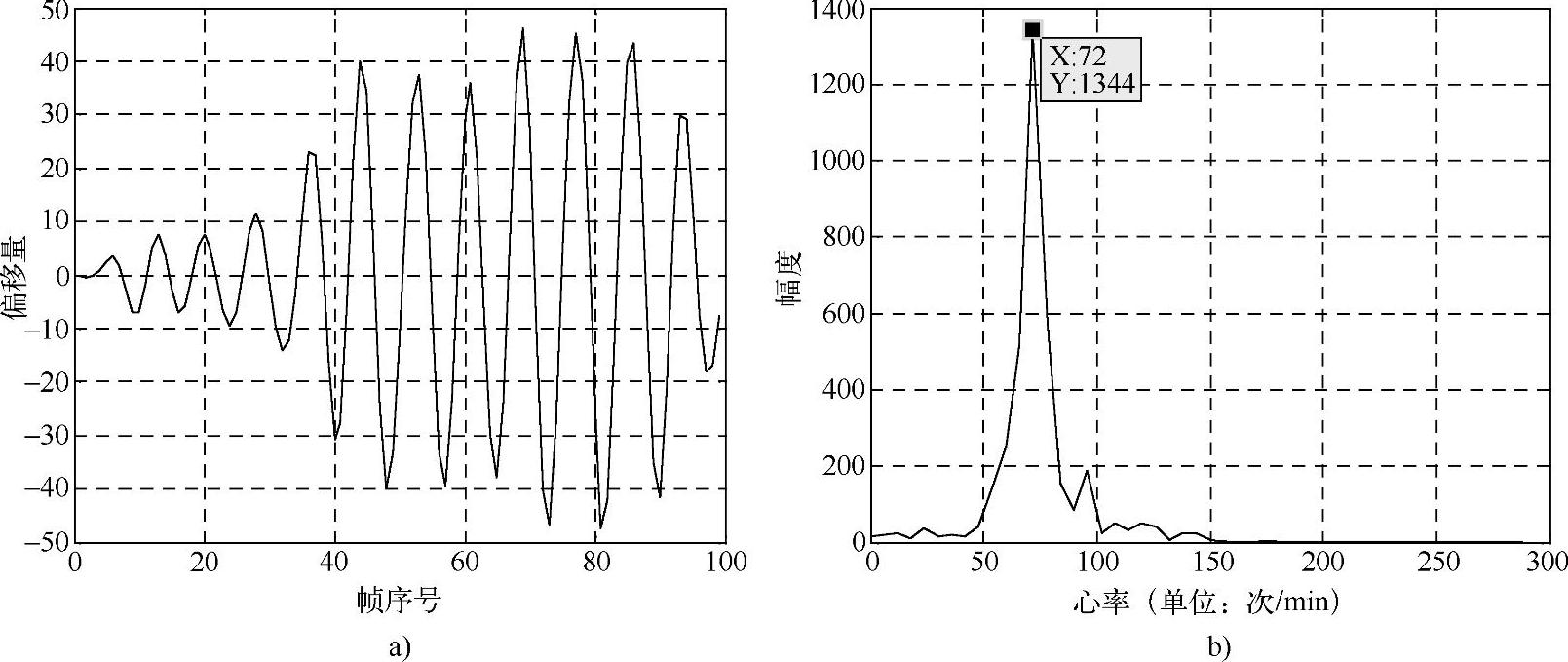
图4-33 旋转偏移量滤波后的波形

a）时域波形 b）幅度谱曲线

图4-29所示的原始纵向视图与对旋转偏移量进行补偿后得到的纵向视图的对比如图4-34所示，可以看出补偿旋转偏移量后的血管壁较补偿前变得平滑。

（4）计算补偿旋转角后相邻帧之间管腔轮廓重心的平移量

对于第i帧（i＝2，3，…，n）图像，补偿旋转角之后，首先根据式（4-5）重新计算各帧图像管腔内膜轮廓重心坐标，并得到相邻帧之间管腔重心的平移量Δx（i）和Δy（i）。然后，取Δx（i）和Δy（i）的频谱中位于［45，200］范围内的峰值，

图4-34 纵向视图对比

a）补偿旋转偏移量前 b）补偿旋转偏移量后

分别记为R′_x和R′_y。最后，对Δx（i）和Δy（i）进行带通滤波，滤波器的中心频率分别为R′_x和R′_y，带宽分别为0.6R′_x和0.6R′_y。补偿旋转角后相邻帧之间管腔重心的平移量变化曲线及其幅度频谱如图4-35所示，显然Δx（i）和Δy（i）的频谱在78.79Hz处均有一个明显的波峰。

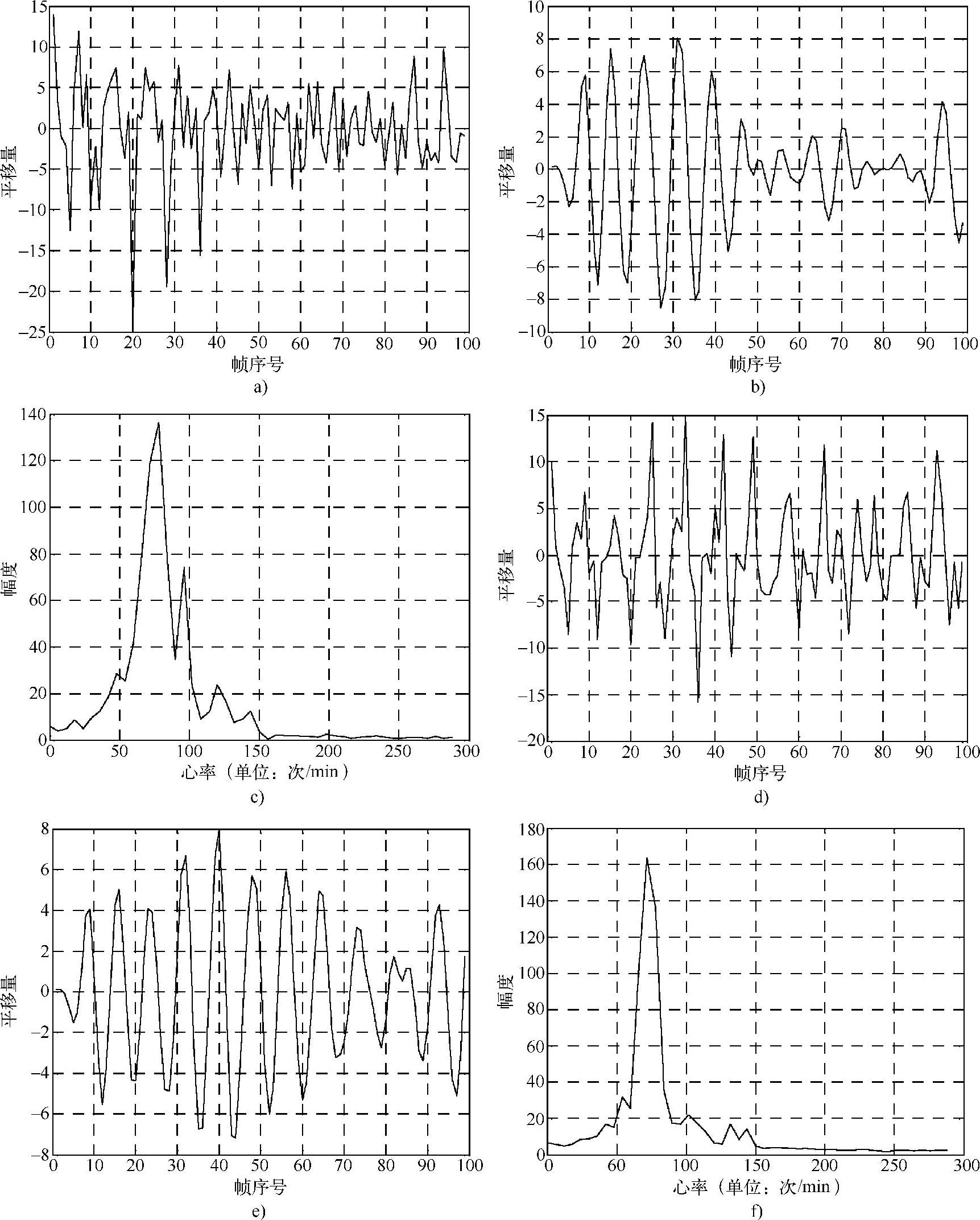
图4-35 补偿旋转角后相邻帧管腔轮廓重心的平移量变化曲线和幅度谱曲线

a）滤波前的横坐标变化曲线 b）滤波后的横坐标变化曲线 c）滤波后横坐标变化曲线的幅度谱 d）滤波前的纵 坐标变化曲线 e）滤波后的纵坐标变化曲线 f）滤波后纵坐标变化曲线的幅度谱

（5）分离并补偿由心脏运动引起的平移分量

对平移量中的心脏运动分量进行补偿，公式如下：

式中，（x′_c，y′_c）为补偿后管腔轮廓重心的坐标；i＝2，3，…，n，n为图像序列的总帧数。

由于在空间域中图像平移的最小单位为1个像素（即平移量为整数），而计算得出的平移量大部分为非整数值（亚像素值），因此不能在空间域中直接对图像进行平移，可以在频率域中实现，即首先对图像进行傅里叶变换，然后进行相位平移，最后对平移后的频域图像进行傅里叶逆变换。

补偿运动伪影前后的IC-OCT图像序列纵向视图如图4-36所示，其中图4-36b为对图4-30所示的IC-OCT图像序列的运动伪影补偿结果，可以看出补偿运动伪影后纵向视图的视觉效果得到了很大改善，抑制了血管壁的锯齿效应，血管壁边缘变得平滑。

图4-36 补偿运动伪影前后的IC-OCT图像序列纵向视图

a）原始纵向视图 b）补偿运动伪影后的纵向视图

完成对运动伪影的抑制后，IC-OCT纵向视图中血管壁的边缘变得相对平滑，结合X射线血管造影提供的导管空间位置信息，即可重现血管的空间三维结构。