基于三维血管模型的血管壁局部应力应变估算方法

利用重建出的三维血管模型，采用基于计算流体动力学（Computational Fluid Dynamics，CFD）的数值模拟技术，可对由血流引入的冠状动脉血管壁剪切应力的分布情况进行估算。其基本原理是：首先对冠状动脉管腔内的血液流动建立数学模型，通常是用Navier-Stokes方程来模拟血液在血管腔中的流动，并且不考虑动脉血管中的热量和其他能量形式的交换问题；然后使用CFD商用软件（例如基于有限体积法的FLUENT）对由于血流引入的WSS分布进行数值模拟，求解控制方程，求解过程主要包括构建物理模型并划分网格、设置求解参数、计算模型初始化、计算求解、结果收敛性、正确性检查等步骤。

（1）建立动脉血管的流固耦合数学模型

考虑到血液流场与动脉血管壁耦合的过程非常复杂，一般在以下假设前提下进行三维流固耦合计算：

1）所研究的动脉血管的直径都大于1mm，这类血管中的血液可以看做是均匀的连续介质，即可近似认为是不可压缩的牛顿流体。

2）血液的流动为定常层流。

3）动脉血管壁是线弹性的且不可压缩。

4）忽略血液的重力。

5）忽略温度的影响，即不研究温度和流动以及应力的耦合，不考虑血管中的热量和其他能量形式的交换问题。

采用Navier-Stokes方程

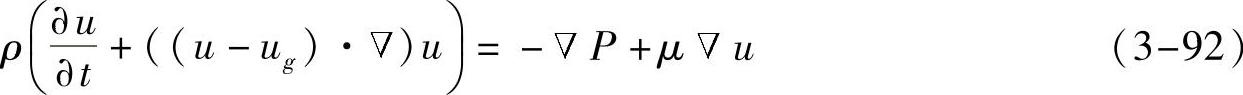
和速度散度为零的连续方程（即不可压缩方程）

▽.u＝0 （3-93）来描述粘性不可压缩的血液流体的流动。式中，ρ和μ分别是血液的密度和粘度；u和P是流体的速度和压力；u_g是网格点速度；t是时间。

定义分析区域即血液流体部分具有光滑边界，血流的进、出口速度边界条件如下：

式中，interface为血管壁内表面；inlet和outlet分别为入口和出口；行为边界上的单位外法线向量。入口的速度矢量沿血管轴线方向，径向和周向速度均为零。

设置血流的进／出口的压力边界条件为压力随时间变化的函数如下：

采用独立的拉格朗日一欧拉方程作为血管壁的运动方程，公式如下：(www.xing528.com)

血管壁的应变一位移关系为

式中，i，j=l，2，3；p_s、u(u_i，u_j)、σ_ij和ε_ij分别是血管壁的密度、位移向量、应力张量和应变张量：f_i是作用在血管壁上的体力分量；x_j是三维直角坐标系中三个坐标轴的正方向。

血管壁的内表面为流固相互作用的界面，即耦合面，公式如下：

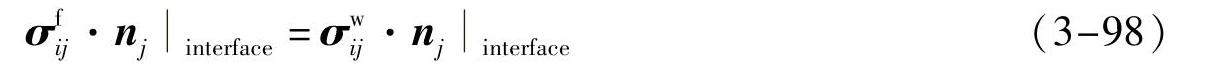
式中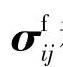， 和 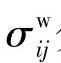分别是血液和血管壁的应力张量血管壁的外表面是自由面，公式如下：

(2)CFD数值模拟

在ANSYS Workbench T作平台上，采用ANSYS+FLUENT单向流固耦合模块，对心动周期中各时刻的子维血管及血液模型进行血液和血管壁的流固耦合数值模拟，估算血管壁的应力／应变张量。基本步骤如下：

1)划分有限元网格。三维血管和血液模型是非对称的，且几何形状非常复杂，因此在网格划分过程中很难划分㈩特别规范的均匀网格。同时，对于狭窄段，也很难保持原有规范的网格形状。因此本书采用智能型的网格划分模式，将血液与血管的三维几何模型离散化，在遇到形状突变时，能按照合理的划分方法自动加密，以获得更加理想的网格单元。

2)建立三维血管有限元模型。设定初始条件，即定义血管和血液的物理属性，典型参数见表3-3，其中各参数均取人体正常生理条件下的平均值。考虑到粘弹性材料可能使流固耦合的迭代计算不收敛，因此可不考虑血管的粘弹性。设置温度为37。c。设定边界条件，即对血管模型的入口和出口设置为固定约束，限制血管内血液的流动范围。对于同体部分，血管外壁面只设置一个自由壁面条件，不加其他约束限制；血管内壁面（即血流与血管接触的内表面）设定为流固耦合界面，并假定无滑移边界条件（对于定常层流，假设管壁上流体质点的流速为零：对于不定常层流，假设管壁上流体质点的速度和管壁速度相同）。对于流体部分，将边界条件设定在血流进出口界面上，出口压力设定为零。设定血液流动的载荷，就是血管入口处给定的流体速度。为了实现流固耦合中数据的传输，将血液对血管壁的压力作为加载流，将血管腔内表面上所有的流体动力都加载到血管壁内表面上。定义时间步长、设定求解开始的时间、选择迭代求解方法、设置收敛准则、误差要求、输出信息控制等。

表3-3 人体血管、血液和脉搏参数

3）对计算结果进行后处理。为了提高计算结果的可视化效果，用伪彩编码显示估算出的血管壁应变张量分布以及瞬态的流场变化，直观展示由于搏动的血液及周期性心脏运动引起的血管壁应变的三维分布。

此类方法可直观地展示血管的三维形态结构和应力应变分布情况。但其不足之处在于，WSS测量结果的精度很大程度上取决于血管三维重建的精度。重建过程中，图像采集、二维分割、确定各帧IVUS图像的轴向位置和空间方向等步骤中存在的误差都会累积在最终的重建结果中，进而影响对血流动力学参数的测量精度。由于无法得到人体冠脉血管的真实形态，因此很难定量评价三维重建结果的精度。同时由于需采用CFD软件进行数值模拟分析，因而提高了方法的应用前提，限制了其适用范围。