斑块体积与厚度分析

斑块的体积反映了病变的程度，可作为评价病变进展和消退情况的重要指标。粥样硬化斑块的形状是不规则的，如图3-99所示，所以可采用体积微元的思想通过划分体积网格求解该不规则区域的体积。血管壁网格化示意图如图3-100所示，在图3-100a中，先计算内腔-斑块边界与外膜边界之间的各个网格体元的体积V_k，那么目标区域的体积V就是这些网格体元的体积之和，公式如下：

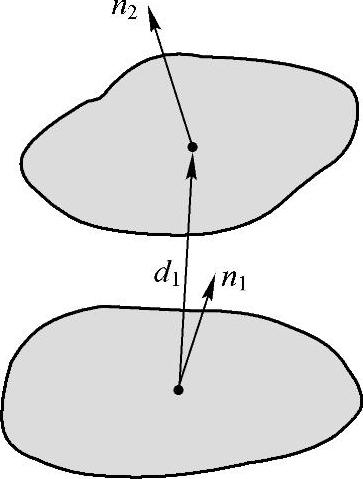
图3-98 血管段上下截面示意图

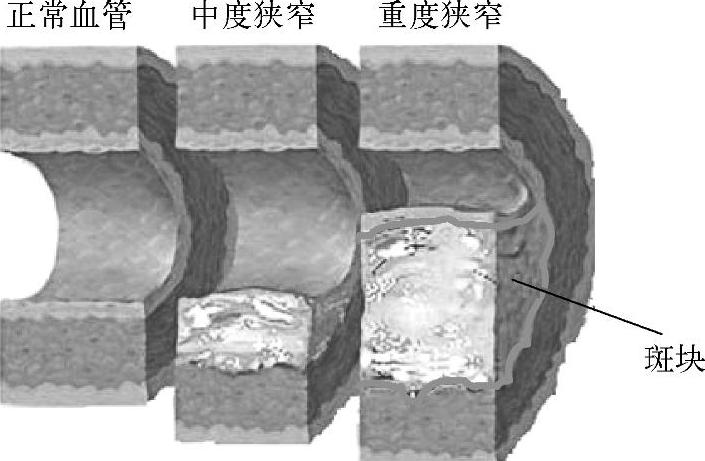
图3-99 冠状动脉粥样硬化斑块示意图

如图3-100b所示，图3-100a中网格体元的构成方法如图3-100b所示，具体过程如下：

1）以管腔轮廓的几何中心作为对其重心的近似，得到血管段上下截面（即相邻两帧IVUS图像）中血管内腔轮廓的重心C_L2和C_L1。

2）在前一帧图像的管腔轮廓上任取一点A作为起始点，使其与重心C_L1的延长线与外膜相交于点B。由两条直线可确定一个平面，可知C_L1B与i_L1C_L2两条直线确定的平面与第二帧超声图像内、外膜轮廓分别相交于点E和F，则ABCDEFGH就构成了一个六面体网格体元。

3）若要划分的体元数为n，则以A为起始点在内膜轮廓等间隔地取n个点A_i（i＝1，2，…，n），以A_i代替A重复步骤2，求这些点在其外膜轮廓和下一帧超声图像上对应的点B_i、E_i和F_i（i＝1，2，…，n）。

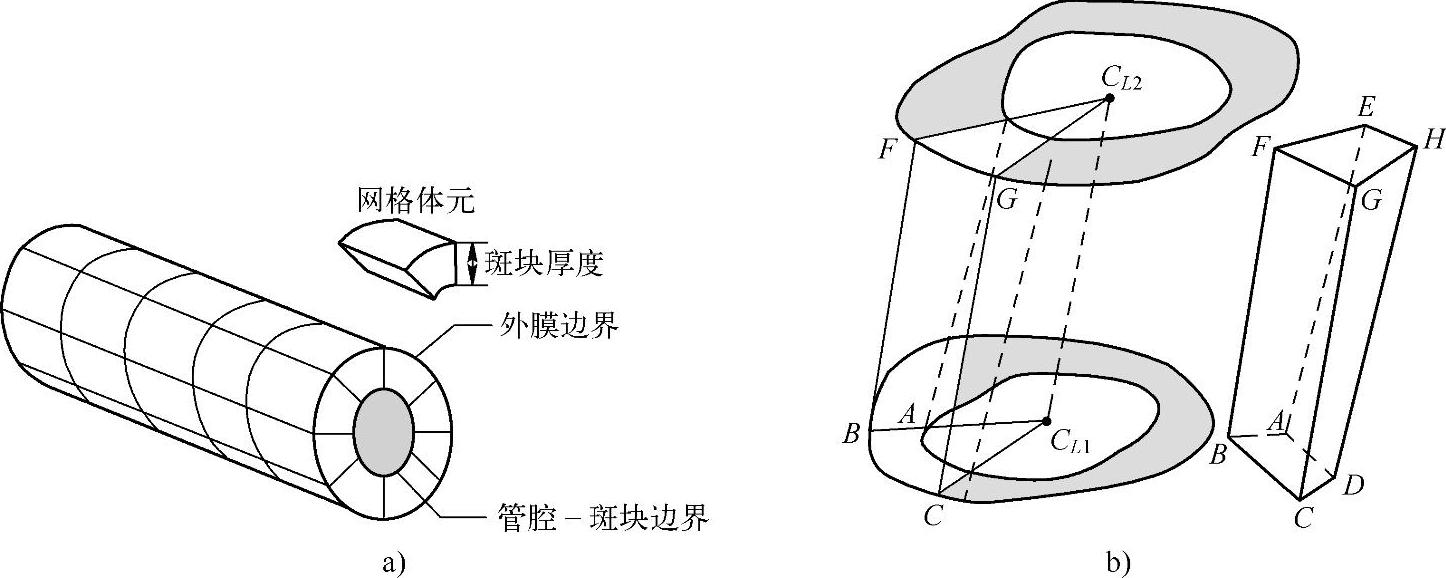
图3-100 血管壁网格化示意图^［95］

a）网格化的三维血管段 b）体元的构造方法

目前计算体元体积的常用方法有三种：多胞（polytope）法、Watanabe法和Simpson规则法^［95］示意图如图3-101所示。

（1）多胞（polytope）法(www.xing528.com)

在图3-101a中，每个体元是由8个顶点构成的多面体，该多面体有6个面，每个面包含4个顶点。绕顶点逆时针转动时，其法向量指向外。从任意顶点V₀开始可以获得一个顶点的有序序列｛V₀，V₁，V₂，V₃｝，构成两个三角形V₀V₁V₂和V₀V₂V₃，每个三角形和坐标原点O都构成一个四面体。对于体元的每个表面，都计算出各四面体的体积，然后相加即可求出体元的体积，其公式如下：

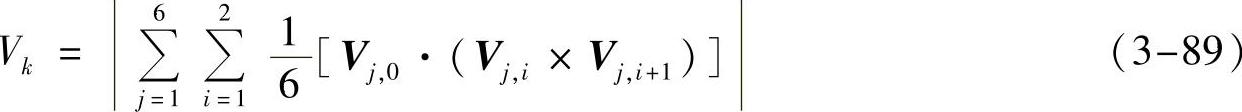
式中，V_j，i表示坐标原点O与第j个表面上的第i个三角形的顶点之间的向量。

（2）Watanabe法

在图3-101b中，首先分别计算出多面体的下表面ABCD和上表面EFGH的重心C_bottom和C_top，及其法向量n_t和n_b，两重心之间的向量为d＝C_top-C_bottom，则多面体的体积为

（3）Simpson规则法

按照图3-101c构造由连续三个切片构成的体元，其上、中、下表面的重心分别为C_top、C_mid和C_bottom，法向量分别为n_t、n_m和n_b，定义向量d₁＝C_mid-C_bottom和d₂＝C_top-C_mid，d＝d₁＋d₂。则多面体的体积为

与Watanabe法相比，该方法采用的体元扩大了一倍。

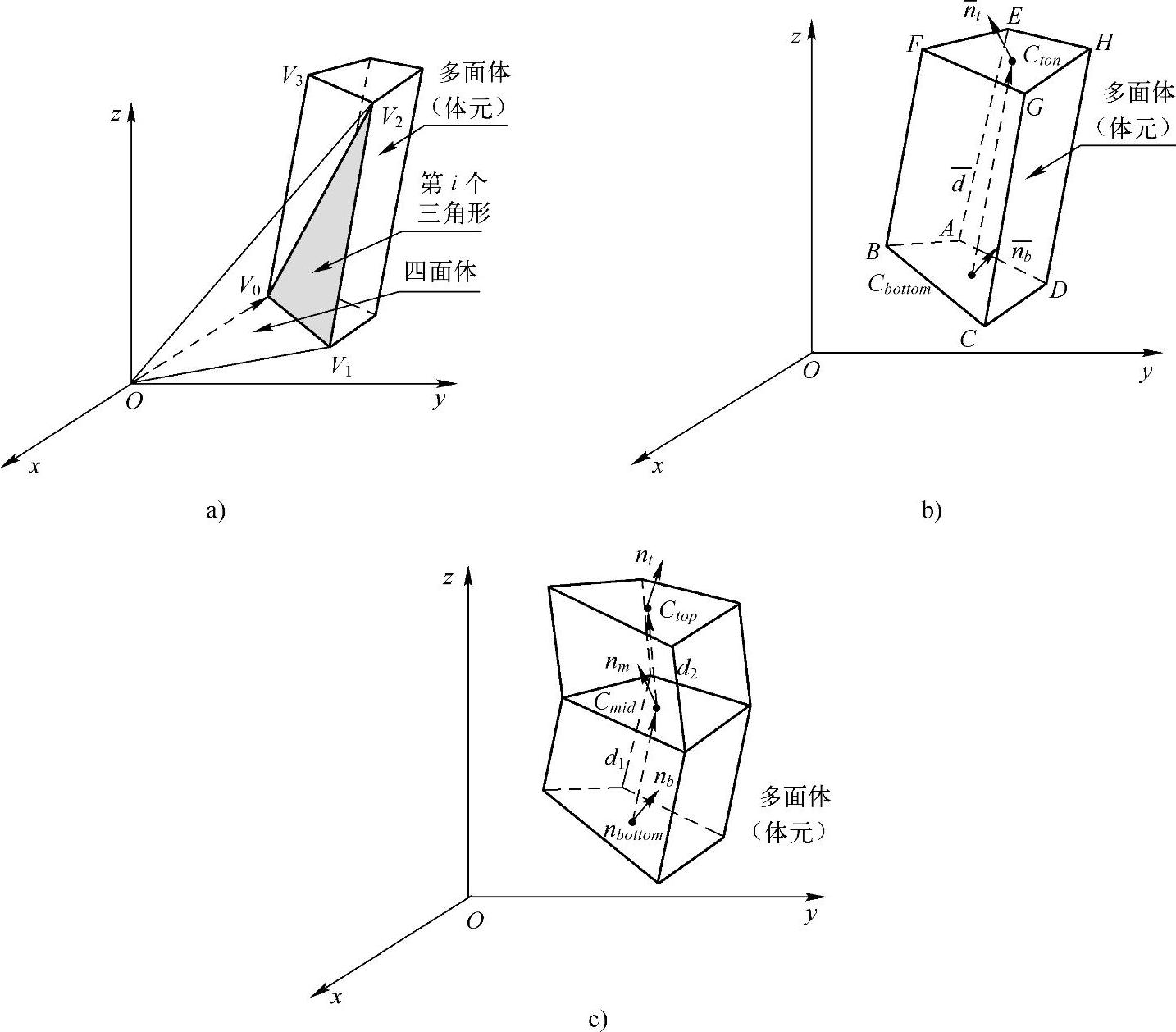
图3-101 体元体积计算示意图^［95］

a）多胞法示意图 b）Watanabe法示意图 c）Simpson规则法示意图

对于每帧IVUS图像，利用分割出的斑块-内腔和斑块-中膜边界，连接管腔横截面的重心和斑块-中膜边界上的一点A，所得线段与斑块-内腔边界交于一点B，线段AB的长度即为点A（或B）处斑块的厚度。相对于斑块的绝对厚度值而言，斑块的分布对于临床诊断的意义更大。