含钙化帧的弹性配准方法优化

冠状动脉附着在心外膜表面上，在冠状动脉内超声图像的采集过程中，由心脏运动引起的血管移位以及血管曲率和管腔直径的改变，都会导致各帧IVUS图像之间很难保持空间上的一致性。为了保证IVUS图像中血管壁边缘的检测、血管形态参数的定量测量以及血管三维重建等的准确性，必须对由心脏运动引起的图像错位进行纠正。本节介绍对含钙化斑块帧进行弹性配准的方法，以钙化点作为标志点，寻找血管壁之间的空间映射和对应关系，使IVUS图像序列实现空间上的一致性。

基于标志点的IVUS图像弹性配准流程图如图3-56所示，首先采用特征描述算子对标志点的特征进行描述，然后采用薄板样条插值法寻找两幅图像中标志点对之间的对应关系，进而计算血管区域之间的空间变换关系。

图3-56 基于标志点的IVUS图像弹性配准流程图

（1）提取血管壁轮廓

从各帧IVUS图像中提取出血管壁的内、外轮廓。基本步骤包括：首先，对图像进行各向异性扩散滤波；然后，对滤波后的图像计算灰度梯度分布图，如图3-57所示；其次，根据IVUS图像的大小以及图像中血管壁所在的区域，将snake初始轮廓设置为以图像中心为圆心、半径为25个像素大小的圆；最后，根据滤波后图像反映的具体信息，对snake模型的初始轮廓进行平滑演变，最终得到血管壁的轮廓曲线。

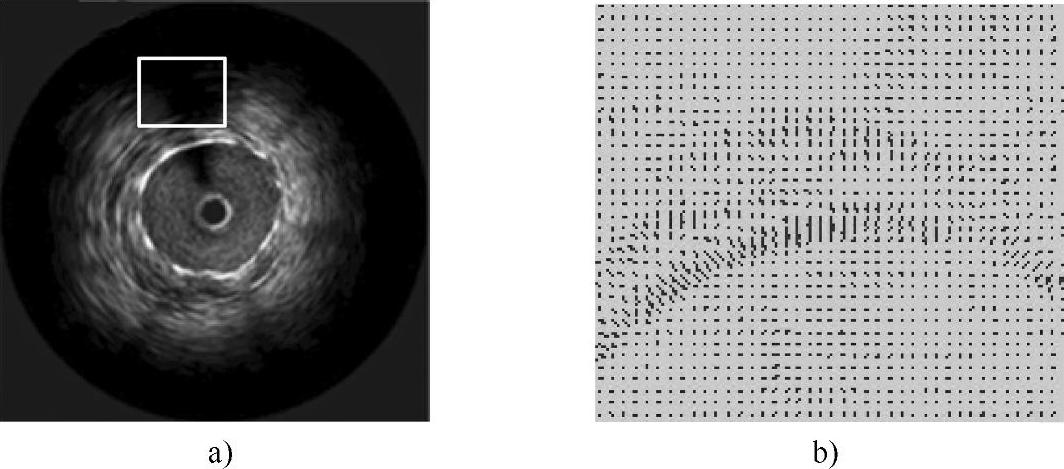
图3-57 图像的灰度梯度分布

a）一帧典型的IVUS图像 b）图a）中矩形区域的灰度梯度分布

（2）提取血管壁轮廓特征点

由于IVUS图像中钙化斑块的位置全部集中于血管腔附近，因此需从血管腔轮廓曲线上提取特征点。首先，将提取出血管壁轮廓的IVUS图像进行极坐标变换，如图3-58a所示，并标出血管壁轮廓线上钙化斑块区域所占的轮廓段，如图3-58b所示；然后，在斑块所在轮廓段上随机抽取若干不同点对，并存储其坐标，为下一步配准所用。

图3-58 IVUS图像的极坐标视图

a）轮廓图像的极坐标表示 b）钙化斑块区域的血管壁轮廓

（3）描述特征点

提取特征点之后，只知道它们在图像中的位置信息，并不具有足够的独特性和可识别性。为了使特征点能够充分反映出IVUS图像的结构特征，还需采用恰当的描述算子对特征点周边邻域的局部信息进行描述。

理想的特征点描述算子应该具有鲁棒性和独特性，即所采用的描述算子应该对于图像的几何形变和失真具有不变性，并且可以通过计算同类描述算子之间的差别对特征点之间的相似度进行定量测量。这里介绍两种特征点描述算子：二维描述算子和一维描述算子。

常用的特征描述算子主要包括灰度、形状、纹理以及空间约束关系等。其中空间约束关系是非常重要的视觉特征，最常见的空间约束关系特征是相关图。不同于灰度直方图，图像的相关图不但能够反映图像整体的统计信息，而且也能够反映图像中像素的空间组织信息，但忽略了像素的空间组织。

这里采用相关图法提取特征点的二维特征。基本步骤包括：首先，以轮廓上的各特征点为中心，对图像进行空间量化，如图3-59a所示；然后，根据量化空间计算该点与其他各特征点之间的距离与角度；最后，将距离与角度数据作为特征点相似度测量的二维特征向量，为下一步的配准作准备。

图3-59 特征点的二维描述算子示意图

a）以轮廓上某特征点为中心对图像进行空间量化变换 b）该特征点的二维特征信息示意图

设C为特征点集，总点数为n，其中p。为点集C中一点。以p：为中心将图像进行空间划分，设hi为该点关于其他某一点的空间相关特征向量，则危i的表达式如下‘“]：

h.(r,θ)={p_iEC,p，≠p_i：II (p_j-p_i) II ED，，（p_i-P_i)EA_θ} (3-44)

式中，D。是第r(r=1，…，n。)级距离空间；A_θ是第θ(θ=1，．，，，n。)级角度空间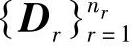； 和 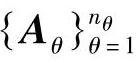分别是标志点距其他相关点距离与角度的集合

随着心脏的搏动，冠状动脉管腔内的血液对于血管壁的压力不断变化，血管腔也会随之不断地产生各种形变。特征点均位于管腔轮廓之上，因此仅使用一种特征对形变严重的冠脉血管IVUS图像进行配准，不能达到理想的效果，因而增加一种对血管腔形变具有鲁棒性的一维特征，作为对相关图的弥补。具体方法是：首先，等距离划分血管壁轮廓曲线，并统计各个特征点所处的空间次序，如图3-60所示：然后，根据标志点所处空间的不同，计算各点之间的距离：最后，将各标志点与其他各点的一维空间距离作为标志点的一维特征向量。

图3-60 血管壁轮廓特征点一维描述算子示意图

设P_i为血管壁轮廓上的第i点，u_i为P_i点的一维特征向量，因此u_i的大小等于该点在轮廓上所处长度空间的序号。设Γ:[o，1）→R²为标志点的一维特征向量函数，p_i点在一维特征向量函数中的参数为u_i，且Γ(u_i)=P_i，u_i∈[0，1)。因此对于图集C相对应的标志点的一维特征向量集为 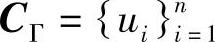。点p_i的一维特征向量如下^［65］：

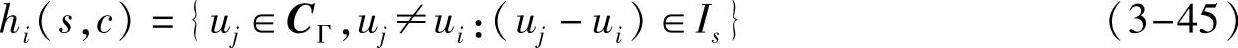
式中，I_S是第5个标志点与其他各点一维特征距离的集合，s=l，…，n_S。

(4)配准图像

常用的图像配准方法有：基于形状匹配和B样条插值的配准法、基于光流场模型的配准方法、最近距离点迭代( Iterated Closest Point，ICP)算法以及薄板样条(Thin Plate Spline，TPS)插值算法等。其中ICP算法和TPS算法是最常见的基于点特征的图像配准方法，前者常用于刚性变换情况下特征点的配准，具有计算简便、复杂度低等优点，但对形变较大的物体进行配准则效果欠佳：后者是唯一能够清楚地将映射分解为刚性映射和非刚性映射的样条函数，在保证点集之间一一对应约束的条件下，通过最小化TPS的弯曲能，联合求解点集之间的匹配矩阵和映射参数实现点集之间的弹性配准。下面介绍分别采用ICP和TPS插值算法实现IVUS图像弹性配准的方法。

ICP算法的原理是通过迭代计算特征点集的旋转和平移变换矩阵，使得来自两个点集的对应点之间的距离最小，具有计算简单、迭代速度快等优点。主要步骤包括：计算最近距离点：计算点集之间的配准变换关系；根据变换关系计算参考点集的坐标变换：计算新点集与参考点集之间特征集误差，如果小于预设的极限值，则配准结束，否则将通过变换得到的新点集作为参考点集，重复上述步骤。

假设有两个特征点集P和Q，包含点的个数都是n，P_i和q_i分别为点集P和Q中的一点，则配准特征点的目标函数如下：

使式（3-46）最小的R和T就是代表两个点集之间转换关系的旋转矩阵和平移矢量。假设R₁为符合要求的旋转矩阵，T₁为平移矢量，则理想情况下通过点p_i变换得到的对应点q_i应满足下式：

q_i＝R.p_i＋T＋N_i （3-47）

式中，N_i表示两个点之间的转换误差。

ICP算法配准过程就是求解式（3-46）的最优解的过程。为了简化点集的配准过程，降低配准的复杂度，首先要对式（3-46）进行简化，步骤如下：

1）计算参考点集与待配准点集的重心，公式如下：

根据式（3-46），显然有p＝q.R＋T。

2）计算各点与重心之间的距离，公式如下：

3）将式（3-49）代入式（3-46）得出下式：

E²＝‖q′_i-R×p′_i‖² （3-50）

4）分解式（3-50）的右端，得到下式：

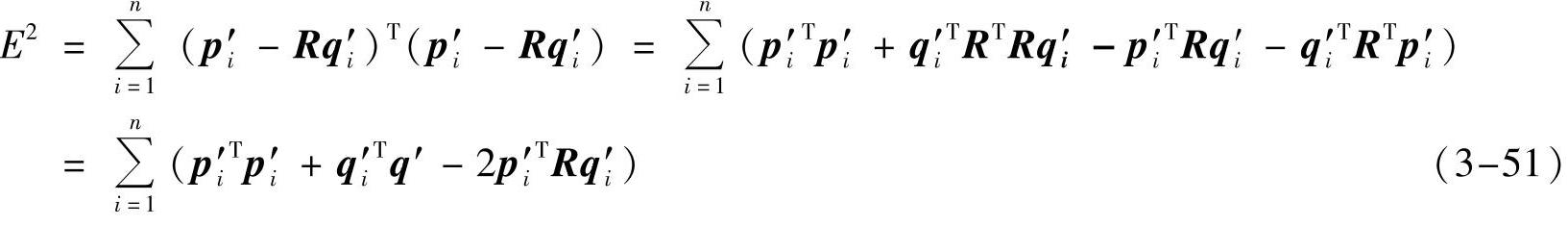
5）将求解E²最小值的问题转变为求解2p′^T_iRq′_i最大值的问题。即求下式中F的最大值：

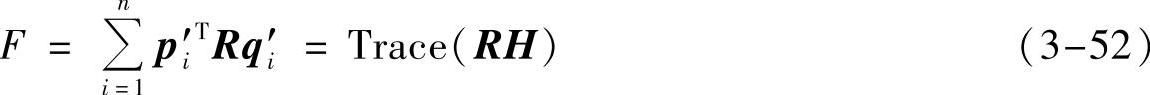
式中，

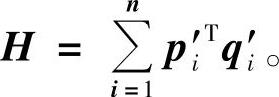
通过上述简化处理，最初的特征点配准问题演变为求Trace（RH）最大值的问题。对H进行奇异值分解得到H＝UΛV^T，其中U和V为正交矩阵，Λ为非负的对角矩阵。令正交矩阵X＝VU^T，则有下式：

XH＝VU^T UΛV^T＝VΛV^T （3-53）XH为对称正定矩阵，对于任意的正交矩阵B，有如下公式：

Trace（XH）≥Trace（BXH） （3-54）

因此可知，当R＝XH时，F值将达到最大，此时的E为最小。

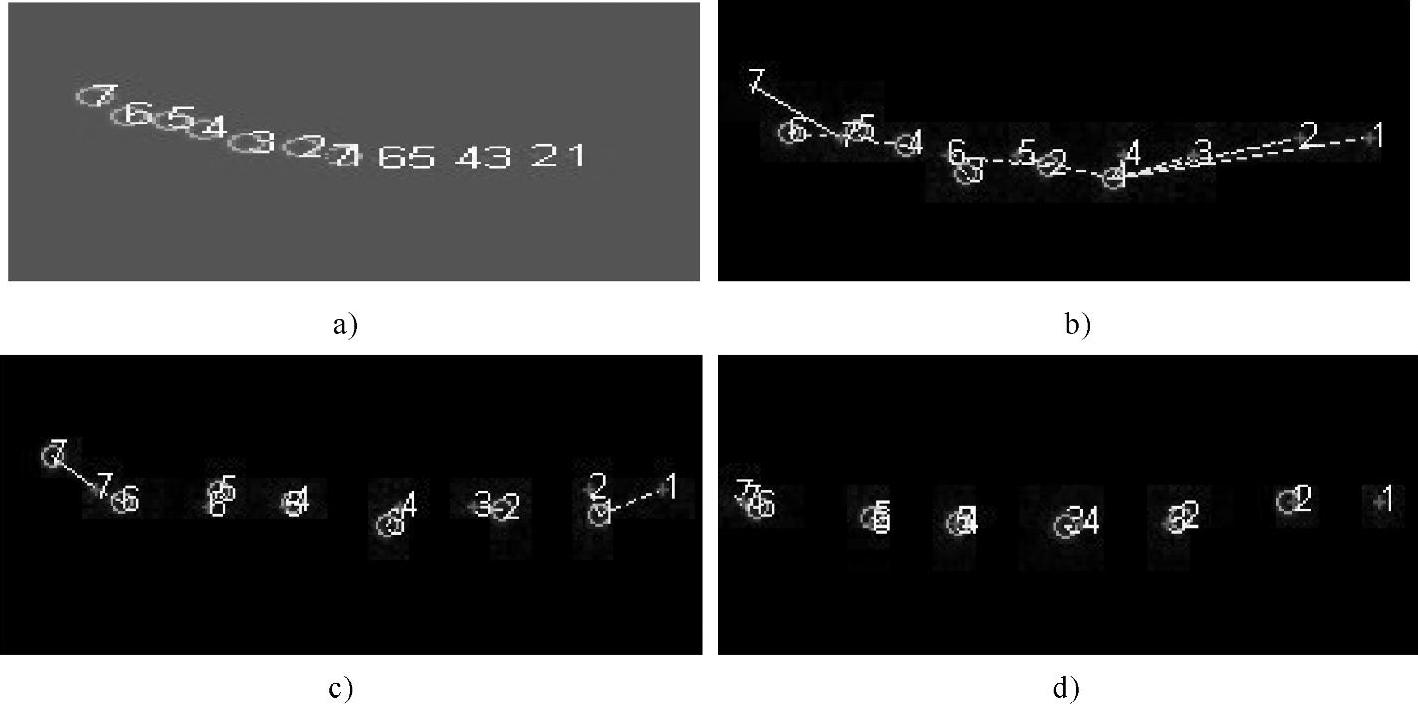
ICP算法配准过程如图3-60所示。图3-61a中绿色圆圈为参考点集，红色星号代表待配准点集，分别标出了各自的初始位置；图3-61b为采用ICP算法对两个点集进行配准的过程中，迭代25次时的结果，其中点对之间的虚线代表对应关系；图3-61c为迭代75次时的配准结果；图3-61d为最终的配准结果，迭代次数为100次。由图3-61可以看出，当点集之间的空间关系为非刚性时，使用ICP算法的效果并不理想。根据ICP算法的原理可知它只是计算对应点之间的局部最小值，但并不约束点与点之间的一一映射关系，即配准的结果可能会出现奇异点的情况，图3-61d中的点1在没有对应点的情况下成为奇异点。

(www.xing528.com)

图3-61 ICP算法的配准过程

a）参考点集与待配准点集的初始位置 b）经过25次迭代后两点集的空间位置 c）经过70次迭代后两点集的空间位置 d）两点集最终的匹配结果

TPS插值配准方法分为两部分：一是确定配准的迭代过程，二是确定每次迭代过程中待配准点集的坐标变换函数。

图像配准的目的是找到参考图像与待配准图像之间点与点的一一对应关系。假设参考图像与待配准图像分别用两个点集V＝｛v_a∈V，a＝1，2，...，K｝和X＝｛x_i∈X，i＝1，2，...，N｝表示，二者点与点之间的配准关系定义为z，即当点v_a与x_i是对应点时，z_ai＝1，如图3-62所示。

将两幅图像的弹性变换函数定义为f，因此点v_a根据变换函数经过一次迭代之后的位置为u_a＝f（v_a）。同理，点集V经过单次迭代之后转变为U即{u_a}。根据以上定义，图像配准的能量函数定义如下：

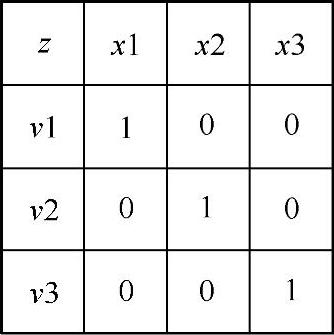
图3-62 二维点对应关系

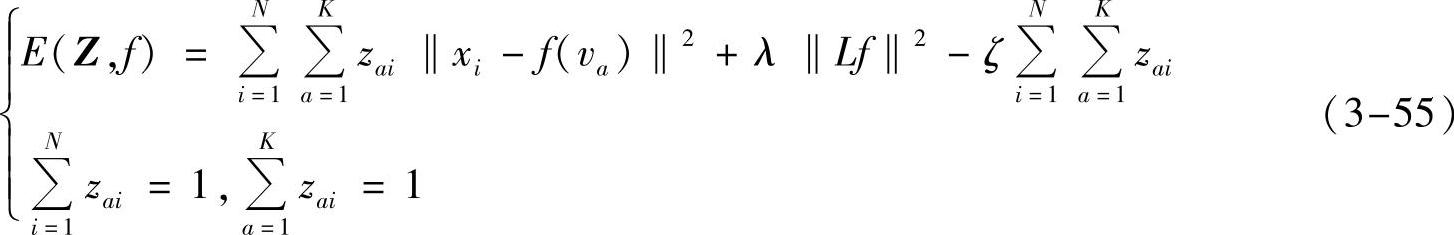
式中，L为f的约束参数；λ与ζ为权重参数。式（3-55）的第三项的作用是约束多余点的数量。矩阵Z为点集的二值对应矩阵，当点v_a与x_i是对应关系时z_ai＝1，其他为0，根据该二值矩阵可确定两个点集之间的一一对应关系。

但在实际的处理中，点对之间的匹配度往往不是理想的0和1，而是处于0～1之间。可采用扩散对应关系的方法^［66］，即将点集对应矩阵中的元素设置为0～1之间的小数，使根据对应矩阵的行与列判断两点之间的对应关系变得更具有鲁棒性。将下式加入到初始的配准能量公式中：

式中，T是温度系数，当T值较大时，约束点对之间的对应关系变得更加扩散化，逐渐减小T值的同时能量也会随之减小，点对之间的对应关系也会变得更加精确；m_ai是点v_a与x_i的对应关系系数。因此，配准能量函数变为

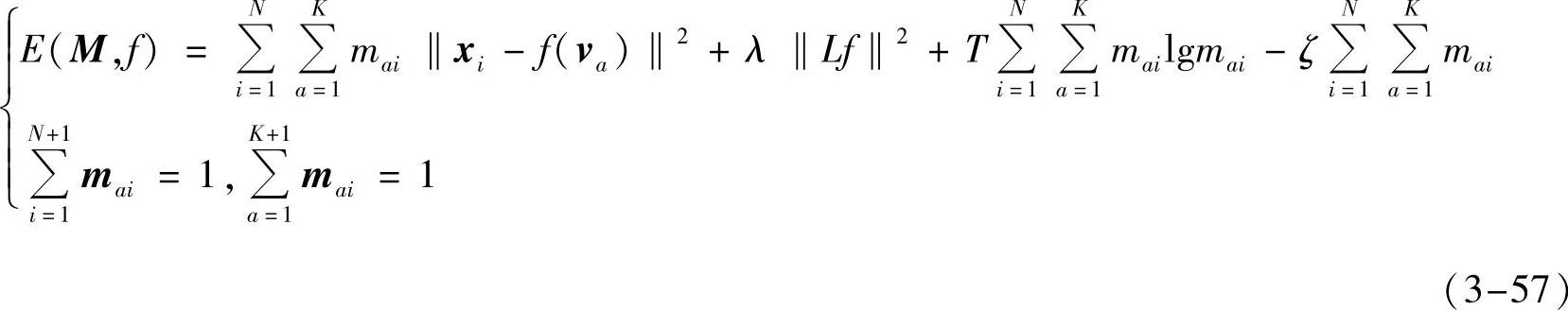
当转换约束参数T为零时，迭代结束，参考点与标志点之间的配准过程完成。扩散映射系数m_ai的计算式如下^［66］：

式中，温度系数T的初始值T₀是人为设定的，且满足T^new＝T^old.r，r为［0，1］范围内的小数。随着逐次迭代T逐渐缩小，对应系数矩阵M和变换公式f也在不断更新，当能量函数值达到最小时，点与点之间的对应关系也随之确定。

TPS插值配准方法在刚性配准中的应用已经很广泛，但是当应用于弹性配准时，必须考虑以下两个问题：

1）权重参数ζ控制着估计两个点集中奇异点数量的鲁棒性，但是并没有统一的方法能够计算出此系数的值。可将每个点集中奇异点的温度系数T设置为一个很大的值，使得奇异点形成一个集合。

2）平滑度控制系数λ的值越大对弹性变换函数的约束力越大。另一方面，减小λ的值，会使得变换更加松散、自由，同时转换关系也变得不稳定。可在迭代过程中逐次减小λ的值，即λ＝λ_initT，其中初始值λ_init为常数。

在确定图像配准的迭代过程之后，还需进一步确定每一步迭代中特征点集的坐标变换函数，即式（3-57）中的f，可采用薄板样条插值对待配准点集进行坐标变换。

薄板样条插值是一种基于点的非线性变换方法，最早由Bookstein^［67］引入医学图像配准领域。基本思想是将插值问题模拟为一个金属板在点约束下的弯曲形变，再用形变的能量以简练的代数式表示。薄板样条定义如下：^［68］

该方程的解为

式中，

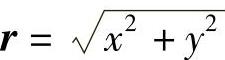
，函数U（r）是构建薄板样条的基函数。

如果用函数f（x，y）描述薄板，点（x_i，y_i）为集合中的一点，要使金属板在该点处高度为z_i，并且此时该板具有的最小弯曲能量，则f（x，y）必须使与点约束相关的积分I_f值为最小，其中I_f的定义如下

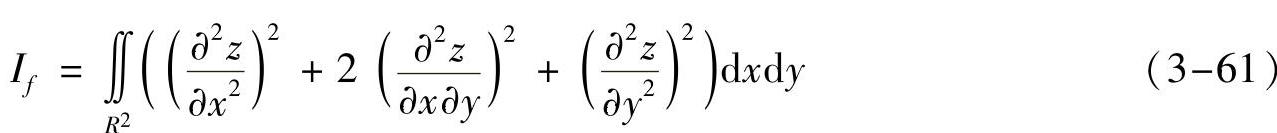
令P_i＝（x_i，y_i）（i＝1，2，...，n），定义三个矩阵。一个是n×n的矩阵K，公式如下：

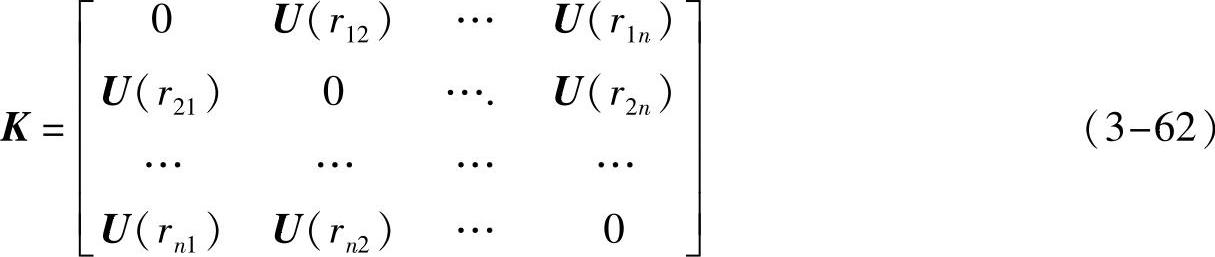
式中，r_i，_j为点P_i和P_j的欧氏距离。第二个是3×n的矩阵P，公式如下：

第三个是（n＋3）×（n＋3）的矩阵L，公式如下：

式中，“0”为3×3的零矩阵；P^T为P的转置。

要使金属板在点（x_i，y_i）的高度为z_i，需构建n维的行矢量V＝（z₁，z₂，...，z_n）和（n＋3）维的列矢量Y＝（V，0，0，0）。定义列向量W和系数a₁、a_x和a_y的公式如下：

L^-1Y＝（W a₁a_xa_y）^T（3-65）得到要求的函数如下：

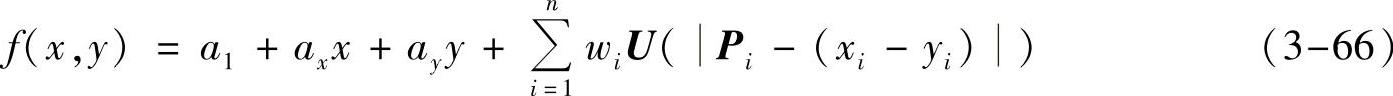
该函数满足三个约束条件：对于所有的i有f（x_i，y_i）＝z_i；函数f的积分I_f最小；I_f与WKW^T＝V（L^-1_akL^-1_a）V^T成正比。只有在W的所有分量都为0时积分值才为0，这时样条函数f（x，y）＝a₁＋a_ix＋a_iy。

薄板样条插值配准有效克服了通过ICP算法对特征点集进行配准时出现的奇异点现象，并且配准误差小，对应关系准确。TPS法的配准结果如图3-63所示。

（5）结果举例

两帧完成管腔轮廓提取的IVUS图像如图3-64所示，其中管腔轮廓上的钙化斑块区域段标注为黄色。根据二维特征描述算子对图像进行配准的结果如图3-65所示，可以看出，由于特定的距离和角度在不同的点对之间反复出现，因此造成匹配关系的紊乱。为了达到精确配准的目的，必须进一步丰富特征点的特征集，加强点特征的独特性和可识别性。

图3-63 TPS法的配准结果

a）点集的初始位置 b）配准结果

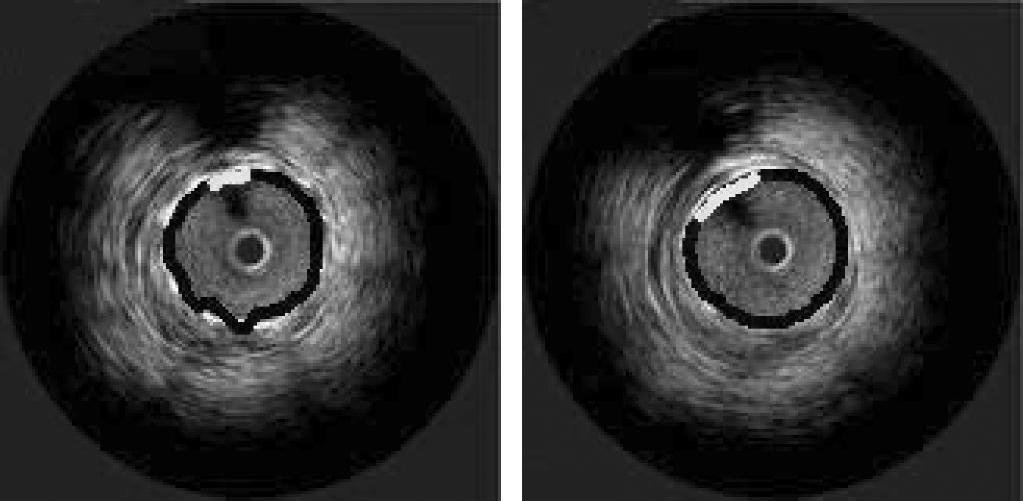
图3-64 两帧完成管腔轮廓提取的IVUS图像

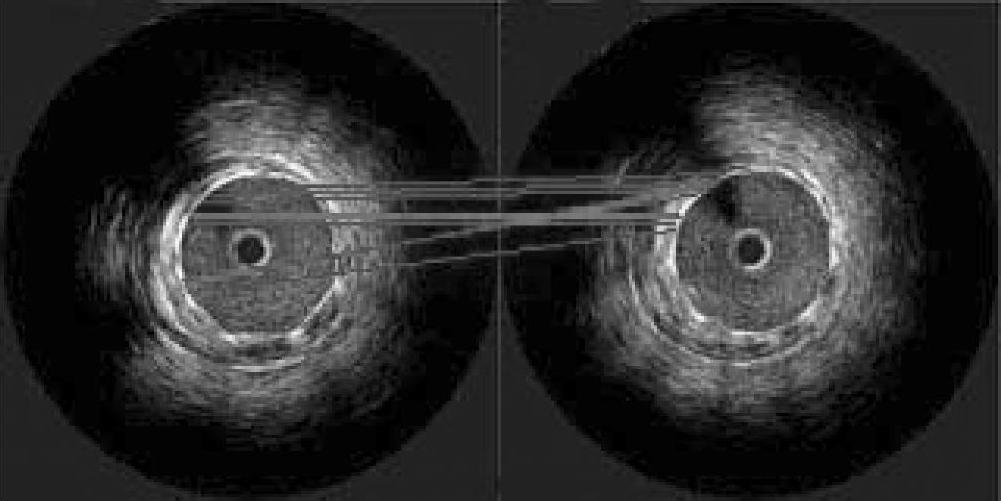
图3-65 二维特征描述算子对图像配准结果

IVUS图像的配准结果如图3-66所示，其中图3-66a是利用ICP算法进行配准的结果，可看出结果并不理想。图3-66b是将特征点的二维和一维算子融合在一起，根据综合特征采用TPS插值算法对图像进行配准的结果。通过比较两种方法的配准结果可得出以下结论：

1）ICP算法根据标志点之间的最近距离进行配准，忽略了特征点之间的一一对应关系，因此在图像形变较大的情况下配准效果不理想，容易出现一对多映射关系和奇异点现象。

2）ICP算法根据特征点的最近距离法则确定对应点之间的映射关系，且映射关系在0与1之间转换；而TPS插值算法通过扩散对应关系，使得特征点之间对应系数变为0～1之间的小数，使得对应关系变得更加平滑、连续，有效克服了对应关系的非1即0现象。

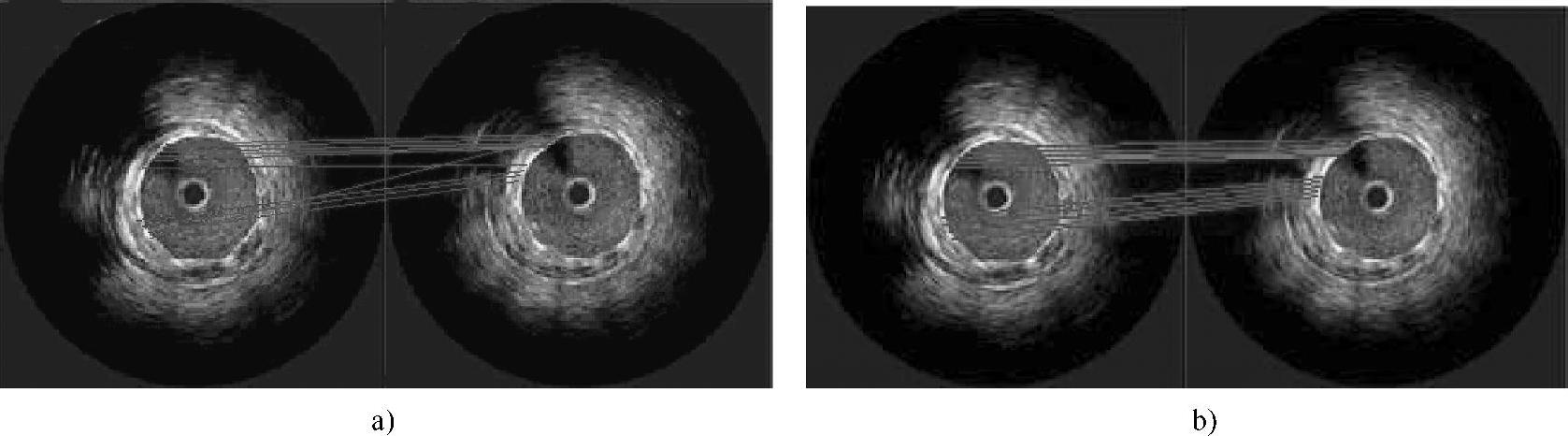
图3-66 IVUS图像的配准结果

a）ICP算法配准结果 b）TPS配准结果

3）在TPS插值算法的配准过程中，对每一次迭代后的特征点集进行插值，将映射分解为刚性映射和非刚性映射，通过最小化弯曲能量，联合点集之间的变换矩阵以及映射参数最终实现点集之间的弹性配准；而ICP算法配准过程中，每次迭代时单纯地依据最小距离法则对特征点进行插值变换，缺乏对特征点弹性变换的考虑。

4）TPS插值算法通过设置温度系数T控制对应关系，配准过程开始时T值较大，最小化能量公式中刚性映射部分比重较大，即配准过程更偏重于刚性映射；随着迭代过程的进行，T值逐渐缩小，能量公式中弹性映射的比重加大，使得配准更加富有弹性；还可以通过控制T的变化速率控制配准的步长，与迭代次数进行权衡，最终达到精确的配准结果。