基于Snake模型的三维分割方法优化

本节介绍一种基于snake模型的IVUS图像序列三维分割方法。在对原始图像进行滤波去噪和去除环晕伪像的预处理的前提下，首先获取IVUS序列的四个纵向视图，并从中提取出内腔和中-外膜边界；然后，将各纵向视图中的边界曲线映射到各IVUS帧中，得到各横向视图中的初始轮廓；将此初始轮廓作为snake模型的初始形状，通过使预先设定的能量函数最小，模型在内外力的共同作用下不断变形，最终得到各IVUS帧中的内腔边界和中-外膜边界，从而实现对各帧图像的并行分割。

基于snake模型的三维分割IVUS图像序列方法流程图如图3-23所示，该分割方法的步骤如下：

1）获取IVUS图像序列的四个纵向视图。

2）提取纵向视图中的内腔边界和中-外膜边界。

3）将步骤2中获得的边界曲线映射到各帧IVUS切片图像中，得到各IVUS帧的初始内腔边界和中-外膜边界。

4）在各IVUS帧中，初始轮廓演化变形，得到最终的内腔和中-外膜轮廓。

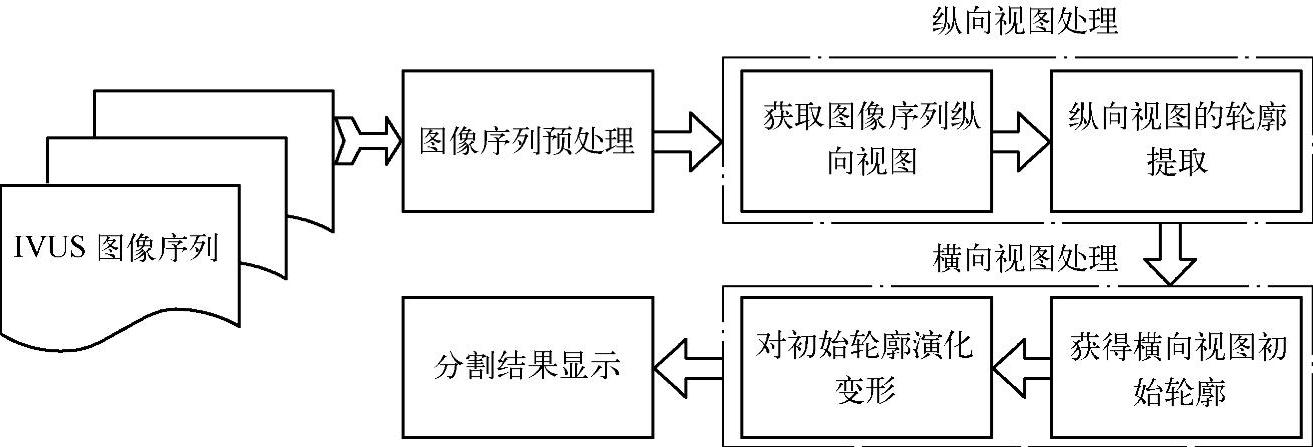
图3-23 基于snake模型的三维分割IVUS图像序列方法的流程图

（1）原始图像的预处理

首先，采用中值滤波和高斯平滑两种通用预处理方法，减少IVUS图像中的椒盐噪声和随机噪声。在IVUS成像过程中，超声导管在图像中心区域产生一个无回声暗区，围绕导管黑色影像的厚薄不一的白色环状影像称为环晕伪影（参见3.3.3节），即图3-24a中箭头所指部位。它与传感器声波振荡引起的高振幅信号有关，不是导管本身的影像，应该在预处理阶段加以去除，否则会影响图像分割的准确度。根据环晕伪影在IVUS极坐标视图中的分布特性，采用极坐标变换法对其加以去除。

图3-24 一帧IVUS图像的环晕伪影去除结果（ε＝0.21）

a） 原始横向视图 b）极坐标视图 c）去除环晕伪影后的极坐标视图 d）去除环晕伪影后的横向视图

其次，对IVUS横向视图进行极坐标变换，得到其极坐标视图，如图3-24b所示。可见，环晕伪影位于极坐标视图的上部。采用阈值法，按照下式去除极坐标视图中的环晕伪影：

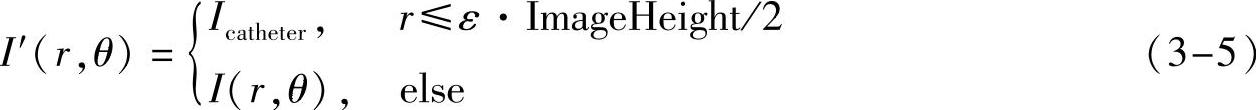
式中，I（r，θ）和I′（r，θ）分别为原极坐标视图和去除环晕伪影后的极坐标视图中像素点（r，θ）处的灰度值；I_catheter为原IVUS图像中导管区域的像素灰度值；r为像素点的极径；ε为权重参数，经实验确定其取值范围为［0.1，0.35］；ImageHeight为以像素为单位的图像高度。

去除环晕伪影后的极坐标视图如图3-24c所示，在极坐标视图中消除环晕伪影后，再经过极坐标逆变换，即可得到直角坐标系下去除环晕伪影后的横向视图，如图3-24d所示。对4帧IVUS图像去除环晕伪影的结果如图3-25所示。

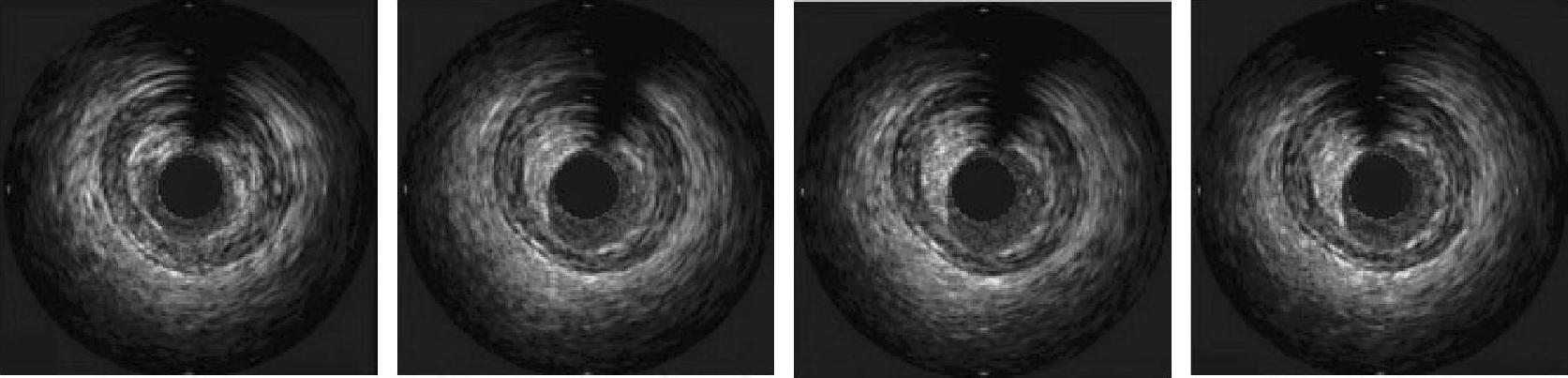
图3-25 去除环晕伪影的4帧IVUS图像

（2）获得IVUS图像序列的纵向视图

采集IVUS图像时，随着超声导管的缓慢回撤，获得的是一系列血管横截面切片图像。IVUS纵向视图是指IVUS图像序列沿平行于导管方向的纵向截面视图，如图3-26所示。沿血管长轴（纵向）方向取四个纵向视图，即垂直切面A、水平切面B、左对角线切面C和右对角线切面D。

（3）提取纵向视图中的血管壁边缘

IVUS纵向视图中的每一行像素即为一帧切片图像与该纵向视图的交线，其对应关系示意图如图3-27所示。根据纵向视图中的内腔边界和中-外膜边界的灰度同其周围像素灰度相差较大的特征，遍历纵向视图中的各像素，判断识别目标边界点。由于纵向视图中的目标边界分布于图像中部，所以从图像中轴线开始，分别向左和向右进行逐行遍历，如图3-28所示。对于当前像素（i，j），其灰度值为I（i，j），若I（i，j＋1）-I（i，j）≥η，η为阈值，则为目标边界点，否则不是。将每行左右两部分的像素中，第一个符合上述条件的像素记为内腔边界点，第二个记为中-外膜边界点。经实验确定η的取值区间为［10，20］。图3-29是对图3-25所示图像序列的四个纵向视图的血管壁边缘提取结果。

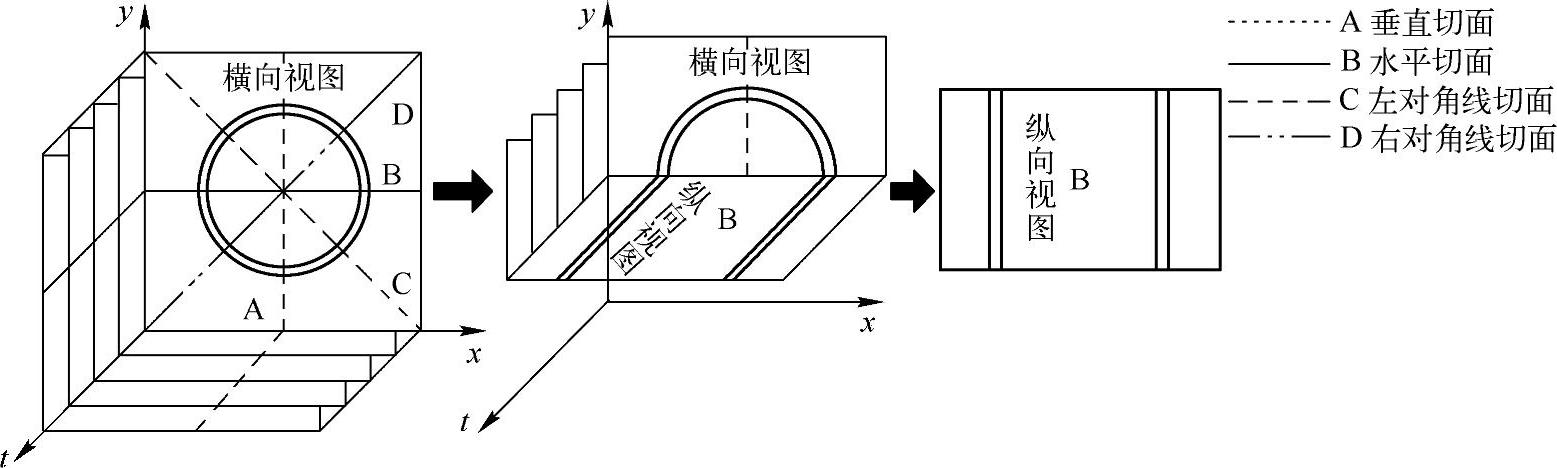
图3-26 获取IVUS纵向视图的示意图

图3-27 纵向与横向视图的对应关系示意图

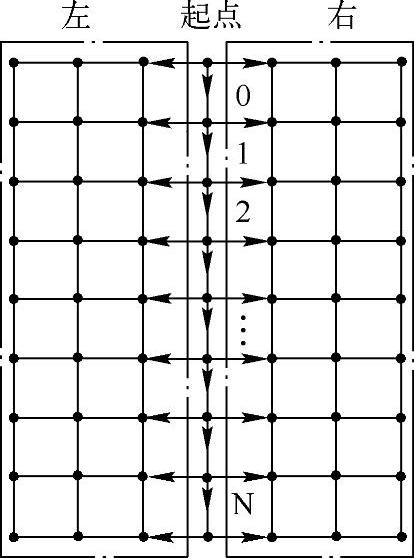
图3-28 逐行遍历纵向视图像素

(www.xing528.com)

图3-29 完成管腔轮廓提取的四个纵向视图

a） 垂直切面图 b）水平切面图 c）左对角线切面图 d）右对角线切面图

（4）获取横向视图中的初始轮廓

纵向视图的轮廓线对应到横向视图中为轮廓点，四条纵向视图轮廓线映射到横向视图中为四个轮廓点，如图3-30所示。在得到各帧横向视图中的内腔和中-外膜初始边界点以后，依次连接各初始边界点，获取初始轮廓，如图3-31所示，同时获得各帧图像中的初始内腔边界和中-外膜边界。图3-32是对图3-25所示图像序列的横向视图中初始轮廓的提取结果。

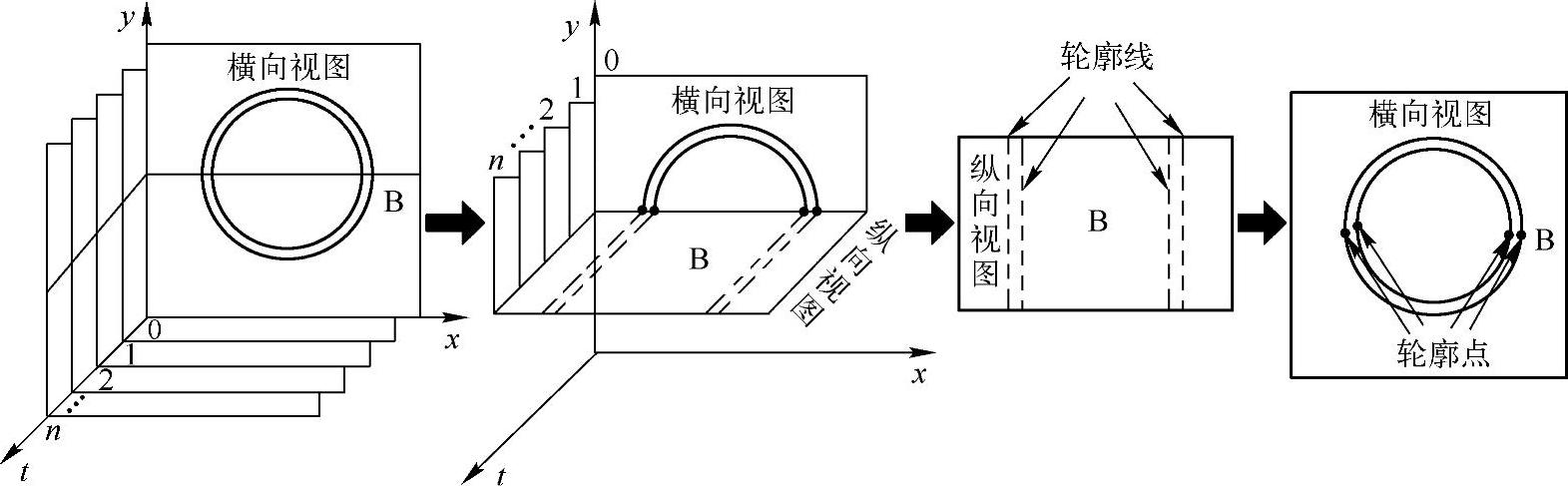
图3-30 纵向与横向视图轮廓对应关系示意图

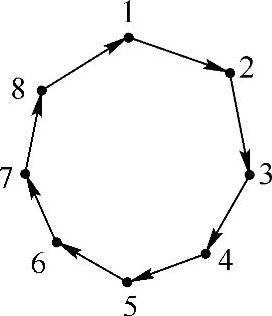
图3-31 由初始点获取初始轮廓

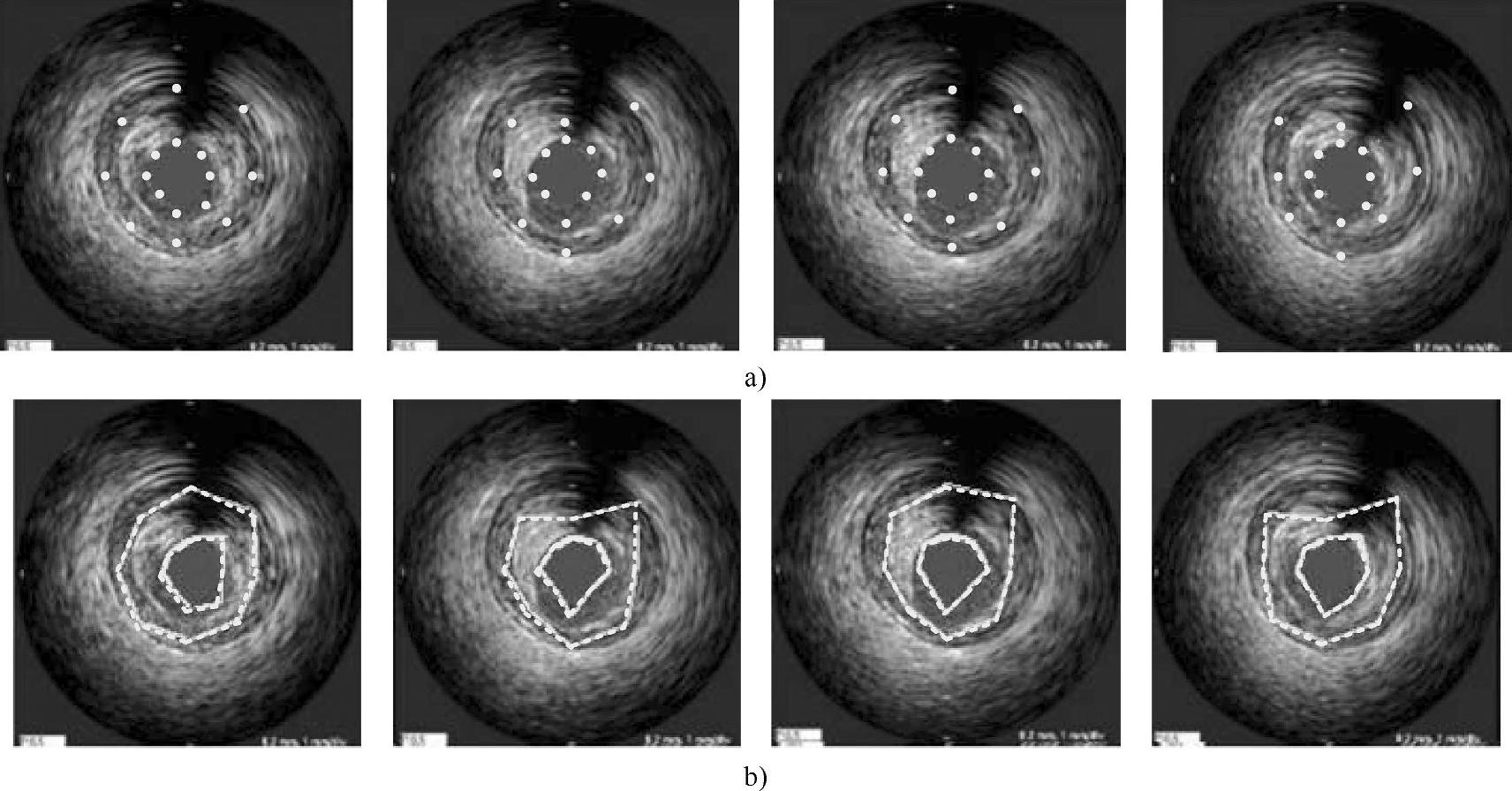
图3-32 IVUS横向视图中血管壁的初始轮廓

a） 初始轮廓点 b）初始轮廓

（5）基于snake的初始轮廓演化

将各帧IVUS图像中血管壁的初始轮廓作为snake模型的初始形状，通过使预先设定的能量函数最小，snake不断变形，当能量函数取得全局最小值时，snake模型即停留在目标轮廓处，从而完成对各帧图像中内腔和中-外膜边界的并行提取。

将初始轮廓离散成由N个点组成的有序点集，则snake能量函数的离散表达式为

式中，内部能量E_int使snake在变形过程中保持连续和平滑，其归一化表达式为

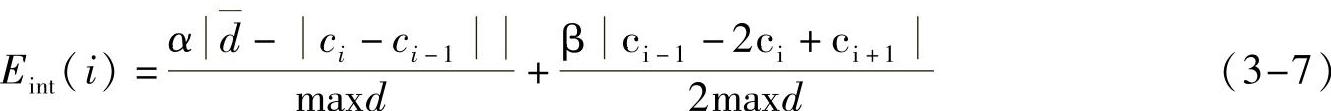
式中，c_i（x_i，y_i）（i＝1，2，…，N-2）是第i个snake点；d和maxd分别是相邻snake点之间的平均距离和最大距离，在每次迭代结束时，它们的值都被更新；α和β是权重参数。式（3-3）中的第一项保证变形过程中snake的连续性，使snake点均匀分布，不致产生收缩的现象；第二项是曲线二阶导数的离散形式，保证变形过程中snake的光滑性。由于进行了归一化，故式（3-7）中两项的取值范围都在［0，1］区间内，权重α和β的取值区间也是［0，1］。

外部能量E_ext是保证snake收敛的外部力，它决定snake的移动方向，其定义为

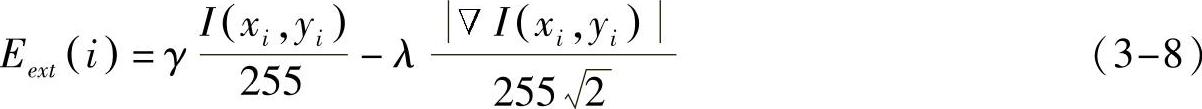
式中，I（x_i，y_i）和I（x_i，y_i）分别是像素（x_i，y_i）的灰度和灰度梯度值。由于8位灰度图像的灰度和灰度梯度的取值范围分别为［0，255］和［0，2552］，故对I（x_i，y_i）和I（x_i，y_i）分别进行归一化，使其取值范围为［0，1］。γ，λ∈［0，1］是权重参数。

通过使能量函数E最小，snake在内外力的共同作用下从初始形状开始不断变形，最终停留在能量函数取得全局最小值的最优位置，即为目标轮廓，如图3-33和图3-34所示，其中式（3-3）和式（3-4）中的权重参数设定为α＝β＝γ＝λ＝1，即各能量项的权重相等。

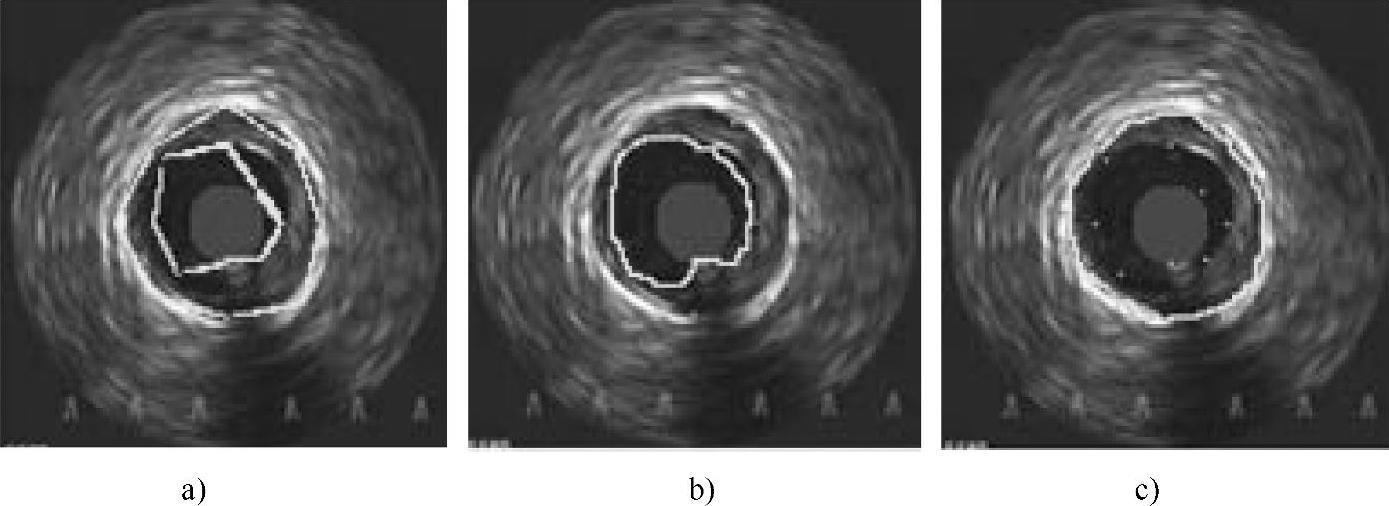
图3-33 轮廓演化结果1

a） 初始轮廓 b）内腔轮廓演化结果 c）中-外膜轮廓演化结果

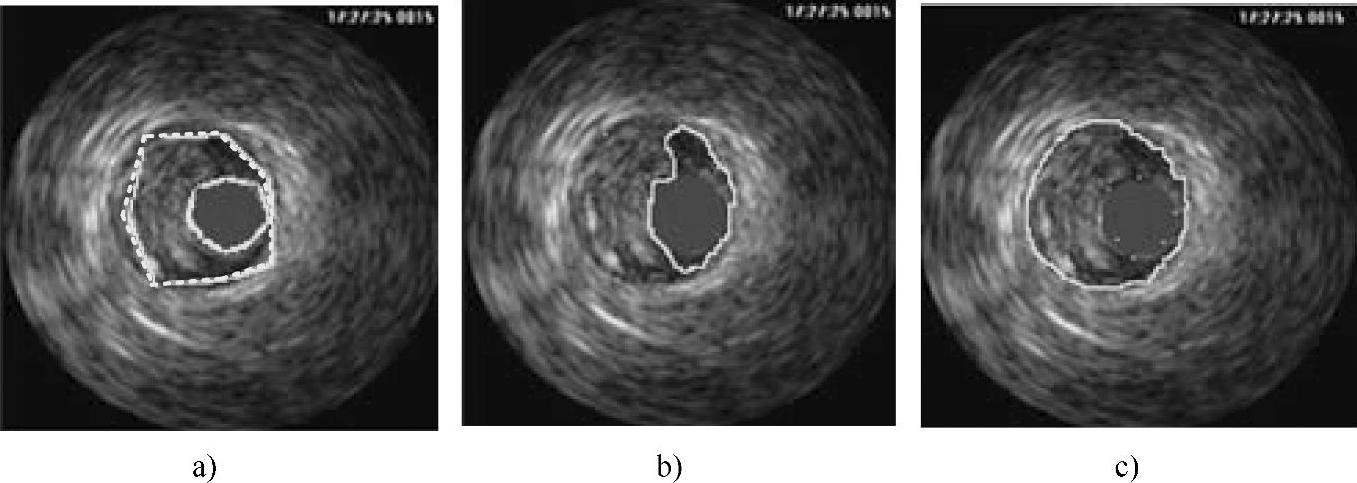
图3-34 轮廓演化结果2

a） 初始轮廓 b）内腔轮廓演化结果 c）中-外膜轮廓演化结果