近年来,基于偏微分方程的各向异性扩散方法已广泛应用于图像降噪、边缘检测、分割等领域的研究,它将异质扩散和迭代平滑的概念引入到图像处理中,在去除图像噪声的同时,保留甚至增强了图像中的边缘信息。
各向异性扩散方法的基本原理是利用梯度算子来辨别由噪声引起的图像梯度变化和由边缘引起的图像梯度变化,然后用邻域加权平均去除由噪声引起的小梯度变化,同时保留由边缘引起的大梯度变化,这个过程迭代进行,直至图像中的噪声被去除。
将原始图像f0(x,y)作为滤波器零时刻的输入f(x,y;0),t时刻滤波器对带噪图像f(x,y;t)的调整取决于前一时刻的输出,并满足以下偏微分方程[6]:
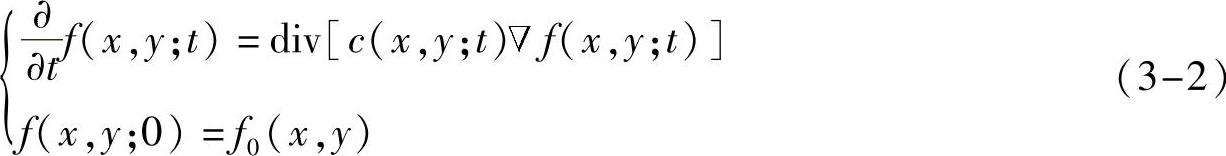
式中,div是散度算子;▽是梯度算子;c(x,y;t)是扩散系数。如式(3-2)所示,当前像素在t时刻的调整量取决于扩散系数c(x,y;t)和当前像素在邻域内梯度f(x,y;t)可被视为边缘强度的估计,而扩散系数的构造应该同时考虑边缘的强度和边缘幅值扩散门限。扩散系数构造可表示为如下扩散方程[6]:
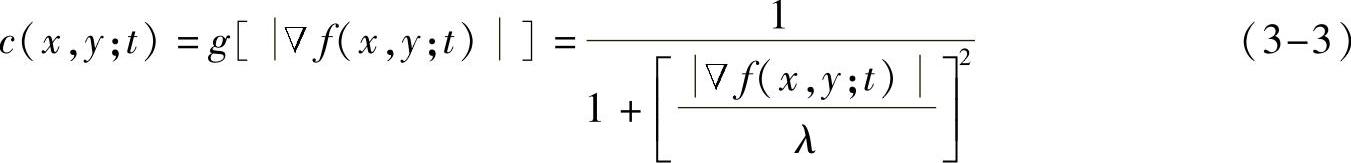
其中λ表示边缘幅值的门限参数。通过对上式的分析可知对于固定的λ,在同质区域内部,邻域内的梯度小,则扩散系数大,可以有效平滑同质区域内的噪声;而在图像的边缘部分,邻域内梯度较大,扩散系数小,则能够保留图像的边缘信息。
对于IVUS图像的各向异性扩散滤波包括以下步骤:首先,计算图像中每个像素点八邻域方向上的灰度梯度,即θ的值如图3-19b所示;然后根据式(3-3)计算每个像素点在对应的八邻域方向上的扩散系数cθ;最后,求得图像在该方向上的滤波后图像,经过迭代得到最后的结果图像。
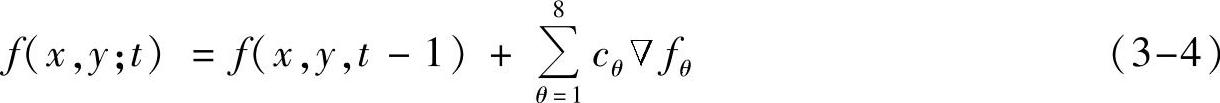
 (https://www.xing528.com)
(https://www.xing528.com)
图3-19 像素点的邻域表示
a)八连通邻域 b)梯度计算
对临床IVUS图像的实验结果如图3-20所示。考虑改变各向异性扩散边缘幅值的门限参数λ与迭代次数n,对图像的平滑滤波结果所造成的影响。其中图3-20b~图3-20d是各向异性扩散滤波的边缘幅值的门限参数λ分别设为10、5、15时的结果,可以看出,边缘幅值的门限参数越大,则可以突出的边缘特征越少,滤波后的结果图像越模糊。图3-20e、图3-20b和图3-20f是各向异性扩散滤波迭代次数n分别为50、100、150时的结果,可见随着迭代次数的增多,图像中边缘轮廓以外的区域越模糊。

图3-20 对临床IVUS图像的实验结果
a)原始图像 b)n=100,λ=10 c)n=100,λ=5
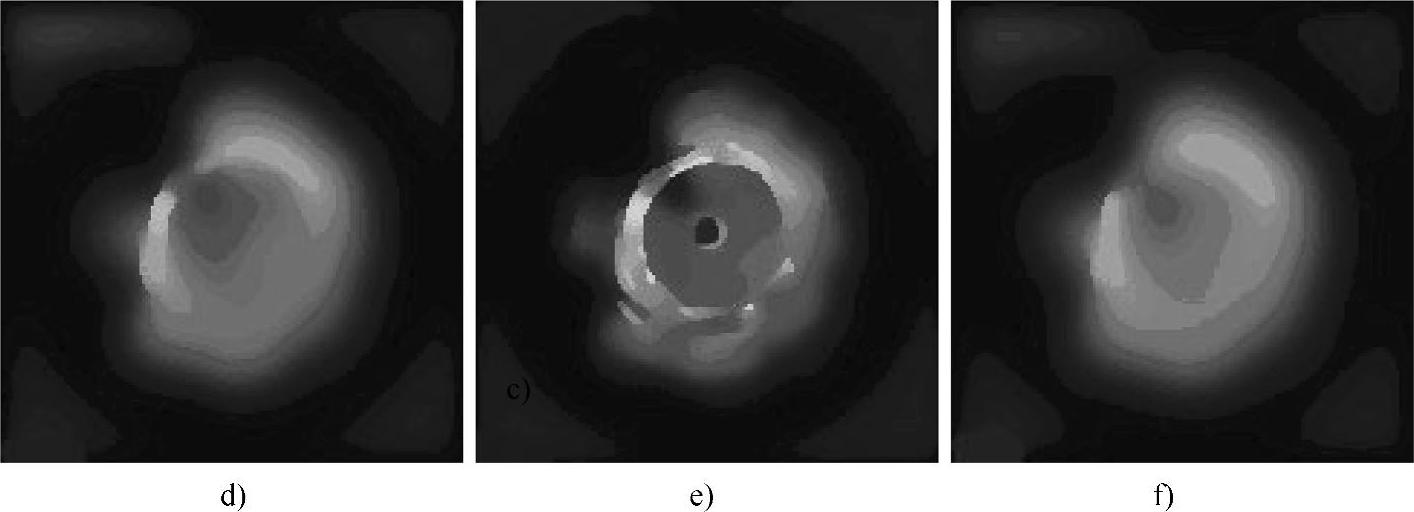
图3-20 对临床IVUS图像的实验结果(续)
d) n=100,λ=15 e)n=50,λ=10 f)n=150,λ=10
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




