CAG图像序列的三维运动跟踪优化方案

为了实现对冠脉在整个心动周期中的四维（三维＋时间）描述，现有的方法多是按照“自底向上”，即二维→三维的顺序，逐个时刻进行血管骨架的三维重建。具体方法是首先从同时拍摄的两个角度的图像中提取出主要血管分支的中心线（骨架），之后进行左右两个角度间骨架对应点的匹配，最后根据两个投影点的坐标，计算出空间点的三维坐标。由于需要首先从原始图像中提取出单像素、八连通的血管中心线，因此结果的精度在很大程度上取决于二维提取的准确度。而临床得到的造影图像通常受噪声污染严重，而且图像中经常会出现血管重叠，这种情况下仅从一个角度的图像很难得到准确的血管轮廓。同时两个角度之间的匹配直接影响到重建的精度。对于离散的二维中心线，一般是利用外极线约束逐点匹配，该方法很难达到较高的精度，重建结果的连续性不好，计算量也很大。

采用snake模型，按照“自顶向下”的方式，将前一时刻的血管骨架作为当前时刻snake模型的初始位置，通过使适当的能量函数最小化，表示血管骨架的曲线直接在三维空间中变形，可完成血管骨架的三维序列重建。三维血管骨架在成像平面上的投影就是二维血管中心线，因此该方法可将序列图像中血管的二维中心线提取、三维重建和相邻时刻间的三维运动跟踪集成到一个框架中完成，实现对动脉血管在整个心动周期中的四维（三维＋时间）描述。采用连续的曲线（如B样条曲线）表示血管骨架，通过调整控制点的位置就可以灵活控制曲线的位置。同时在三维重建的过程中，避免了两个角度间的逐点匹配过程，通过使snake曲线变形，求解最优化问题，直接获得血管段的三维坐标，可提高三维重建的精度。算法的流程如图2-88所示，主要步骤包括：

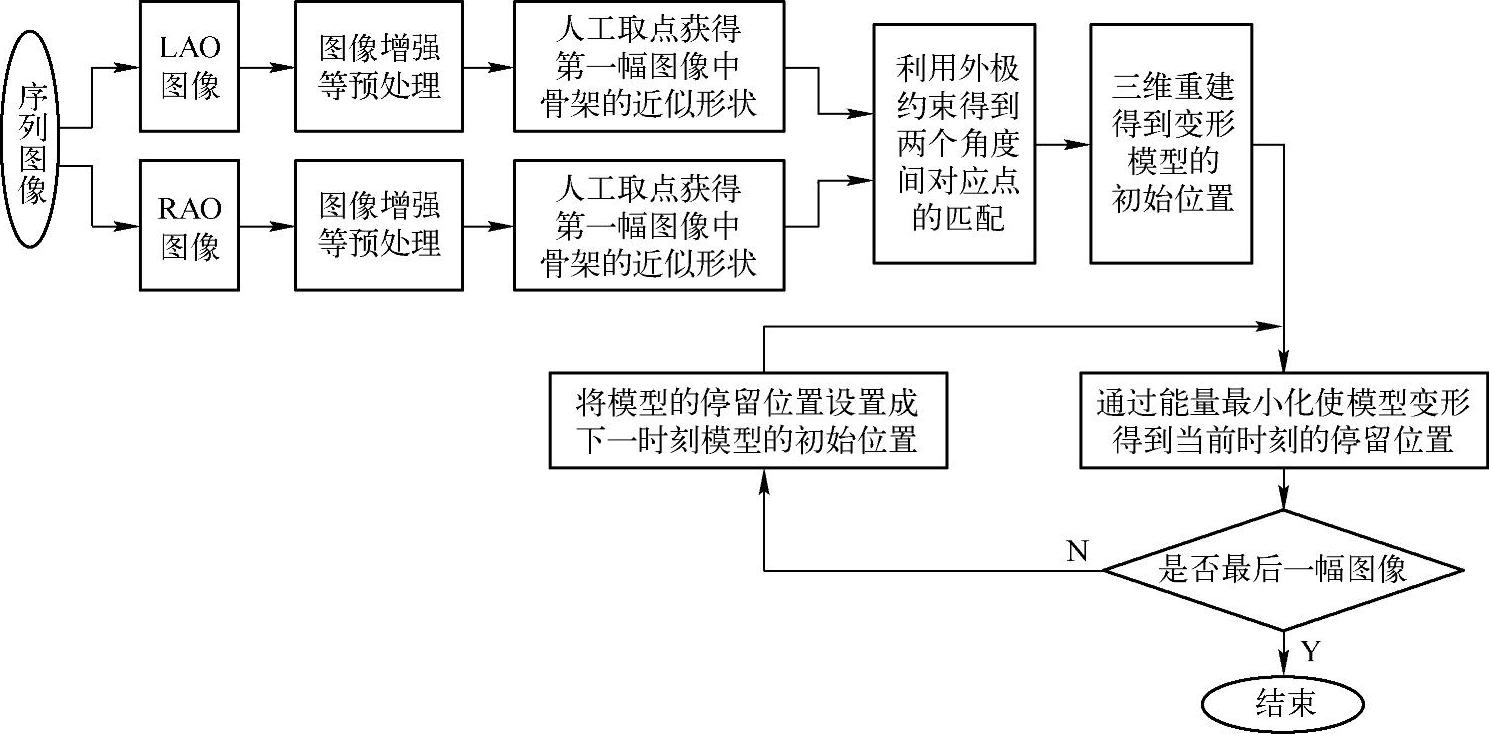
图2-88 基于变形模型的血管三维运动跟踪算法流程图

1）对原始图像进行必要的预处理，主要包括均衡对比度、去除噪声和图像增强等。

2）对于第一时刻的图像，通过人工取点获得感兴趣血管段在左右投影中的近似中心线，用折线表示。

3）对手动获取的采样点进行三维重建，连接各三维点，所得折线作为snake的初始位置。

4）通过使预先设定的能量函数最小，snake在空间中变形，最终得到具有最小能量的最优位置，就是第一时刻的三维血管中心线。

5）以前一时刻的三维血管骨架作为当前时刻snake的初始位置，完成整个序列中骨架的跟踪和重建。

（1）第一时刻血管骨架的三维重建

首先得到第一个时刻血管段的三维中心线，对于其后的序列图像，可将前一时刻的骨架作为snake模型的初始位置，通过模型变形得到当前时刻的三维骨架。

对于序列中的第一幅图像（包括左右两个角度），通过人工取点获得兴趣血管段在两个角度投影中的中心线的近似形状，采用外极线约束获得两个角度的采样点间的匹配关系，并计算出采样点的三维坐标，作为变形模型控制点的初始位置。使能量函数最小，模型在三维空间中变形，最终停留在总能量最小的位置，就是该时刻血管段的三维中心线，结果是用三次B样条曲线表示的一条连续曲线。

在跟踪过程开始前，需要已知变形模型的初始位置，可通过人工取点提取近似的血管中心线。方法是首先从一个角度的图像中手动选取感兴趣血管段上的n个控制点（n的大小视情况而定），然后根据外极线约束得到各点在另一个角度图像上的对应点，最后由两个角度的点对，计算出各控制点的三维坐标。

三维重建的关键问题是如何确定两个角度造影图像上点的对应关系。寻找三维空间中的骨架点在两个不同角度造影成像面上的对应投影点的过程称为立体匹配。对两个成像面上的点进行立体匹配时，首先在其中一个投影面上取二维投影点p，如图2-30所示，通过点p、S₁和S₂确定外极面，然后确定外极面与另一投影成像面的交线（即外极线），最后在该外极线上寻找血管骨架点与点p相匹配。由于二维处理的误差、几何变换矩阵的误差等，匹配点可能不会准确地出现在图像平面中对应的外极线上，而在外极线的邻域内。一般在该邻域内搜索和外极线距离最短的点作为匹配点。由这些对应点分别求出它们的三维坐标，用直线连接这些三维点，所得的折线作为三维变形模型的初始位置，如图2-89所示。外极线和三维点坐标的计算方法详见第2.5节。

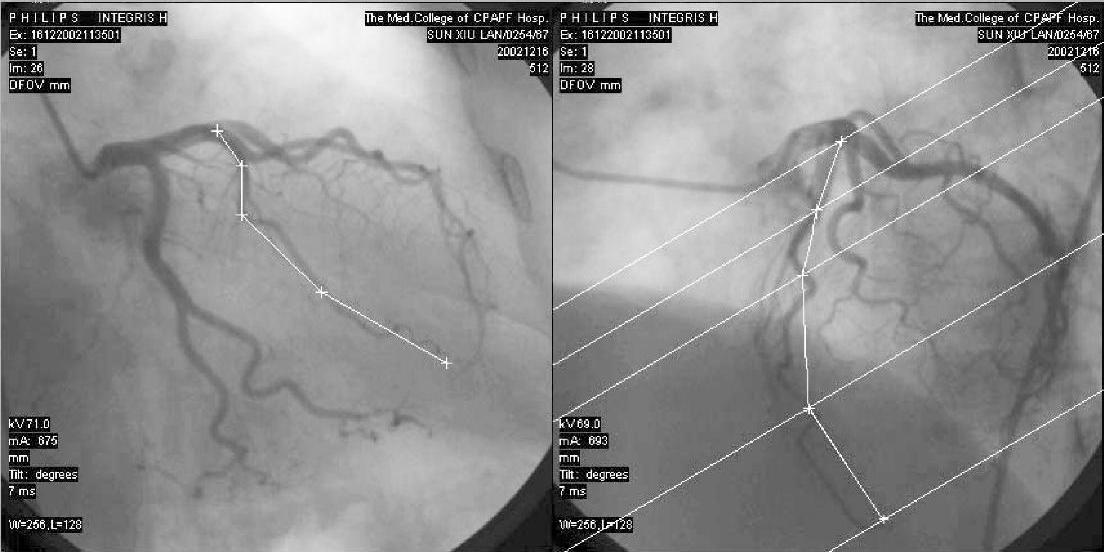
图2-89 第一时刻两个角度图像中采样点的外极线匹配结果

snake是一条可变形的参数曲线，c^→（s）＝（x（s），y（s），z（s）），s∈［0，1］。将该曲线离散化为n个点c^→_i（x_i，y_i，z_i）（i＝1，2，…，n），那么snake模型能量函数的离散形式如下：

内部能量E_int的表达式如下

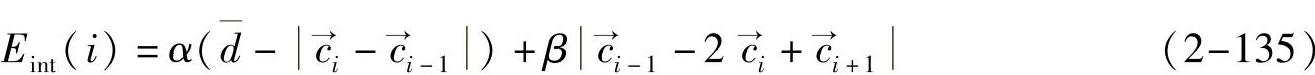
式中的第一项约束使点平均分布，既能满足连续性的要求，又不会产生曲线收缩的现象。在每次迭代结束时，点间的平均距离 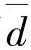的值被更新；第二项是曲率，使曲线保持平滑。α和β是权值。

造影过程中，当造影剂的浓度达到峰值时，所拍摄的图像上血管的灰度值应比背景的灰度值小，所以外部能量应该吸引表示血管骨架的空间曲线移动到如下位置：三维曲线在两个图像平面和上的投影位于图像上灰度最小、且灰度梯度最小的区域，即血管的2D中心线。根据透视投影成像的几何关系和外极线约束关系可知，空间点在两个成像平面上的2D投影点的坐标都是空间点三维坐标的函数。下面具体介绍其推导过程。

如图2-27所示，设冠脉骨架点P_i在坐标系x₁y₁z₁s₁和x₂y₂z₂s₂中的坐标分别为（x₁i，y₁i，z₁i）和（x₂i，y₂i，z₂i），P_i在图像A和图像B上的投影点坐标分别为（u₁i，v₁i）和（u₂i，v₂i）。根据透视投影成像的几何关系可得出如下公式：

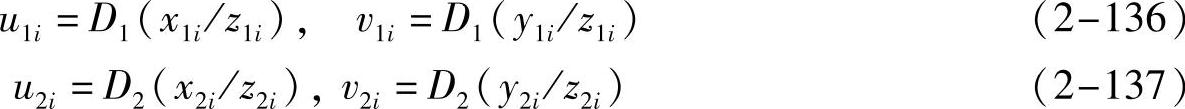
两个角度的X射线源局部坐标之间的变换关系为：

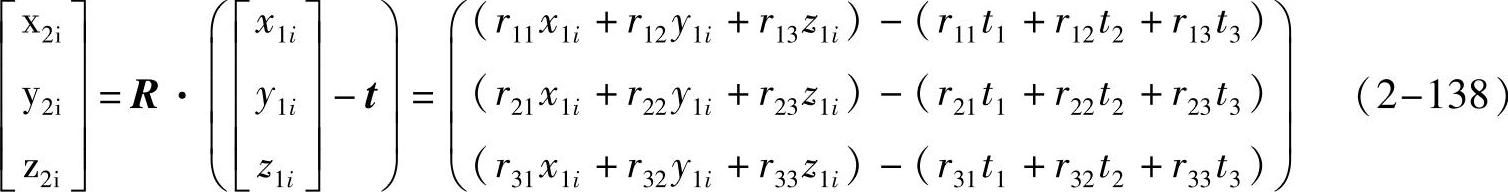
式中，r_ij（i，j＝1，2，3）为旋转矩阵R的第i行、第j列的元素；t＝［t₁t₂t₃］^T

为平移矩阵。将式（2-138）代入式（2-137）得到如下公式：

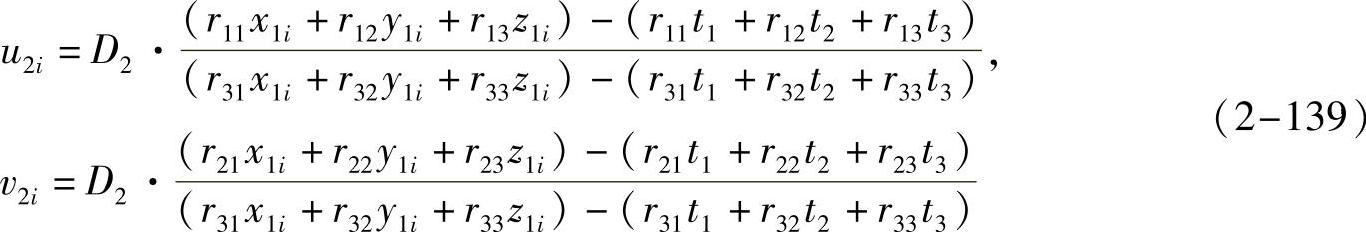
所以空间点在两个成像平面上的二维投影点的坐标（u₁i，v₁i）和（u₂i，v₂i）都可以用该点的三维坐标 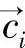＝（x₁i，y₁i，z₁i）来表示，公式如下：

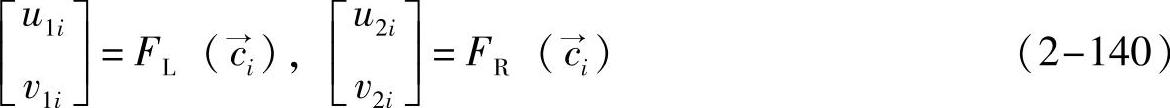(www.xing528.com)

外部能量函数包含两部分，分别对应于两个角度的二维投影，公式如下：

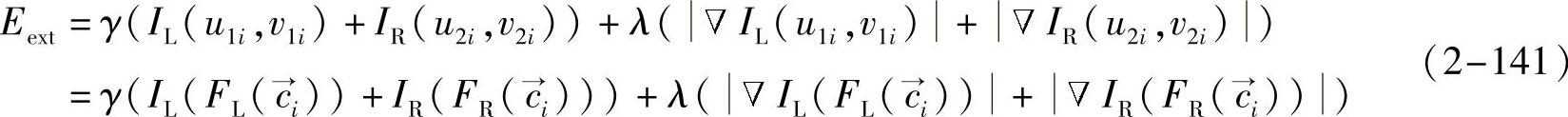
式中，I_L（u_1i，v_1i）和I_R（u_2i，v_2i）分别是左、右图像点的灰度值；I_L（u_1i，v_1i）和I_R（u_2i，v_2i）分别是左、右图像点的灰度梯度。由于血管造影图像中，血管的灰度值比背景小，所以这里系数γ取正值。而且我们感兴趣的是血管中心线，不是边缘，所以λ也取正值。

求解变形模型的最优位置就是要使E最小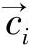， 的最终位置就确定了感兴趣血管段的三维中心线。求解能量函数最小化方程可采用动态规划或贪婪算法求解。

（2）整个序列中三维血管中心线的跟踪

得到第一时刻血管段的三维中心线之后，对于其后的序列图像，根据血管形状不突变的特点，把时刻t的三维骨架作为时刻t＋1模型的初始位置，实现对整个图像序列中血管段的三维运动跟踪。

在进行相邻时刻间的血管跟踪时，如果使模型不断变形的外力仅仅是图像点的灰度和相邻点间的灰度梯度，那么由于兴趣血管段不一定是二维投影中灰度最小、灰度梯度变化最小的部分，因此很容易收敛于错误的结果。基于上述原因，为了得到对序列图像中血管段的准确跟踪，需要引入其他的外部约束。考虑到外部能量函数的灵活性，可在模型中嵌入相似度匹配，通过对相邻帧之间的目标进行配准实现对运动物体的跟踪。假设在足够短的时间间隔内，运动前后物体的灰度不发生变化，那么得到序列中第一时刻的血管中心线之后，在开始对后续图像进行运动跟踪时，外部能量的函数表达式采用如下形式：

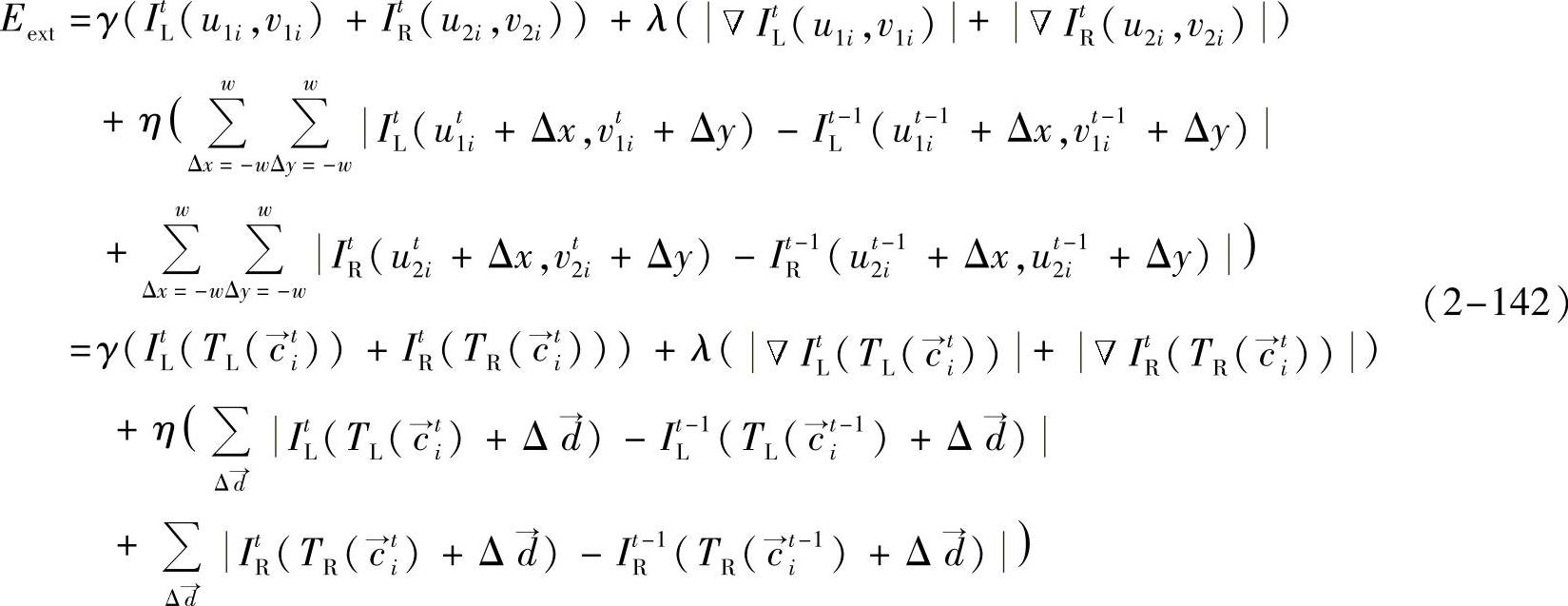
其中下标L表示LAO投影，R表示RAO投影。这样外部能量中除了包含图像力，即吸引曲线向着图像中灰度最小、灰度梯度变化最小的区域内移动之外，还包含外部约束，使运动前后血管上对应点的灰度变化最小。

同时引入一个新的运动模型，包含血管的整体运动和局部运动。假设在t-1时刻的3D血管中心线用曲线v^→_t-1（s）＝（x_t-1（s），y_t-1（s），z_t-1（s））表示，若相邻帧之间血管不发生严重的变形，那么下一时刻t的血管3D骨架v^→_t（s）与上一帧图像之间的运动可以分解为整体运动和局部运动，由于心脏及其相关的冠状动脉血管的运动是非刚性运动，因此整体运动包含整体平移、旋转和变形，那么 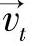（s）可用下式表达：

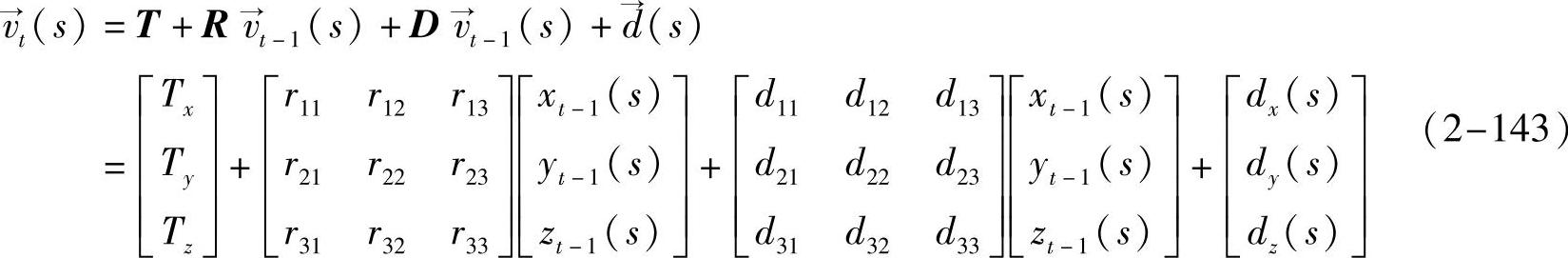
这样，血管在上一帧图像中的位置就不仅仅是它在下一帧图像中的位置的初始值了，同时它也是新位置的一个组成部分。式中，T是整体平移向量；R是整体旋转矩阵；D是变形矩阵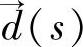； 是血管上每个点的局部位移。将上式中的前三项合并，得到如下公式：

其中，A是一个3×4的矩阵，

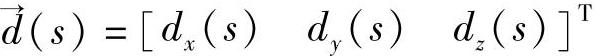
，对于每个点来说是一个3×1的列向量，表示该点的局部位移。

能量函数中的内部能量是为了保证曲线的连续性和光滑性，在进行运动分析时，可用该光滑性约束来对血管的运动速度进行约束。基于此，引入整体运动模型，血管的运动可以看做包含两部分：一个是整体运动，它与血管在上一帧的位置有关；另一部分是局部运动。重新构造能量函数如下：

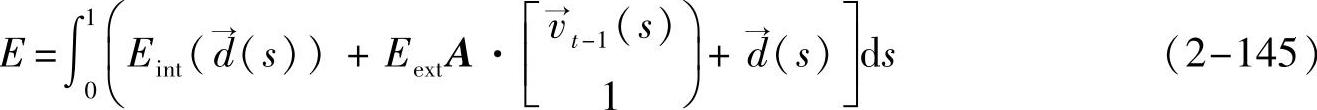
式中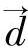， d（s）是血管上的点从上一帧到下一帧的局部位移（包括x和y方向的位移）；v^→_t-1（s）是血管点在上一帧图像中的位置（坐标）。上述能量函数的离散形式如下：

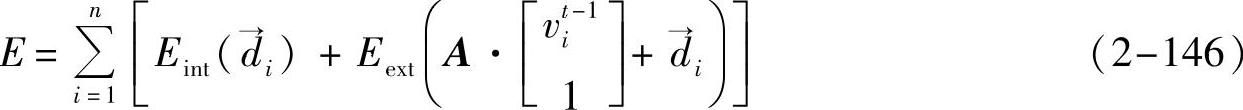
这样对血管的运动进行跟踪的问题就转化为求解矩阵A和d_i。

采用动态规划或者Williams快速算法求解snake能量函数最优化问题时，每次迭代时，需在以当前点为中心的一个小体元内进行搜索，算法示意图如图2-90所示。

选择分别从RAO30°CAUD24°角度和LAO46°CRAN21°角度拍摄的两个左冠造影图像序列，图像采集速率为15f／s，图像大小为512×512像素，灰阶为256。图2-91a是该序列中

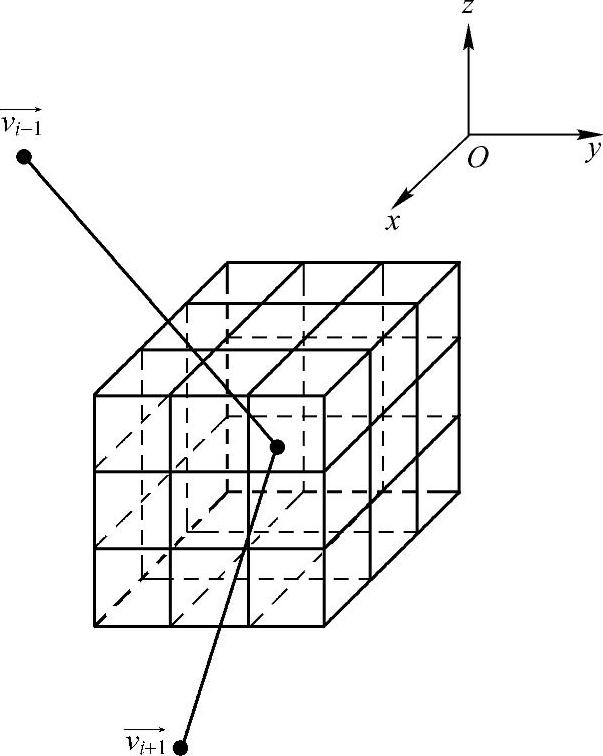
图2-90 求解3Dsnake模型最优化 问题的快速算法示意图

第一个时刻的两个角度的图像对，在RAO图像的前降支上选择8个点，根据外极约束可找到其在LAO图像中的匹配点。根据这些点的两个二维投影可以计算出它们的三维坐标。用直线段连接这些3D点，得到用折线表示的3D骨架的初始形状。在折线上均匀采点，通过使能量函数（式（2-141））最小，得到第一时刻的3D血管骨架，它在两个成像平面上的投影就是前两幅图像中的二维骨架，如图2-91b所示。对于其后的序列图像，根据血管形状不突变的特点，把当前中帧图像中snake模型的停留位置作为前一帧图像中的初始位置，实现序列图像中血管中心线的三维重建和跟踪，图2-92是从序列中选取的5个时刻的三维血管骨架跟踪结果。直观判断，三维血管骨架与原投影图像吻合很好。而且当一个心动周期结束时，即第10时刻的血管形状与第1时刻的形状很相似，这也验证了“在心动周期结束时，冠状动脉血管会回到其在周期开始时的位置”这一结论。

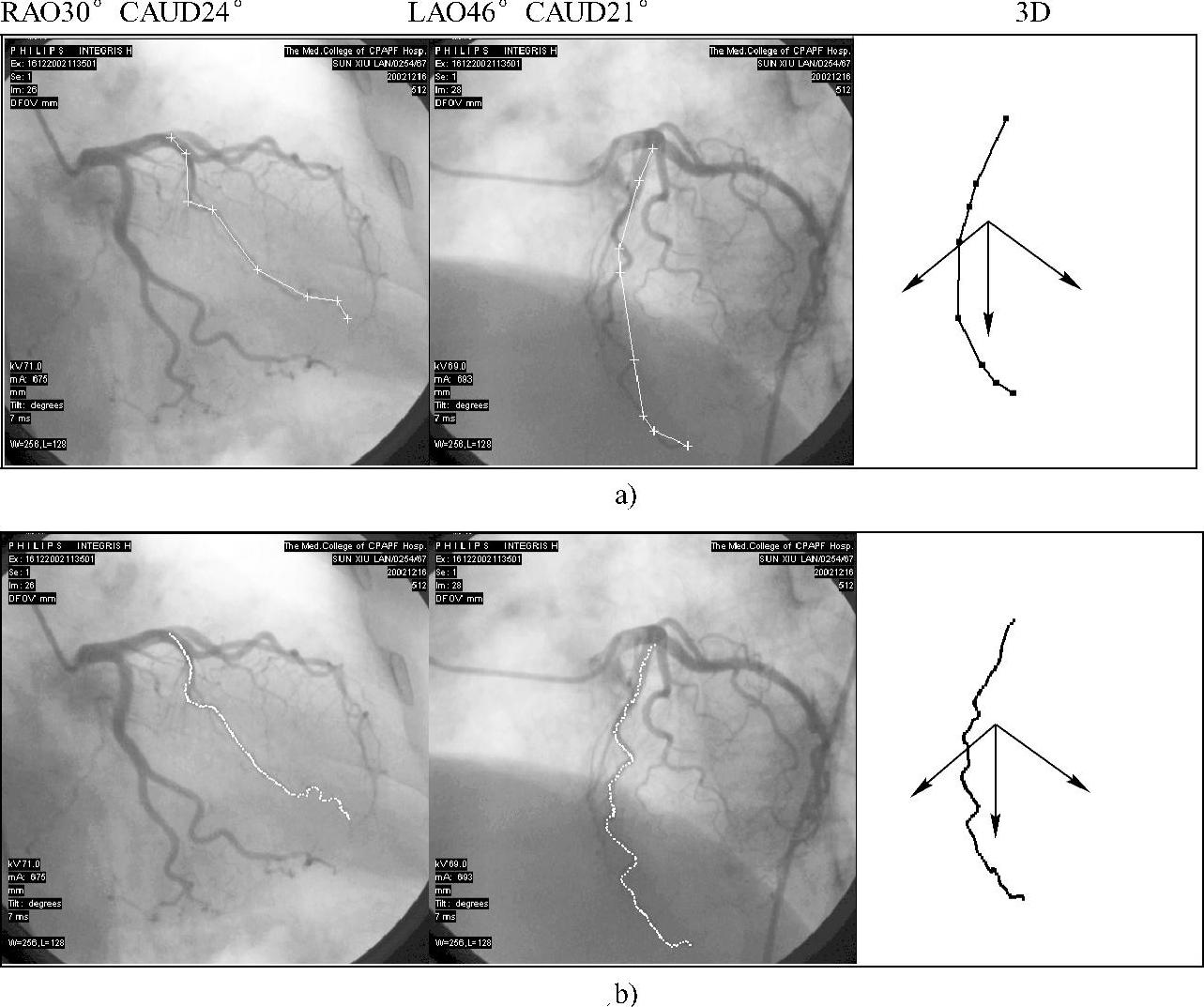
图2-91 序列中第一个时刻的左前降支中心线的三维重建

a）snake模型的初始形状 b）snake模型的最终停留位置