基于弹性配准的运动估计优化方案

该方法的基本思想是将血管骨架的运动估算转化为对连续两帧图像中同一段血管的骨架进行匹配，选择适当的匹配误差函数（即运动前后物体的差异度），通过使其最小，得到两帧图像之间骨架点的对应关系，那么以对应点作为两个端点的向量就是运动向量。

假设已经从CAG图像序列中提取出了各时刻主要血管分支的单像素、8连通的中心线（即骨架）。分别将两帧图像中某一血管分支的中心线表示为包含M个和N个像素的有序序列s₁和s₂，其中s₁（m）＝［x₁（m），y₁（m）］（m＝0，1，…，M-1）是骨架s₁中的第m个像素，为了简单起见，用s^m表示；s₂（n）＝［x₂（n），y₂（n）］（n＝0，1，…，N-1）是骨架s₂中的第n个像素，用sⁿ2表示。由于心脏会发生膨胀或收缩变形，因此M与N不一定相等，这里设N≥M。用对应关系或运动向量表示像素的位置从这一帧到下一帧的变化，如图2-83所示，s^m₁与sⁿ₂之间的运动向量为

d（m，n）＝s₂（m）-s₁（n）＝（x₂（n）-x₁（m），y₂（n）-y₁（m）） （2-129）

考虑到运动场的光滑性和血管的形状相似度，同时由于变形前后血管的长度可能不同，因而需考虑对无匹配部分的处理，以保证匹配的均匀性，设计如下的匹配误差函数：

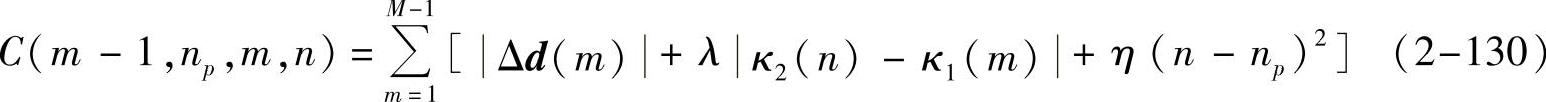
式中，n是s₂中与s^m₁相匹配的点的序号；n_p是s₂中与s^m-1₁相匹配的点的序号；Δd（m）＝d（m，n）-d（m-1，n_p）为相邻点的运动向量之差，如图2-83所示；λ和η是权重参数；κ_i（x）是曲线i在点x处的曲率，其近似计算方法如下：

式中，θ₁（m）是向量s₁（m）-s₁（m-1）和向量s₁（m＋1）-s₁（m）的夹角，如图2-84所示。

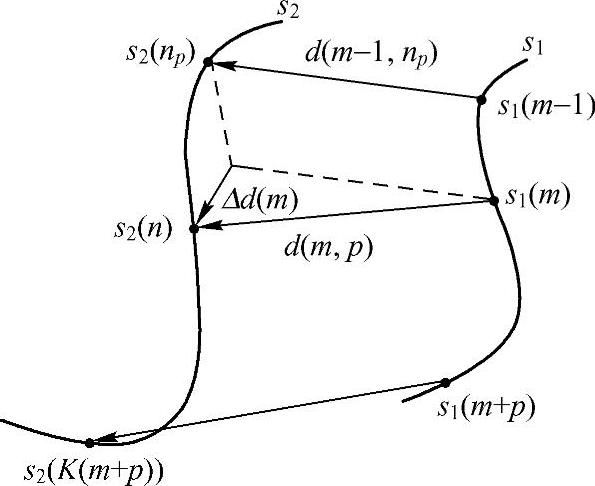
图2-83 变形前后的血管骨架点的对应关系

图2-84 曲线上相邻两点的向量夹角

式（2-130）中的第一部分是s₁中相邻点的运动向量变化（包括大小和方向的改变）。考虑到同一物体上物理相连的两点的运动是相似的，因此为了保证运动场的光滑性，应使s₁中相邻点的运动向量变化最小。第二部分是变形前后的血管骨架上对应点的曲率变化，它表达了血管形状的改变。由于心脏的膨胀和收缩，通常情况下N≠M，若设N＞M，那么s₂中就有一部分点无匹配。式（2-130）中的第三部分η（n-n_p）²是为了保证相邻的匹配像素之间不会有大的跳跃，使无匹配的部分尽量小，从而得到均匀的匹配结果。

通过使匹配误差函数最小，从s₂中找出M个点，这些点是s₁中相应的M个点（s⁰₁，s¹₁，…，s^M-1₁）的最优匹配。采用动态规划（Dynamic Programming，DP）完成对最优匹配的搜索，可大大减少计算量，节省计算时间，而且非常适合于编程。动态规划是运筹学的一个分支，是求解决策过程最优化的数学方法，其实质是分治思想和解决冗余。基本思想是在最优化的假设前提下，把一个N个变量的问题分解成N个阶段单变量的问题加以解决。动态规划示意图如图2-85所示，图中s₁s₂平面中的每个栅格点都表示一个数对［s₁（m），s₂（n）］，它是两幅图像中元素的一个可能的组合。两幅图像一个完整的配准可以看做是连接第一幅图像的元素与它在第二幅图像上的匹配元素的组合的一条路径。DP的目的就是找到最佳路径，即使得m＝M时各数对的累计成本最小的路径，具体步骤为开始时，m＝1，根据已知的成本函数计算出每个可能数对［s₁（1），s₂（n）］，n＝1，2，…，N的成本值。在接下来的步骤m（m≥2）中，确定终点为［s₁（m），s₂（n）］，n＝1，2，…，N的具有最小累计成本值的路径（最佳路径）。方法是连接该点与前一步中的各点［s₁（m-1），s₂（1）］（l＝1，2，…，N），计算出各条路径的成本值，并且从中选择出具有最小累计成本值的路径。令c（m，n，m-1，u（m-1））为连接点［s₁（m），s₂（n）］和上一步中的点［s₁（m-1），s₂（u（m-1））］的成本值，C（m，n）是终点为［s₁（m），s₂（n）］的路径的最小累计成本值。将成本值加在C（m-1，u（m-1））上，得到累计成本值Q（m，n，m-1，u（m-1））。对于步骤m中的每个节点［s₁（m），s₂（n）］，有N个累计成本值Q（m，n，m-1，u（m-1）），u（m-1）＝1，2，…，N。C（m，n）由下式定义：

图2-85 动态规划示意图

(www.xing528.com)

如前所述，有下式：

c（m，n，m-1，u（m-1））＝Δd（m）＋λκ₂（n）-κ₁（m）＋η［n-u（m-1）］² （2133）

且C（0，0）＝0。产生最小累计成本C（m，n）的节点［s₁（m-1），s₂（u（m-1））］就成为节点［s₁（m），s₂（n）］的先趋。对于所有的M个像素重复上述过程，在最后一步即m＝M时得到的最佳路径也就是整个问题的最优路径。

最后，令｛s₂（u_n（m-1）），s₂（u_n（m-2）），…，s₂（u_n（1））｝为与终点［s₁（m），s₂（n）］的路径相关的像素，这样属于路径n的全部节点就是｛［s₁（1），s₂（u_n（1））］，［s₁（2），s₂（u_n（2））］，…，［s₁（m），s₂（n）］｝。在每个节点［s₁（m），s₂（n）］处，都需要计算连接该点与前一步的每个点［s₁（m-1），s₂（k）］（k＝1，2，…，N）的成本值，因此DP的复杂度为O（MN²）。

为了避免逐个像素进行比较，减少计算量，缩短计算时间，考虑到冠脉血管运动的实际情况，可以附加一些约束条件限制可能解的搜索空间，具体条件如下：

1）唯一性约束：对于s₁中的每个像素，在s₂中都能找到一个元素与之相匹配，即∀m，∃ns₁（m）→s₂（n），该约束保证只考虑s₁中各元素的最佳匹配。

2）单调性约束：因为大多数的心脏变形并不改变冠脉血管骨架上元素的顺序，因而在匹配的过程中需保证骨架线上像素点的顺序不变，不允许交叉匹配，即如果s₁（m）→s₂（n）且s₁（m-1）→s₂（n_p），那么n≥m且n＞n_p，该约束避免了“多对一”（即s₁中的多个元素与s₂中的一个元素相匹配）以及交叉匹配。

3）位移约束：如果s₁（m）→s₂（n），那么n-m≤N-M。在考虑上述约束条件后，搜索就限制在直线l₁和l₂之间的区域中，如图2-85所示。

图2-86 两个时刻的LAO46°CRAN21°造影图像及血管骨架的运动估计结果

a）原始图像 b）主要血管分支骨架 c）血管骨架的运动估计结果

用采集速率为15f／s的CAG图像序列来检验该运动估计算法，对两帧图像的结果如图2-86和图2-87所示（每隔5个像素显示一个运动向量）。由冠状动脉的解剖结构可知，血管树的各个分叉点之间应该是互相匹配的，因此对于每个血管分支，可以该分支上的分叉点作为DP的起始点。

基于弹性配准的运动估计方法没有用到任何有关目标运动或变形的先验知识或者模型，可以利用同一个相似度测量、同一个成本函数来解决不同种类的变形。并且算法的复杂度不取决于变形的复杂性，不管几何变形的复杂性如何，算法的复杂度几乎是相同的。同时，该方法对所处理的两幅图像之间的时间间隔没有严格的约束，可以计算大位移的运动向量场。因此，这种方法适合于当目标发生比较严重的变形并且变形是未知的时候对目标的运动进行估计。采用动态规划完成对最优匹配的搜索，并且引入相应的约束条件，限制可能解的搜索空间，可大大减少计算量。但是该方法需首先从原始图像中提取出血管的骨架，因而骨架提取的质量直接影响运动估算结果的准确性。

图2-87 两个时刻的RAO30°CAUD24°造影图像及血管骨架的运动估计结果

a）两帧原始图像 b）主要血管分支的骨架 c）血管骨架的运动估计结果