基于光流场的运动估计算法优化

利用CAG图像序列进行冠脉血管的二维运动分析，对于准确估计与解释心脏的运动，从而正确诊断心血管和心脏疾病十分关键，同时也是利用CAG图像进行冠状动脉树三维重建及三维运动估计的重要步骤。本节介绍三种运动估计方法：梯度光流法和特征光流法。

（1）光流基本理论

当人的眼睛观察运动物体（或物体不动，观察者运动，或两者都在运动）时，物体的景象在人眼的视网膜上形成一系列连续变化的图像，这一系列连续变化的信息不断“流过”视网膜，好像一种光的“流”，故称为光流（Optical Flow，OF）。当成像物体运动时，图像中的亮度图案也随之移动。光流是可见的亮度图案的运动，或称为表观运动。光流表达了图像的变化，由于它包含了图像运动的信息，因此可被观察者用来确定目标的运动情况。从光流的定义可以看出，由于光流有如下三个要素：一是运动（速度）场，这是光流形成的必要条件；二是带光学特性的部位（例如有灰度的像素点），它能携带信息；三是成像投影（从场景到图像平面），因而能被观察到。

如果同一个观测器，在相邻两时刻t_k-1和t_k获得的同一个三维景物图像分别为f（x，y，t_k-1）和f（x，y，t_k），而景物中某物体点在这两幅图像上的相对位置是不同的，这种位置的差是三维景物的运动反映在二维图像上的位移向量（包括大小和方向）。位移向量除以时间间隔Δt_k＝t_k-t_k-1就是瞬时位置速度。在图像序列反映的景物范围中，各物体或分部的运动是不同的，形成众多瞬时位置速度向量。这些不同的瞬时位置速度向量分布在图像上形成的向量场称为瞬时位置速度场，也即光流场。

这里需要区分两个概念：光流场和运动场。当物体在摄像机前运动，或者摄像机在环境（静态或动态）中移动时，我们就会发现图像在发生变化。在图像中观察到的表面上的模式运动就是所谓的光流场。而运动场则是三维物体的实际运动在图像上的投影，如图2-77所示，一个运动物体在空间产生一个三维运动场，运动前后空间对应点在图像上的投影形成一个二维运动场。

图2-77 运动场示意图

理想情况下，光流场和运动场互相吻合，但实际上并不如此。例如，图2-78中的理发店招牌，如果固定摄像机，那么显然所得的运动场和光流场不一致。如果招牌逆时针旋转，那么每个点的运动都是向右的，可是我们看到的条纹的运动是向上的。或者图2-79中的光滑均匀的球，若光源和摄像机都固定不动，球绕中心轴旋转，则拍摄到的图像序列中各帧的内容都是相同的，这时运动场不为零，光流场为零；若球和摄像机都固定不动，拍摄两帧图像时的光源位置不同，那么两帧图像的内容是不同的，这时运动场为零，光流场不为零。这两个例子是极端的情况，只是为了说明光流场和运动场并不总是一致的。但一般情况下，认为二者是一致的。

图2-78 理发店招牌

a）理发店招牌 b）运动场 c）光流场

图2-79 绕轴旋转的光滑球

a）光源静止，球旋转 b）球静止，光源移动

光流场的计算最初是由Horn和Schunk提出的^［59］，他们在图像序列中相邻图像之间的时间间隔很小，且图像中灰度变化很小的前提下，推导出基本的光流约束方程。设图像平面上有一点（x，y），在时刻t的灰度值为I（x，y，t），它是场景中物体上某一点（X，Y，Z）在图像平面上的投影。假定该点在t＋δt时运动到（x＋δx，y＋δy），灰度保持不变，其中δx＝uδt，δy＝vδt，u（x，y）和v（x，y）是该点光流的x和y分量，即：

I（x＋uδt，y＋vδt，t＋δt）＝I（x，y，t）（2-101）

仅有这一个约束不足以唯一地确定u和v。也可以利用各处的运动场是连续的这个事实，如果亮度随x、y和t平滑变化，可将等式的左边按泰勒级数展开，得到如下公式：

其中，e包括在δx、δy和δt中的二次以上的项。上式中约去I（x，y，t），并用δt除等式两端和取δt→0的极限后可求得如下公式：

此式实际上是dI/dt＝0的展开式，简写为如下公式：

I_xu＋I_yu＋I_t＝0 （2-104）

其中

式（2-104）就是亮度变化约束方程（Brightness Change Constraint Equation，BCCE），或称光流约束方程（Optical Flow Constraint Equation，OFCE），其中I为图像平面上一点（x，y）在时刻t的灰度值；dI／dt为运动物体的灰度随时间的变化；u＝dx／dt，v＝dy／dt分别为物体的x、y速度分量；I_x＝∂I／∂x、I_y＝∂I／∂y、I_t＝∂I／∂t分别是I对x、y、t的偏导数，它们可从图像序列中直接估计出来；（I_x，I_y）^T为图像点灰度的空间梯度，即图像中空间的灰度变化；I_t为图像的灰度随时间的变化率；（u，v）称为光流。

光流有两个分量u和v，而OFCE只有一个方程，因而不能同时求出u和v。如图2-80所示，可以把以u和v为轴的二维空间称为速度空间。满足约束方程的（u，v）值都在速度空间的直线上，但局部的测量无法辨别实际的（u，v）在约束线上的位置。也就是说由OFCE只能求出光流在亮度梯度（I_x，I_y）^T方向上的分量，公式如下：

而无法确定与梯度垂直方向（即沿等亮度线）上的分量。因此，只使用一个点上的信息是不能确定光流的，这种不确定问题称为孔径问题。为了充分确定光流，需要附加一些新的约束条件。

（2）梯度光流法

光流约束方程将物体在图像平面上投影的空间灰度变化（∂I／∂x，∂I／∂y）、图像点的灰度随时间的变化∂I／∂t、以及物体的x和y速度分量（dx／dt，dy／dt）联系起来。为了充分确定光流，需要在OFCE的基础上附加一些新的约束条件，最著名的是整体平滑性约束。Horn等^［59］根据同一运动物体引起的光流场应该是连续、平滑的，即同一物体上相邻点的速度是相似的，那么其投影到图像上的光流变化也应该是平滑的这一特点，提出了一种加在光流场上的附加约束，即整体平滑约束，利用该约束将光流的计算问题转化为一个变分问题。这个关于变化率最小的假设在一个物体内部是合理的，因为在物体内部旋转和比例变化使像素间的速度变化很小，但这样的假设在物体边界处是不正确的。

图2-80 速度空间示意图

假设对于图像平面中足够小的血管区域以及足够小的时间间隔内，两帧图像之间的运动可以用线性二维运动向量场描述。但这样图像上各点的运动就会和它们的坐标相关，导致计算出来的位移不准确。为了解决这个问题，需要寻找其他的约束条件，从而完全确定光流的两个分量（u，v）。对于图像平面中血管上足够小的感兴趣区域（Region Of Interest，ROI），在足够小的时间间隔内，两帧图像之间的运动可以认为是线性的，即：

式中，V_x和V_y是常量。

当冠状动脉管腔中充满造影剂的时候，假设两帧图像之间血管的亮度不会发生很大的变化，则有下式：

将式（2-107）和式（2-108）代入式（2-104）中，得到下式：

式中的三个一阶偏导数I_x、I_y、I_t可以从图像序列中估计出来，公式如下：

其中标号i、j和k分别对应于x、y和t。式（2-109）对于ROI中的每个像素都成立。这样就得到了由N个（N是ROI中像素的个数）方程所组成的方程组，可用矩阵的形式表示为

其中，第一个矩阵大小是N×2的，包含像素灰度的空间导数。它与一个2×1的列向量相乘，该向量中包含运动参数（V_x，V_y）。等式右边是一个N×1的列向量，它包含灰度的时间偏导数。这就产生了方程的超定问题：2个未知数，N个方程。采用最小二乘法可以很容易地求解该方程，且所花费的计算时间比常用的迭代法要少。

血管上的一点P_i从时刻t_k-1的位置（X^k-1_i，Y^k-1_i，Z^k-1_i）运动到时刻t_k的位置（X^k_i，Y^k_i，Z^k_i），时间间隔为Δt＝t_k-t_k-1。在图像平面上表现为从位置p（x_i^k-1，yk-1_i）移动到p′（x^k_i，y^k_i），其位移量为（Δx^k_i，Δy^k_i）。计算出ROI的光流（u^k，v^k）之后，就可以得到ROI的位移，公式如下：

式中，i＝1，2，…，N；N是ROI中的像素点数。也就是说，已知ROI中的一点在时刻t_k-1的位置（x^k-1i，y^k-1i）就可以计算出它在时刻t_k的位置（x^k_i，y^k_i）＝（x^k-1＋Δx^k_i，y^k-1＋Δy^ki）。设p点的瞬时速度为V^k_i，那么V^k_i的大小和方向分别为

根据亥姆霍兹（Helmholtz）理论，非刚体上任意一个有限微元的二维运动可以分解为两个正交方向上的平移、旋转和变形，微元内运动场的数学表达式如下：(www.xing528.com)

该式表达了同一点在时刻t_k的位置（x^k_i，y^k_i），与它在时刻t_k-1的位置（x^k-1_i，y^k-1_i）的关系。其中：

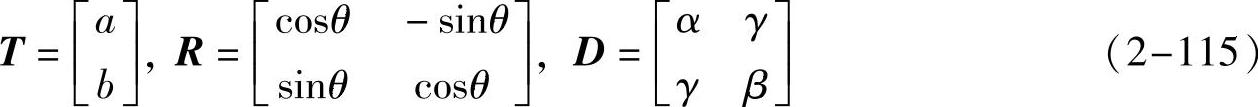
T是微元的刚性平移向量，R是旋转矩阵，D是变形矩阵。θ为像素点绕坐标原点的旋转角。显然D是对称矩阵，它的两个特征值λ₁和λ₂分别表示微元膨胀和收缩变形的量，相应的特征向量表示变形的方向。R是正交矩阵，由于是小角度的旋转，所以有sinθ≈θ，cosθ≈1，于是有下式：

代入式（2-114）中得到下式：

上述方程中包含6个未知数（a，b，θ，α，β，γ），而对于每个像素可以得到如下两个方程：

因此需要ROI中至少三个点才能解出上述方程。对ROI中的N个点，分别求出它们在下一个时刻的位置，代入式（2-117）中得到用矩阵形式表达的方程组：

采用最小二乘法分别求解式（2-119）和式（2-120），即可得到（a，b，θ，α，β，γ）的值。

Hermite矩阵D的两个特征值λ₁和λ₂分别表示微元的膨胀／收缩变形的量，相应的特征向量表示变形的方向。如假设组织的变形是线性的，且心肌是不可压缩的，令λ₁λ₂λ₃＝1，即λ₃＝1／λ₁λ₂，λ₃是垂直于心外膜表面的变形，即心室壁的增厚。λ₃是一个重要的参数，因为它包含了两个特征值λ₁和λ₂，因此仅用一个值就可以表达心外膜的收缩性。

图2-81是对从一个左冠CAG图像序列中选取的相邻两帧图像进行实验的结果，图像的采集速率为30f／s。在图2-81a中手动选择三个血管分叉点之后，用三个以这些分叉点为圆心、直径为9个像素的圆作为跟踪窗口，跟踪它们的运动。在利用梯度光流法估计运动参数之后，跟踪窗口在图2-81b中会自动标记出分叉点及其相邻像素在运动之后的位置。图2-81c、d、e分别为图2-81a中的三个ROI被放大2倍之后的显示结果。

图2-81 采用梯度光流法，用跟踪窗口对连续两帧图像进行运动估计的结果

a）第一帧图像 b）第二帧图像 c）d）e）图a）中的三个ROI被放大2倍之后的显示结果

梯度光流法的优点是：算法简单直观，不需要事先对原始图像进行二维骨架提取，就可直接进行运动估算；由于采用了基于最小二乘拟合的计算方法，因此比迭代的光流法运算速度快；线性运动场可以很容易地分解成平移、旋转和变形（收缩／膨胀）等运动分量，这些运动场反映了ROI的整体运动、旋转以及二维膨胀／收缩的模式。该方法的缺点是只能得到对目标局部的运动参数估算，无法一次获得对目标整体的运动估算。并且算法不是全自动的，需要操作者在运算开始时选择ROI。

（3）特征光流法

特征光流法即找到图像的特征（如边缘、拐角或其他位置确定的二维结构），然后跟踪它们的运动，计算特征点的光流，得到像素点的位移。包括以下两个步骤：

1）从两幅或多幅连续图像中提取出图像特征：由于特征提取会去掉图像中不重要的部分，所以会减少要处理的信息量（因而也会减少运算量），从而得到对场景更高层次的理解。

2）对各帧图像的特征进行匹配：最简单也是最常用的方法是采用两帧，对两个特征的集合进行匹配，得到一个运动向量的集合。

对于CAG图像序列，选择血管骨架作为目标特征，用二维图像点（x_i，y_i），（i＝1，2，…，N）的有序集合表示，需要确定连续两帧图像之间目标血管段骨架的运动速度（u_i，v_i）。应用全局平滑约束，使光流变化的测度最小，这里选择的测度是沿骨架的速度变化，得到如下的最小化问题：

使Φ最小的（u_i，v_i）就是所要求解的速度集。式中，V＝（u，v）是要估计的光流；n的计算公式如下：

n是垂直于边缘（即灰度梯度方向）的单位向量，即归一化的梯度向量；β是权重因子，它决定式中两部分的相对重要性；.是两向量的点积；V^⊥的计算公式如下：

V^⊥是光流沿灰度梯度方向上的分量；i＝（i_x，i_y）^T是图像点的空间灰度变化，i＝ 。所以有下式：

注意，在计算 时，应使I_x和i_y不同时为零。

式（2-121）中第一部分是骨架上相邻点的光流变化，第二部分是估算出来的光流在灰度梯度方向上的分量与由光流约束方程直接求得的光流在亮度梯度方向上分量的相似程度，它被β加权。由于血管骨架是开轮廓，且骨架点均匀分布，那么式（2-121）的离散形式为

N为骨架点的总数。使上式最小化，令：

得到方程组，用矩阵的形式表示为

式中，u＝（u₁，u₂，...，u_N）^T；v＝（v₁，v₂，...，v_N）^T；A₀＝2β·diag（n_x1.n_y1，n_x2·n_y2，…，n_xN·n_yN）^T；A₁＝2β·diag（（n_x1）²，（n_x2）²，…，（n_xN）²）＋T；A₂＝2β·diag（（n_y1）²，（n_y2）²，…，（n_yN）²）＋T；b₀＝2β·（n_x1·V^⊥₁，n_x2·V^⊥₂，…，n_xN·V^⊥_N）^T；b₁＝2β·（n_y1·V^⊥₁，n_y2·V^⊥₂，…，n_yN.V^⊥_N）^T；

其中，矩阵T中所有没标出的元素都是0。（n_xi，n_yi）由式（2-124）求出，中心线上各点灰度的时间和空间导数可由式（2-110）求出。

式（2-127）对于中心线上的每个像素都成立。A₀、A₁和A₂是N×N的方阵，b₀和b₁是N×1的列向量。这样就产生了2N个线性方程，2N个未知量。该方程为大型稀疏矩阵的线性代数方程组，而且A₀、A₁和A₂组成的矩阵是正定的，可以采用共轭梯度（斜量）法求解。其优点是，作为迭代法不必像超松弛迭代法那样选取松弛因子，而且对矩阵的元素结构也没有特殊要求（例如相容次序等）。缺点是计算过程对舍入误差比较敏感。但总的来说，用它来求解上述线性方程组，无论从存储要求或计算工作量方面来看，都不失为一个有效的方法。

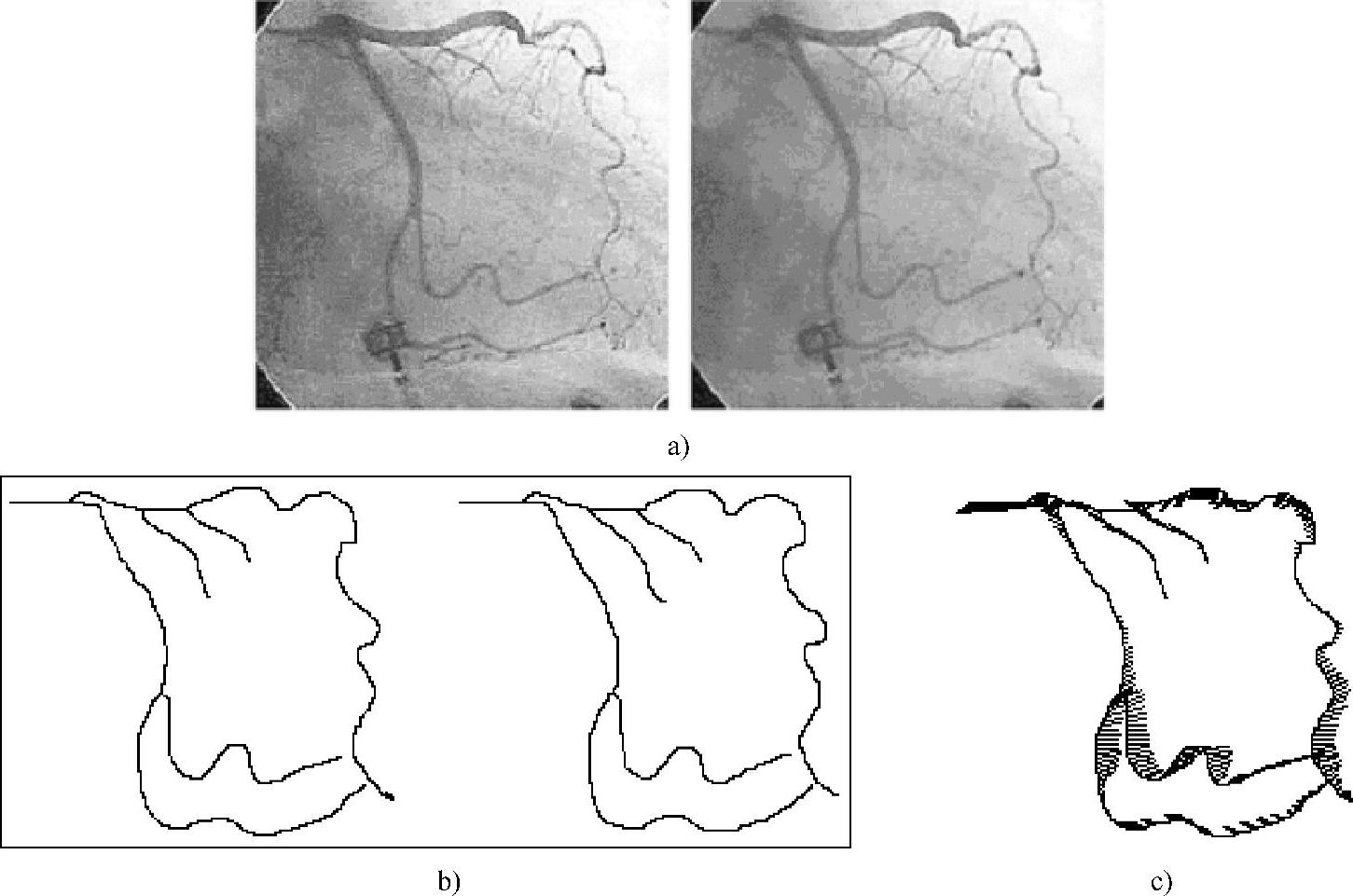
图2-82 采集速率为30f／s的左冠状动脉造影图像序列进行特征光流法验证实验的结果

a）连续两帧原始图像 b）主要血管分支的骨架 c）采用特征光流法沿血管中心线进行运动估算的结果

计算出轮廓上各像素的光流（u_i，v_i）之后，就可以由式（2-112）得到相应的位移，由式（2-113）和式（2-114）得到瞬时速度的大小和方向。图2-82是对采集速率为30f／s的左冠状动脉造影图像序列进行特征光流法验证实验的结果，图像大小为256×256像素。图2-82a为连续两帧原始图像，图2-82b是从原始图像中提取出的主要血管分支的骨架，图2-82c是采用特征光流法沿血管中心线进行运动估算的结果，其中β＝0.001，图中用线段表示各骨架点的二维运动向量，为了清晰起见，运动向量都被乘以30放大了。

与梯度光流法相比，采用特征光流法对运动图像序列中目标的运动进行估算，可以得到对目标整体的运动估算。而且除特征提取之外，其余步骤是全自动的，不需要操作者的参与。但是需事先对图像进行分割，提取出目标的特征，因此估算结果受特征提取质量的影响很大。

采用光流法进行血管骨架运动估计的优点是物理概念清晰，且不考虑特征匹配问题，在实际应用中可降低难度。其局限性在于，由于需要计算图像中像素的灰度值对x、y坐标和时间t的偏导数，因此估计结果受原图像的质量影响很大，对噪声很敏感，且抗噪性能较差；由于在光流场计算基本公式的导出过程中应用了泰勒级数展开，因此隐含着认为灰度变化以及速度场的变化都是连续的。但在实际情况中，图像中的灰度变化以及速度场都可能出现不连续，在出现这种不连续时OFCE是否仍然成立是一个值得讨论的问题；理论上只能求解灰度变化小于1个像素的连续两帧图像，而无法求得大位移情况下的光流场；要求较高的图像帧采样率；只能计算出骨架点或轮廓点的运动向量，无法得到两幅图像点之间的对应（匹配）关系。