计算血管段最小遮盖造影角度的方法优化

造影角度选择的不当不仅会使血管投影的尺寸和形态与实际不一致，而且感兴趣血管段可能被其他血管段的投影遮盖从而影响观察。因此，正如2.7.1节中分析的，尽管图2-59右图中后面三幅图像的投影方向都满足最小投影缩短，但是由于遮盖的影响，同样无法获得血管狭窄的准确值。

（1）血管遮盖的定义

投影图像中血管之间的重叠遮盖如图2-70所示，图中血管段S₁表示感兴趣血管段区域，S₂表示其他血管段，图中阴影部分为两血管段的重叠部分，其面积的大小反映了两血管相互遮盖的程度，重叠部分的面积越大，相互遮盖也就越严重。可以用重叠部分的面积与感兴趣血管段的面积百分比作为评价血管遮盖的指标，其公式如下：

式中，Area（S₁）表示感兴趣血管段的面积；Area（S₁∩S₂）表示感兴趣血管段与其他血管段相交部分的面积。常用区域内的像素数目作为区域面积的近似，即用下式近似计算血管遮盖百分比：

式中，∏（S₁）和∏（S₁∩S₂）分别表示血管段S₁和S₁与S₂相交区域内的像素总数。

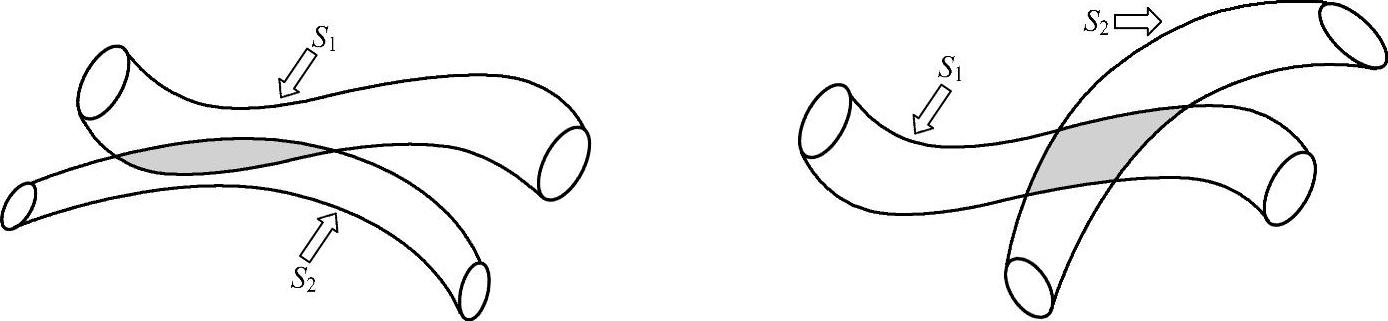
图2-70 血管之间遮盖示意图

（2）感兴趣血管段最小遮盖的计算

设C_i（t）＝（x_i（t），y_i（t），z_i（t））（t∈［0，1］）为用B样条曲线表示的各三维血管段的骨架，L_i（i＝1，2，…，n）是以C_i（t）为中心线、完成表面重建的血管段，S_i是L_i在造影角度（α，β）下的投影，n为血管段的数目，L_k为感兴趣血管段，造影角度为（α，β），其遮盖百分比可由下式计算：

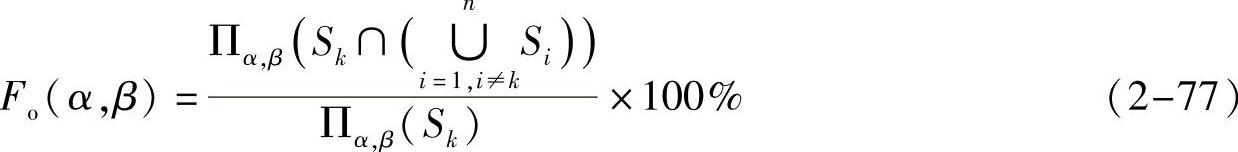
式中，Πα，β（S_i）表示在造影角度（α，β）下L_i的投影S_i包括的像素数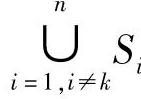； 表示其他血管段在投影图像上的像素。设Ψ₁为满足L_k最小投影缩短的造影角度（α，β）的范围，则同时满足最小投影缩短和最小遮盖的造影角度（即最佳视角）可通过使F_o最小化获得，公式如下：

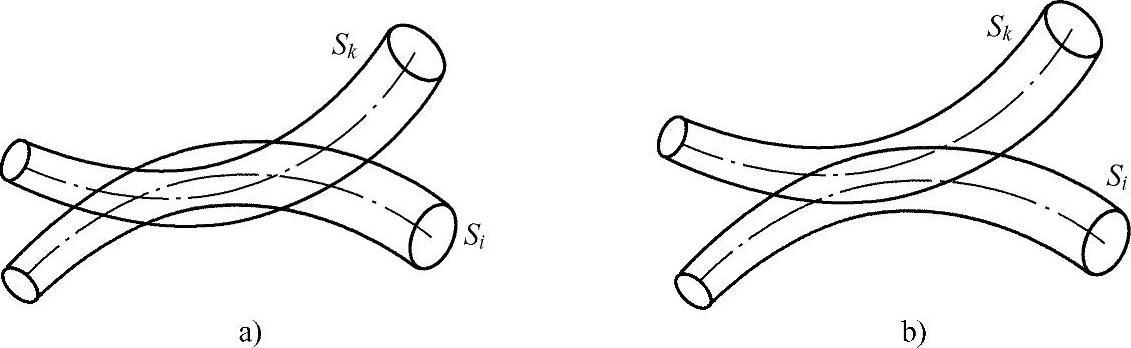
为了进一步降低计算量和算法复杂度，可以把血管间的遮盖分为如图2-71所示的两种情况。在计算满足最小遮盖的造影角度时，如果在角度（α，β）下的投影图像中S_k的中心线c_k（t）和S_i的中心线c_i（t）相交，则S_i必然会对S_k形成遮盖，即该造影角度不满足最小遮盖。设Ψ₁表示满足感兴趣血管段L_k最小投影缩短的角度范围，那么对于Ψ₁中的角度，可以通过计算在其相应的投影图像中感兴趣血管段中心线与其他血管段中心线的相交情况进一步缩小Ψ₁的范围。即如果在角度（α，β）∈Ψ₁下的投影图像中存在与c_k（t）相交的其他血管段中心线c_i（t）（i≠k），则把该角度从Ψ₁中去除，得到角度集合Ψ₂，公式如下：

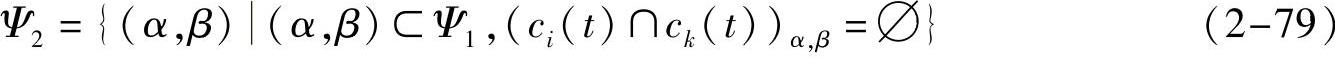
显然，对于Ψ₂中的造影角度，在其投影图像中，感兴趣血管段都满足最小投影缩短，且c_k（t）与c_i（t）没有交点，但是还可能存在如图2-71b所示的血管重叠，因此需要在Ψ₂中继续寻找最佳视角。

(www.xing528.com)

图2-71　血管间遮盖情况示意图

a）两血管段中心线相交 b）两血管段中心线不相交但区域重叠

对于图2-71b所示的血管重叠情况，首先在图像中定义一个包括感兴趣血管段的矩形区域，如图2-72所示，图中S_k为感兴趣血管段L_k的投影，S_i为血管段L_i的投影，图2-72a中S_i的中心线和矩形区域边界相交于两点A和B。矩形区域的大小l×h为能够完全包括感兴趣血管段的区域，为了防止出现S_k与S_i重叠，但S_i的中心线与矩形区域不相交的情况，即如图2-72b所示的情况，将矩形区域放大为（l＋δ）×（h＋δ），其中：

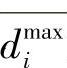
为S_i的最大直径。显然，矩形区域经过上述放大后，只有当S_i的中心线c_i（t）与矩形区域边界有交点时，S_i才有可能对S_k形成遮盖，并且只有两个交点（即图2-72a中的点A和B）之间的血管段会对S_k形成遮盖。用l_i（i＝1，2，…，m₀）表示点A和B之间的血管段中心线，在l_i上均匀选取m₃i个点 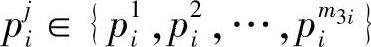，点p^j_i处的二维血管半径为r^j_i（j＝1，2，…，m_3i）。同样，在c_k（t）上均匀选取m₁个点p_l（l＝1，2，…，m₁），r_l为其对应的血管半径。在计算血管遮盖时，只需要考虑l_i所对应的血管段对S_k的遮盖情况。在图2-72a中，l_i中的点p_ji与p_l中各点的距离最小值为

设式（2-81）取最小值时对应p_l中的点为p_u，如果满足下式：

则S_i会对S_k形成遮盖；如果l_i中的所有像素都不满足式（2-82），则在该造影角度下的投影图像中其他血管段都不会对感兴趣血管段形成遮盖，此时的造影角度同时满足最小投影缩短和最小血管遮盖，即为最佳视角。

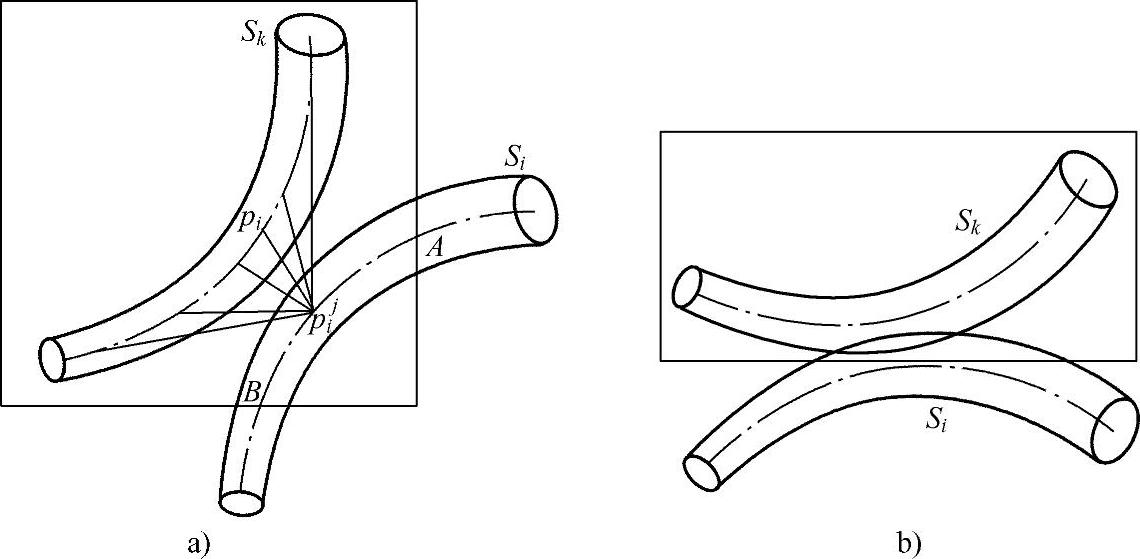
图2-72 包括感兴趣血管段的矩形区域

a）血管不重叠 b）血管重叠

在临床诊断中，其他血管段虽然没有对感兴趣血管段形成遮盖，但距离感兴趣血管段过近，同样会影响医生对感兴趣血管段的观察和测量，因此在满足最小遮盖的投影图像中，需要使其他血管段与感兴趣血管段有一定的距离，即对式（2-82）进行修正得到如下公式：

其中，ε为大于0的常数。

前面介绍了两种计算血管最小遮盖的方法，式（2-78）的计算方法具有普遍意义，但是其计算量大，算法复杂；第二种计算方法不需要提取血管区域和计算具体的遮盖百分比，它首先利用其他血管段中心线与感兴趣血管段中心线的相交情况把血管遮盖分为两种情况，然后再利用其他血管段中心线与感兴趣血管段中心线的距离来进一步判断其他血管段对感兴趣血管段的遮盖情况，从而获得满足最小遮盖的造影角度，这种算法简单，计算量小。由于上述两种算法都是在满足最小投影缩短的造影角度范围内计算最小遮盖，因此获得的造影角度即为感兴趣血管段的最佳视角。