计算最小造影角度以满足感兴趣血管段投影缩短需求

由于可用造影角度来表示投影方向，因此获取感兴趣血管段的最佳投影方向也就是寻找最佳造影角度（最佳视角），一般是先获取满足最小投影缩短的造影角度范围，然后再寻找满足最小血管遮盖的造影角度。

满足感兴趣血管段最小投影缩短造影角度的计算方法主要包括几何法、血管投影缩短最小化法和平面拟合法。为了表述方便，本节所提到的最佳视角均指满足最小投影缩短的造影角度。

（1）几何法

利用几何方法获取满足最小投影缩短的造影角度时，需要包含感兴趣血管段的两幅同一时刻不同造影角度的图像，在每幅图像中指定感兴趣血管段的起点和终点，由此两点和造影图像对应的X射线源构成平面，即图2-68中的平面S₁p₁₁p₁₂和S₂p₂₁p₂₂，两个平面的交叉线p₁p₂即为感兴趣血管段的三维位置，垂直于该交叉线中心的投影方向即为最佳投影方向。满足最小投影缩短的造影角度范围^［53］如图2-69所示，图中两条曲线分别是两段血管的满足最小投影缩短的造影角度范围，由于机械等方面的限制，一般只能取图中阴影部分的造影角度。当感兴趣血管段是分支血管时，其最佳视角为同时满足各分支最小投影缩短的造影角度，即图中两曲线的交点。

几何法的优点是不需要进行三维重建，运算速度快，但是它对于相对曲折的血管段误差较大。

图2-68 几何法计算最佳视角的示意图

图2-69 满足最小投影缩短的造影角度范围^［53］

（2）血管投影缩短最小化法

在三维重建冠状动脉树的基础上，利用B样条曲线拟合感兴趣血管段的三维骨架，通过曲线的曲率和挠率来控制血管段上点的选择，并利用曲线在所选点处的切矢量作为血管段在该点处的方向矢量，通过使血管投影缩短最小化来获得满足感兴趣血管段最小投影缩短的造影角度。

设C（t）＝（x（t），y（t），z（t））（t∈［0，1］）为用B样条曲线表示的感兴趣血管段L的三维骨架，其形状变化可以用曲率和挠率来描述。设C（t_j）（j＝1，2，…，m）表示在C（t）上选取的m个点。利用曲率和挠率来控制参数t_j的选取，公式如下：

即在曲率和挠率较大的地方多选点，反之则少选。式中，△为步长，m的选取方法是：如果t_i＜1且t_i＋1≥1，则m＝j＋1，t_m＝1。k_j-1是步长权重参数，其计算公式如下：

(www.xing528.com)

式中，κ_i-1和τ_i-1分别是C（t）在t_j-1点处的曲率和挠率；κ_max和τ_max分别是C（t）的最大曲率和挠率；λ和η是权重参数。

已知造影角度（α，β），血管段L的投影缩短百分比F_f为

式中， 是曲线C（t）在t_j点处的切向量， 表示 的模；0°≤θ_j≤90°是 和投影向量 之间的夹角； ＝（-cosβsinα，-sinβ，cosβcosα）。通过使F_f最小化即可获得满足血管段L最小投影缩短的造影角度（α，β），公式如下：

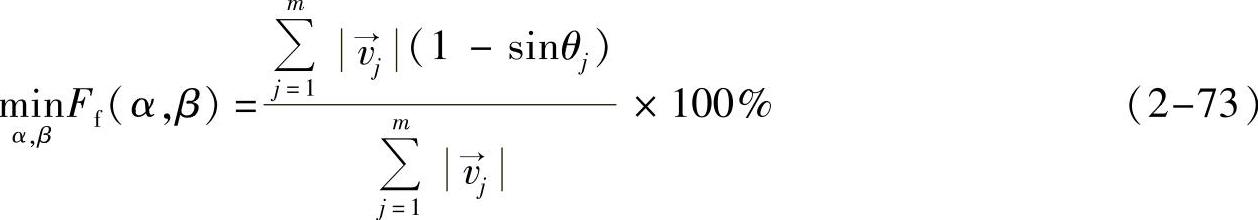
当感兴趣血管段是多分支血管段（例如血管分支）时，设L＝｛L₁，L₂，…，L_k｝为选取的k支血管段，则可利用下式获得满足血管段L最小投影缩短的造影角度（α，β）：

式（2-73）和（2-74）中，-90°≤α≤90°；-45°≤β≤45°；0°≤θ_ij≤90°是 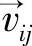和投影向量 之间的夹角； （j＝1，2，…，m_i）是血管段L_i上的切向量；m_i是在L_i上均匀选取的点。

（3）平面拟合法

实际应用中，医生关心的仅是血管狭窄附近的病变状况。因此，可选取血管狭窄附近的血管段为感兴趣血管段，在对感兴趣血管段进行三维重建和B样条曲线拟合后，按照式（2-70）在感兴趣血管段上选取m个采样点，这些采样点可近似拟合到一个平面上，则平行于拟合平面的法向量方向就是满足感兴趣血管段最小投影缩短的投影方向。

利用平面拟合法来获取满足最小投影缩短的造影角度时，计算精度很大程度上取决于平面拟合的精度，可利用最小二乘法或者最佳平面拟合法来获得采样点的拟合平面。前者是令采样点与拟合平面之间的误差平方和最小得到拟合平面的参数，后者是使拟合平面尽可能逼近选取的采样点，即希望采样点与拟合平面间的最大偏差达到最小，满足这种要求的拟合平面即为最佳拟合平面。

本节介绍了三种满足感兴趣血管段最小投影缩短最佳造影角度的计算方法，这三种方法各有优缺点，具体见表2-2。它们可应用于不同的场合，例如，在对精度要求不高且感兴趣血管段是近似直血管段的情况下，可以选用几何法；在精度要求较高且感兴趣血管段结构比较复杂的情况下，可以选用血管投影缩短最小化法或平面拟合法。

表2-2 三种满足感兴趣血管段最小投影缩短的最佳视角计算方法的比较