表面三维重建技术优化与应用

从二维投影图像重构血管三维形态的过程中，两个角度的造影图像所提供的数据非常有限，重构血管表面的难度相当大，因此必须简化目标，降低问题的复杂性和难度。理想状况下冠状动脉可以被看做一个弯曲的空间管状系统，并可假设为由二维圆盘（或椭圆盘）沿着三维曲线行走形成的“广义的圆柱体”（generalized cylinder，GC）^{［36，43］}。

冠状动脉三维简化模型如图2-36所示，其中虚线表示血管的骨架（即中心线），血管骨架贯穿一系列圆盘（或椭圆盘）的中心，并且垂直于圆盘，于是冠状动脉的三维模型可以用图2-36中右图所示的三维骨架和圆盘描述。通过计算各骨架点处血管腔的三维直径，得到限制血管横截面的轮廓，然后根据血管横截面为椭圆的假设推导椭圆方程，同时解决相邻血管横截面相交的问题，即可重建血管腔的三维表面，并进行三维结果的绘制和显示。

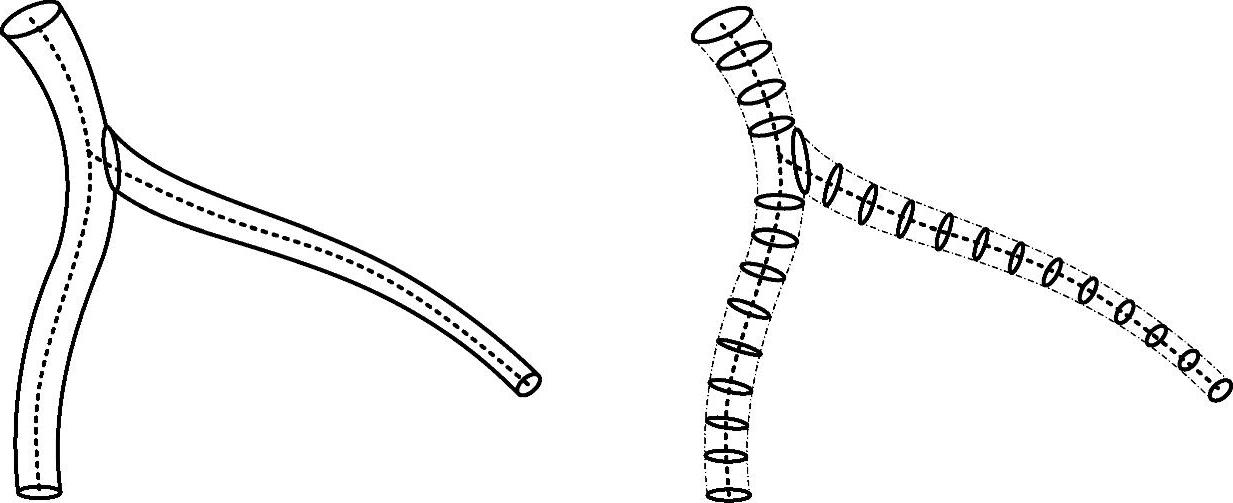
图2-36 冠状动脉的三维简化模型

（1）计算血管腔的三维直径

造影系统的投影成像可以看成如图2-37所示的透视投影，其中S₁为X射线源，O₁表示造影图像A的中心，P₁为坐标系X₁Y₁Z₁S₁中的三维空间点P（其坐标为（x₁，y₁，z₁））经透视投影到图像A上的点，p₁在图像平面坐标系U₁V₁O₁中的坐标为（u₁，v₁）。由于透视投影的放大成像原理，图像中血管投影的二维直径一般要大于血管的真实直径。设图像A中点p₁处的二维血管直径为d₁，则可以根据图中的成像几何关系计算出P点处血管在该方向的三维直径d，公式如下：

其中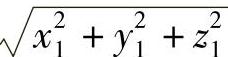， 表示坐标系X₁Y₁Z₁S₁中点P到点S₁的距离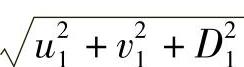， 是坐标系X₁Y₁Z₁S₁中点p₁到S₁的距离。

（2）血管横截面模型

正常冠状动脉血管腔的横截面呈圆形或椭圆形，但是当血管变得狭窄时管腔形状的改变通常是复杂多样的，狭窄多为偏心型或不规则型，常见的如月牙形和星形^［44］，如图2-38所示。由于冠脉造影图像的本质是投影成像，无法准确表达狭窄血管横截面的具体形状，所以在重建血管腔表面时一般假设血管横截面为圆形或椭圆形，根据两个角度的二维管腔直径信息进行适当的近似描述。本节根据造影系统的投影模型研究血管横截面的椭圆模型，并在此基础上推导非正交造影图像情形下血管横截面的椭圆方程。

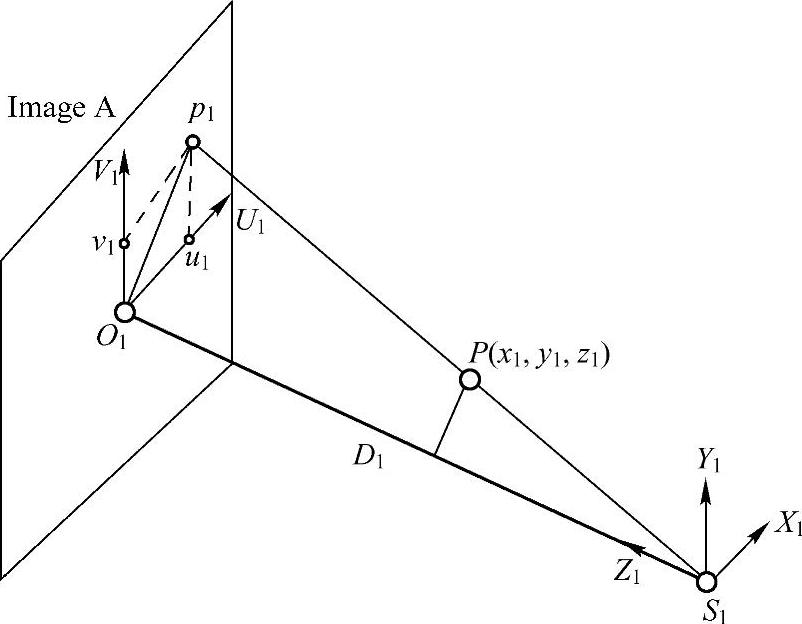
图2-37 造影系统的透视投影图

图2-38 血管横截面的形状^［44］

造影成像系统分别在两个角度对点P处的三维血管进行透视投影成像，如图2-39所示，点S₁和S₂表示X射线源，分别成像于图像A和B，O₁和O₂为图像中心，两个中心投影轴S₁O₁和S₂O₂之间的夹角为φ；点P分别投影到图像A的点p₁和图像B的点p₂，p₁和点p₂处血管投影的半径分别为r₁和r₂；投影线S₁p₁和S₁O₁之间的夹角为φ₁，投影线S₂p₂和S₂O₂之间的夹角为φ₂。两束X射线相交形成图中黑框所示的楔形区域，由投影关系可知，点P处血管的横截面一定在该区域内。

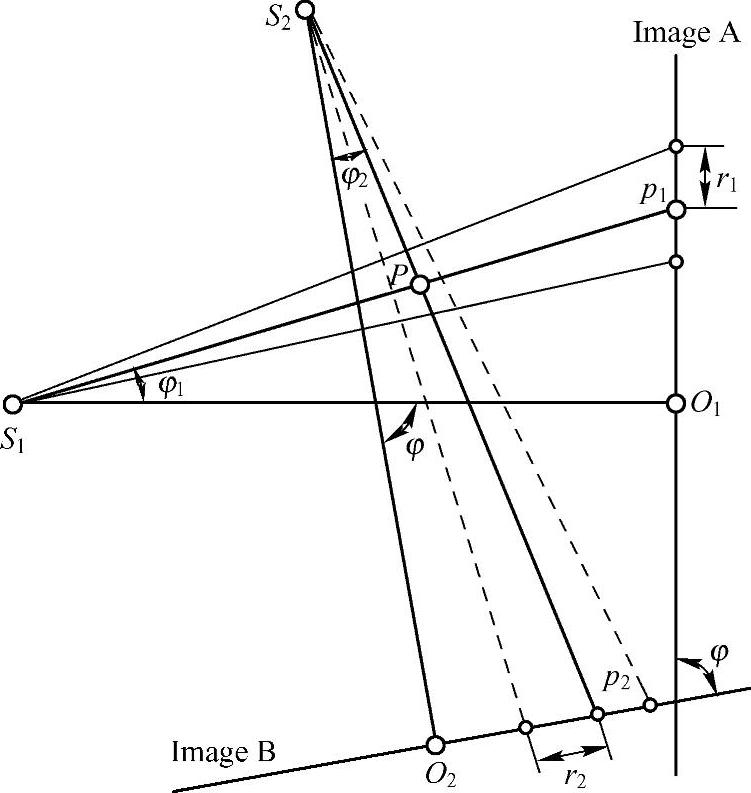
图2-39 造影系统在两个角度的透视投影图

由于冠状动脉的直径远小于X射线成像距离，所以可以将图2-39中限制血管横截面的楔形区域简化为以点P为中心的平行四边形，如图2-40所示。其中实线表示经过点P的投影线 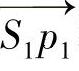和 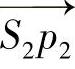，并且分别平行于平行四边形的两对边；两条虚线分别平行于图像A的直线 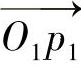和图像B的直线 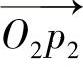，如图2-39所示。由图2-39中的角度容易推算出图2-40中平行四边形的角度θ，公式如下：

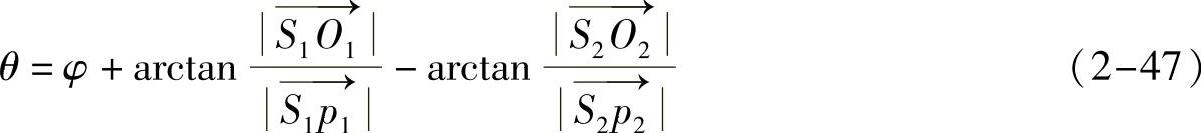
根据式（2-47），可以由图2-39中的二维血管半径r₁和r₂计算点P处的血管在投影线 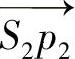和 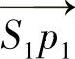方向的直径分别如下：

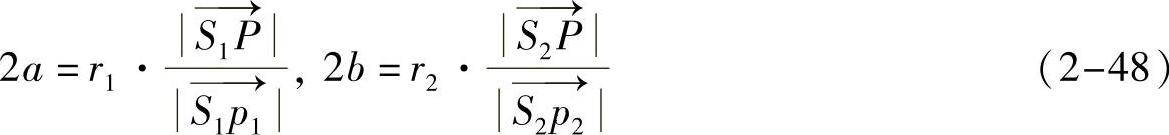
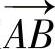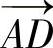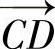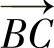控制血管横截面形状的平行四边形可以用图2-41的平行四边形ABCD表示，边 和 的夹角g由式(2-48)计算得到，边 和 之间的距离为2a，边 和 之间的距离为2b。由此确定椭圆形的血管横截面，并使得椭圆横截面内切于平行四边形ABCD。

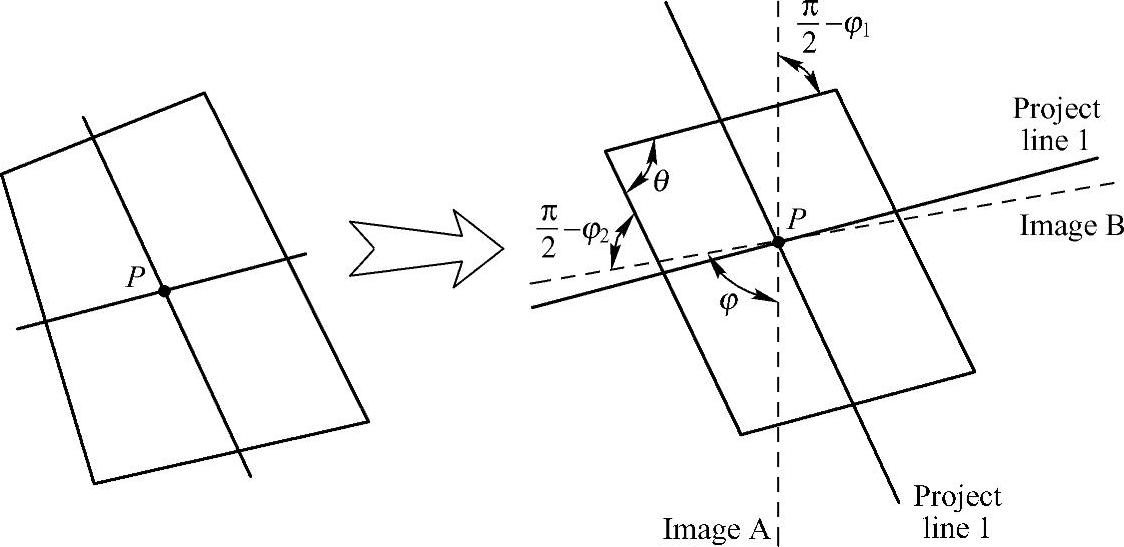
图2-40 血管横截面的模型简化图

但是，内切于平行四边形的椭圆并不唯一，也就是说由平行四边形ABCD确定血管的椭圆横截面是多义性的问题。解决这一问题的方法主要有以下三种：第一，利用三个角度的血管直径信息得到唯一的椭圆形的血管横截面^［45］，如图2-42所示。该方法要求三维血管骨架的重建精度较高，而且三个角度之间的几何变换关系也会影响椭圆横截面的计算精度，所以将该方法应用到基于单面造影图像的血管三维重建中比较困难；第二，根据二维血管边缘对椭圆方程进行优化，得到较理想的椭圆方程^［46］，如图2-43所示，由三维血管骨架计算点P处的法向平面，分别将两幅图像的血管边缘反投影，反投影线和法向平面相交得到四条曲线，然后根据这四条曲线进行优化，使得曲线上的点到椭圆的距离之和最小，从而确定椭圆方程的参数。该方法的计算量较大，实现过程比较复杂；第三，因为用于重建血管横截面的数据有限，只能给出血管横截面的近似椭圆，所以可以使椭圆的一条轴和投影线平行，如图2-41所示，这样就可以计算出唯一的椭圆方程。和前两种方法相比，该方法比较简单，容易实现

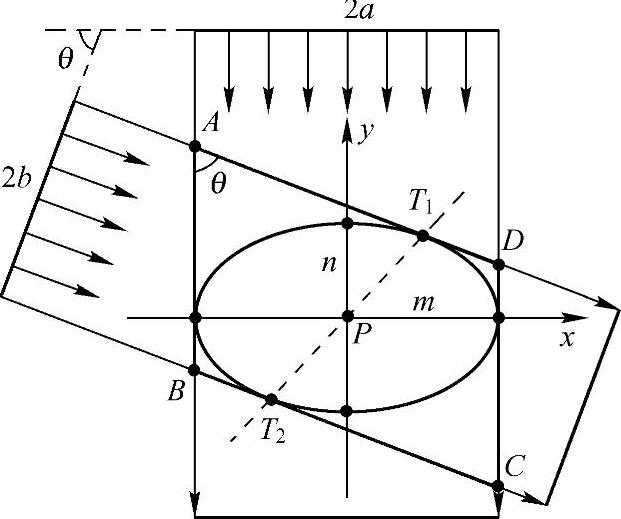
图2-41 血管的椭网横截面模型

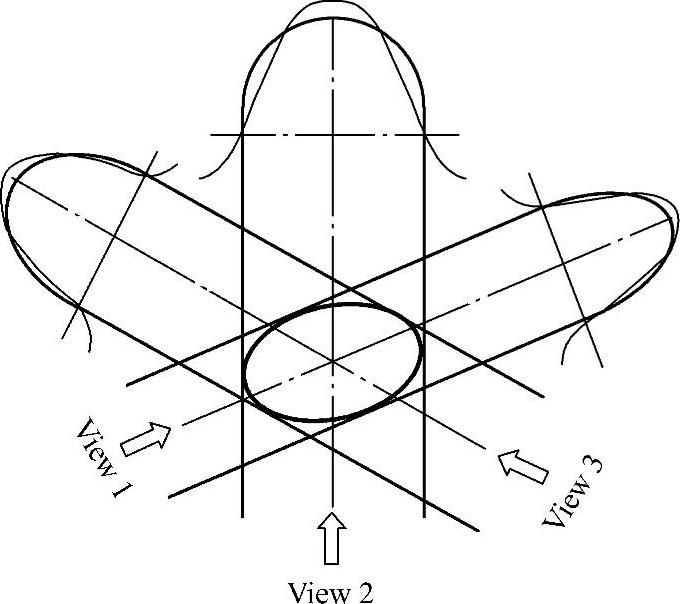
图2-42 三个角度的血管椭圆横截面模型^［45］

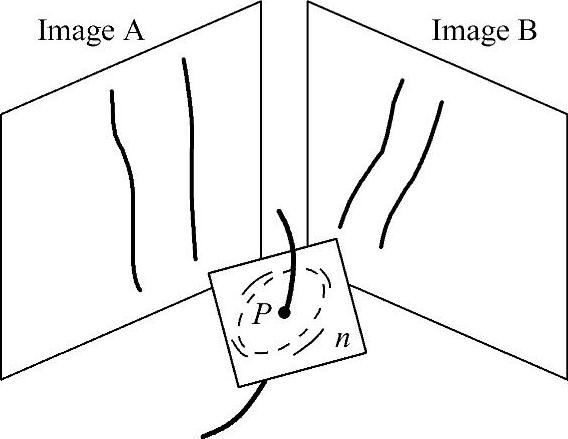
图2-43 血管椭圆横截面的优化模型^［46］

（3）相邻横截面的顶点融合

由于冠脉血管树的结构很复杂，血管分支处和弯曲程度较大的血管处通常会出现表面自相交的情形。目前现有的解决方法主要包括：

1）利用相互平行的椭圆横截面重建血管表面^［47］，该方法比较简单，没有考虑相邻血管横截面相交的情况，仅适合描述弯曲程度不大的一段血管。

2）利用可变形模型重建三维血管表面^［48］，可实现血管分支的重建，但实现过程比较复杂。

3）顶点融合方法^［10］，根据矢量间的夹角判断是否相交，将两个相邻轮廓上相交的对应顶点融合为一个顶点，避免表面的自相交。

下面介绍顶点融合方法的基本原理，其示意图如图2-44所示，图2-44a中a₁和a₂是三维骨架点，v₁₁和v₁₂是a₁点处椭圆轮廓的采样点，v₂₁和v₂₂是a₂点处椭圆轮廓的采样点。由于两个椭圆轮廓在v₂₁和v₁₁点相交，所以为了正确地重建血管表面，需要将v₂₁和v₁₁融合为一个顶点。根据对应顶点连线的矢量可以判别椭圆轮廓是否相交，是否需要融合顶点，如图2-44b所示，如果矢量 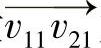为零，则不必融合；反之，设 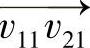与 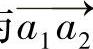之间的夹角为

若γ∈［π／2，π］，则说明两个横截面相交，需要将顶点v₁₁和v₂₁融合。

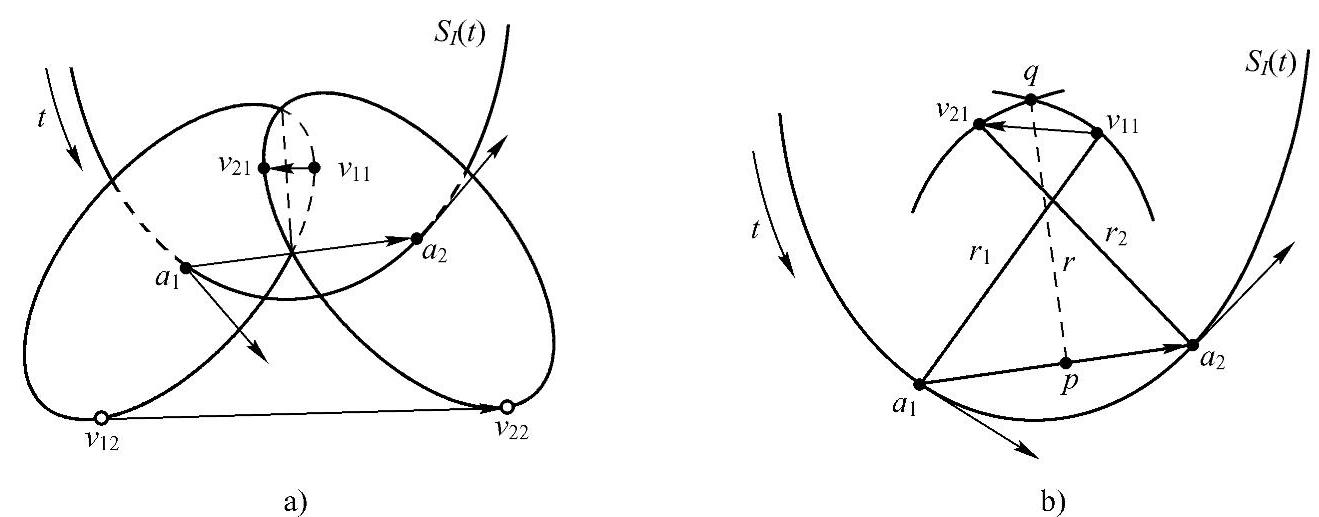
图2-44 顶点融合示意图(www.xing528.com)

a）横截面相交的判别；b）顶点融合示意图

（4）重建三维表面

至此，已经得到了血管的三维B样条骨架，以及骨架点处血管的椭圆横截面，如图2-45所示。重构三维血管表面也就是要将相邻的椭圆横截面连接起来，构成一个封闭的曲面，主要有三种方法：球包络方法、三角形拼接方法和NURBS曲面拟合法。

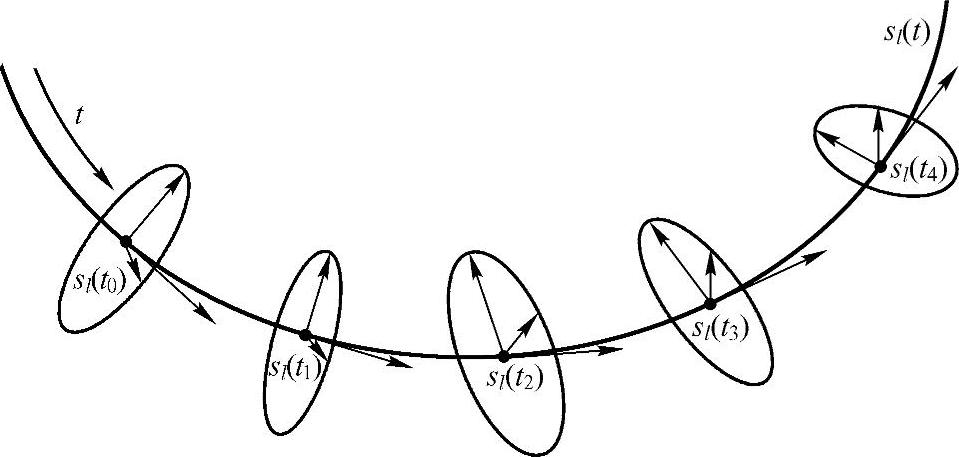
图2-45 B样条三维骨架和椭圆横截面示意图

球包络方法的基本原理是采用一系列椭球沿三维血管骨架行走，用一系列椭球的包络来表示血管的三维表面。该方法比较简单，易于绘制，重建出的管状结构过渡平滑，且拓扑结构保存完好。但是其重构效果与三维血管骨架点的采样率有很大关系，当采样率足够大时重构的血管表面比较平滑，相反则相邻椭球之间会出现凹陷，影响重构效果，如图2-46所示，左图为三维血管骨架，其后三幅图为椭球包络重构的血管表面，可见随着骨架点采样率的增大，表面重建的效果越来越好。另外，该方法只能表现两个角度的血管直径，灵活性较差。例如冠状动脉狭窄部位的形状很不规则，采用球包络方法就难以准确表达其形态。

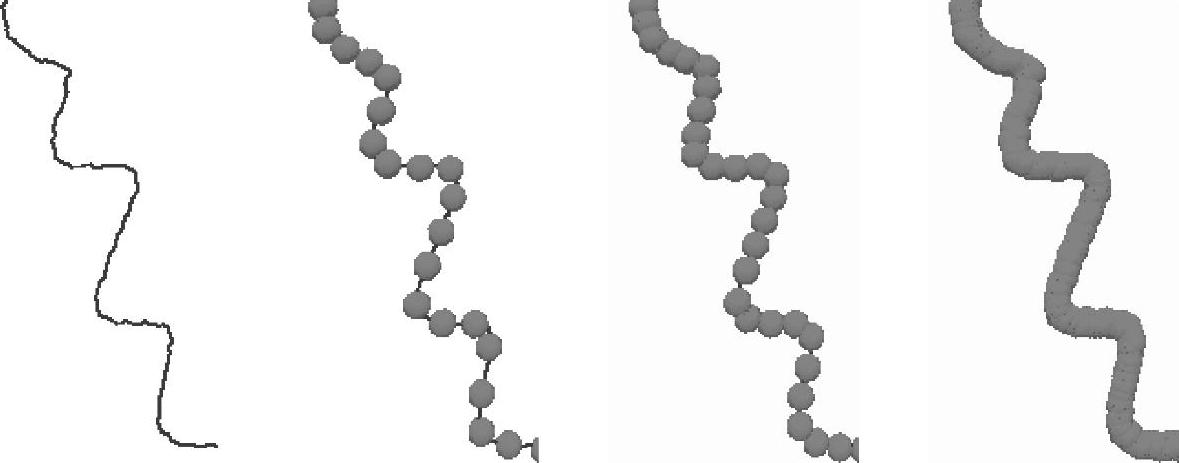
图2-46 不同采样率的球包络表面重建结果

对图2-47a所示的两幅近似垂直角度的左冠状动脉造影图像重建三维重建血管骨架，并采用球包络方法重构血管表面，结果如图2-47b所示。

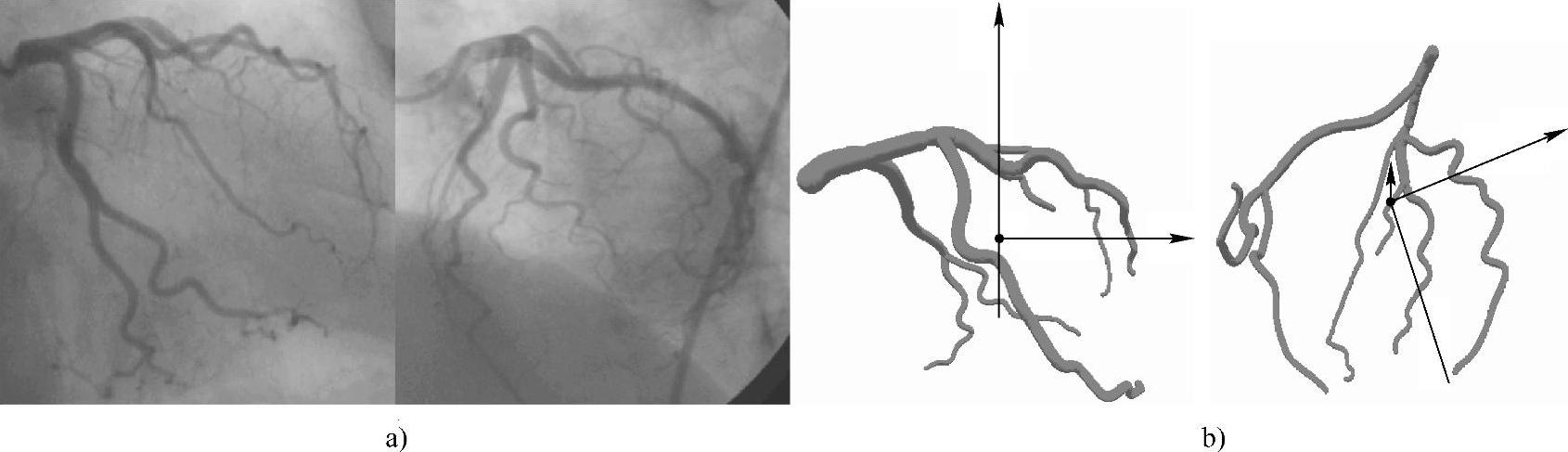
图2-47 对近似正交的一对左冠CAG图像进行血管三维重建的结果

a）两幅造影角度分别为RAO30°CAUD24°和LAO46°CRAN21°的左冠造影图像 b）采用球包络方法重建血管表面结果

三角形拼接方法（又称三角面片重构表面方法）即将椭圆横截面轮廓简化为多边形，然后用三角面片将相邻横截面多边形的点列连接起来，构成一个封闭的曲面。其示意图如图2-48所示，假设两相邻椭圆横截面上各有一条轮廓线，按逆时针方向排列的上、下轮廓线的点序列分别为｛P₀，P₁，…，P_m-1，｝和｛Q₀，Q₁，…，Q_n-1，｝。如果将上述点序列分别依次用直线段连接起来，则得到这两条轮廓线的多边形近似表示，每一个直线段P_iP_i＋1或_jQ_j＋1称为轮廓线线段，连接上轮廓线一点与下轮廓线一点的线段称为跨距^［49］。一条轮廓线段以及将该线段两端点与相邻轮廓线上一点相连的两段跨距构成一个三角面，称为基本三角面，这两段跨距则分别称为左跨距和右跨距。相邻轮廓之间三维表面的重构就是用一系列相互连接的三角面片将上下轮廓线连接起来。图2-49是采用三角面片重构血管三维表面的网络图，图2-49a中血管曲率较小，所以不存在相邻血管横截面相交的情况，图2-49b中血管曲率较大，采用顶点融合方法能很好地处理血管横截面相交的问题。对图2-47a所示的两幅造影图像采用三角形拼接法重构血管表面的结果如图2-50所示。

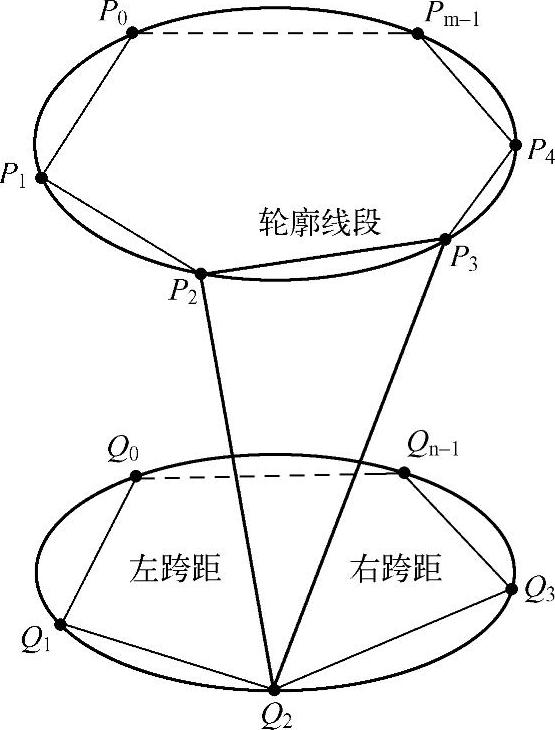
图2-48 三角形拼接法示意图

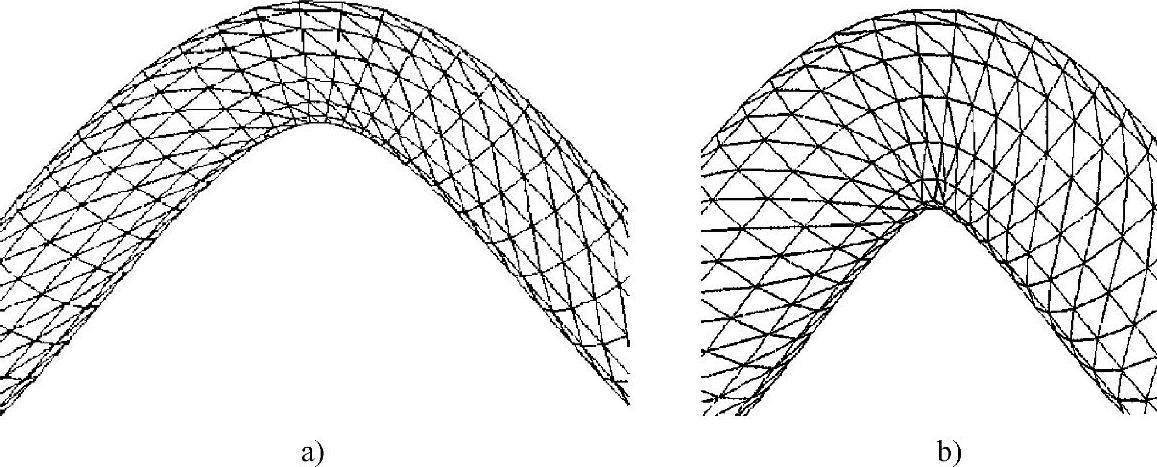
图2-49 采用三角拼接法重构出的血管表面网络

a）无顶点融合 b）存在顶点融合

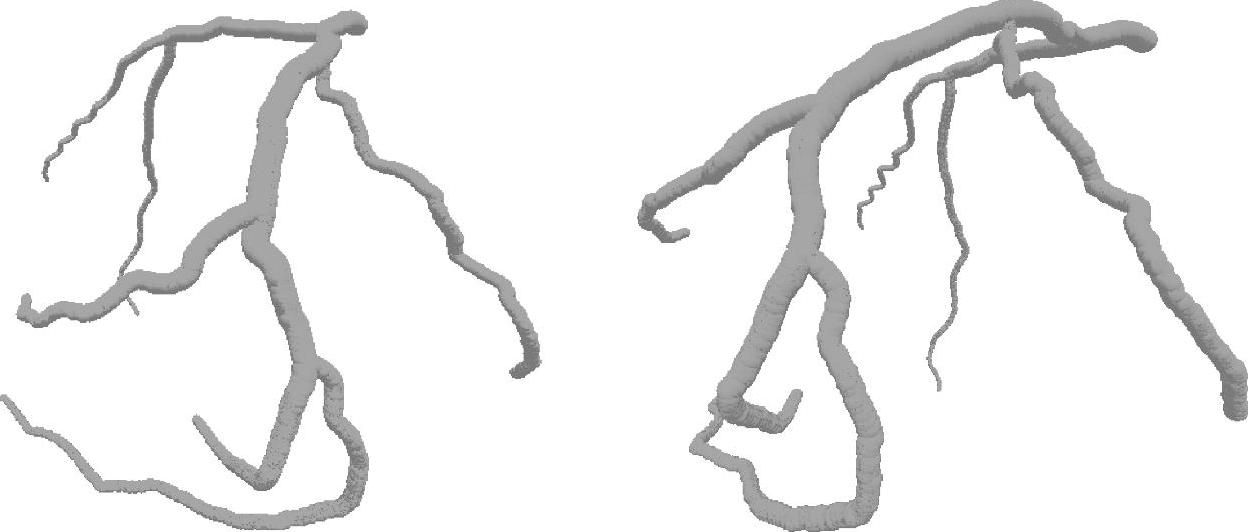
图2-50 三角形拼接法重构冠状动脉血管表面的结果

三角形拼接法是比较成熟的表面重建技术，由于采用三角形为基元，因而重建速度快，重建结果也比较光滑。其不足之处在于重建效果与血管骨架点的采样率有关，且局部表达能力不强，尤其对狭窄的冠状动脉部分血管表面的表达效果不理想。

NURBS（非均匀有理B样条曲线）曲面拟合方法即采用NURBS曲面拟合椭圆横截面上的采样点，得到用NURBS曲面表示的三维血管表面。NURBS是非均匀有理B样条（Non-Uniform Rational B-Splines）的缩写，NURBS曲线和曲面是计算机图形学和计算机辅助设计中最受欢迎的几何建模方法之一。NURBS曲面具有良好的连续性、光滑性、仿射不变性、透视不变性和局部控制等优良特性。

p×q次NURBS曲面的表达式如下^［42］

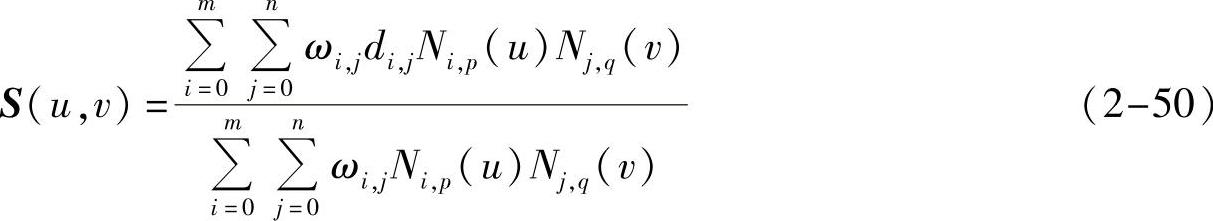
式中，d_i，j（i＝0，1，…，m；j＝0，1，…，n）是控制顶点，呈拓扑矩形阵列，形成一个控制网络；ω_i，_j是与顶点d_i，j联系的权值；N_i，p（u）和N_j，q（v）分别是参数u方向p次和参数v方向q次的规范B样条基函数，它们分别由u向和v向的节点矢量U＝［u₀，u₁，…，u_m-p＋1］与V＝［v₀，v₁，…，v_n-q＋1］按de Boor-Cox递推公式决定。N_i，p（u）的递推公式定义如下：

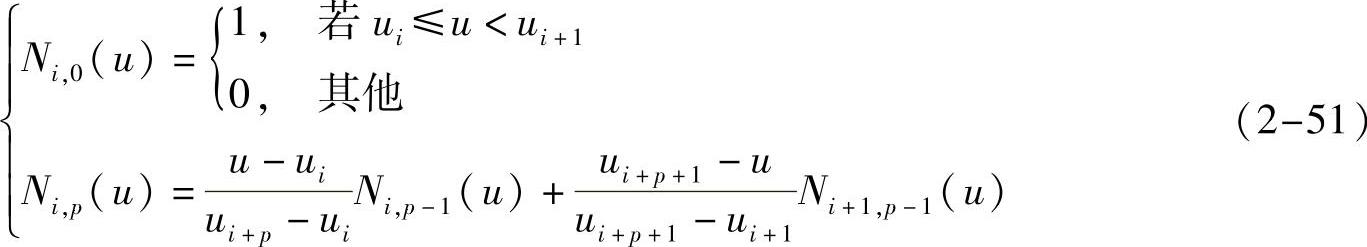
其中规定0／0＝0，N_j，q（v）的递推公式类似。

由NURBS曲面方程可知，通过调整控制顶点和权值，可以灵活地改变曲面的形状，而且个别控制顶点和权值的调整只改变曲面的局部形状。冠状动脉可以看成一个空间连续、光滑、弯曲的管状系统，因此NURBS曲面非常适合表示冠状动脉血管表面，尤其是局部控制特性给冠状动脉狭窄部分的准确表示提供了方便。

NURBS曲面拟合方法虽然比较复杂，计算量较大，但灵活性好，表现狭窄冠状动脉三维表面的能力比较强。对图2-47a所示的两幅造影图像采用NUBRS曲面拟合法重构血管表面的结果如图2-51所示，圆圈内的动脉存在中度狭窄。对图2-52a所示的两幅左冠状动脉造影图像，采用NURBS曲面拟合方法重建三维血管，结果如图2-52b所示，其中左旋支的分支点处存在明显狭窄。

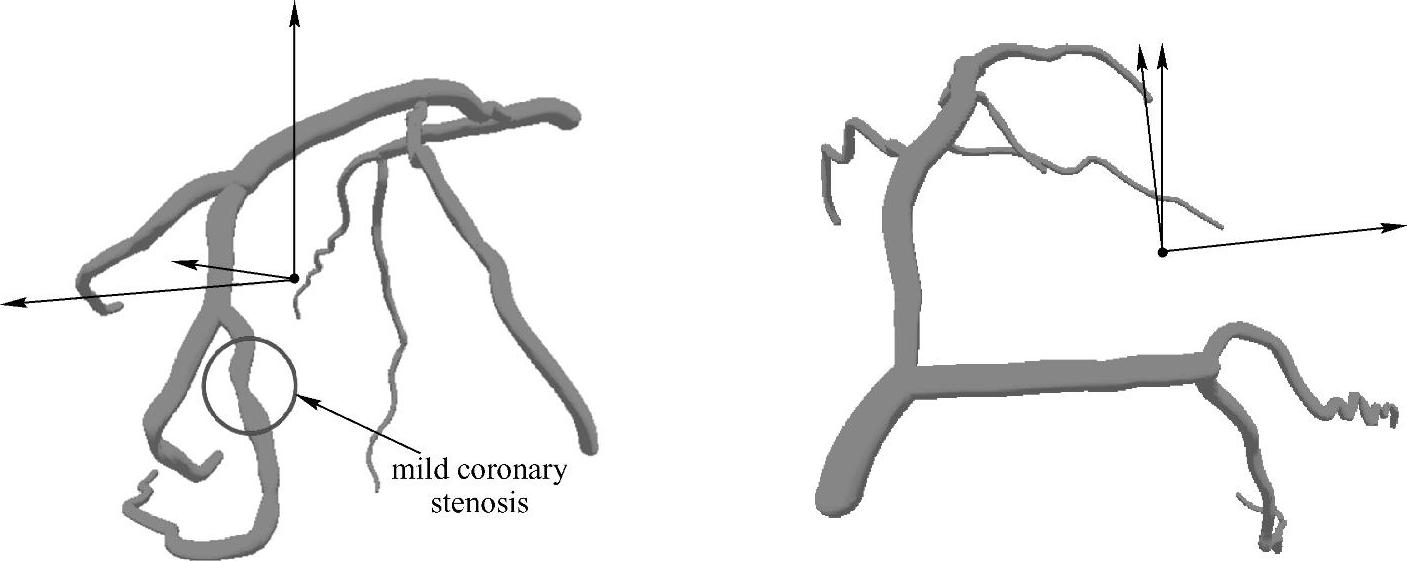
图2-51 采用NURBS曲面拟合方法重构冠状动脉树表面的结果

分别采用球包络法、三角形拼接法和NURBS曲面拟合的方法进行血管表面的重建，将结果局部放大比较，如图2-53所示，可以看出，三种方法重建的血管形态相同，但图2-53c所示血管的光顺性明显好于图2-53a和图2-53b。实际应用过程中，应根据具体要求选择合理的表面重建方法，例如重构狭窄动脉表面时可选择NURBS曲面拟合法；如果要求实时显示重建结果则可选择三角形拼接法。

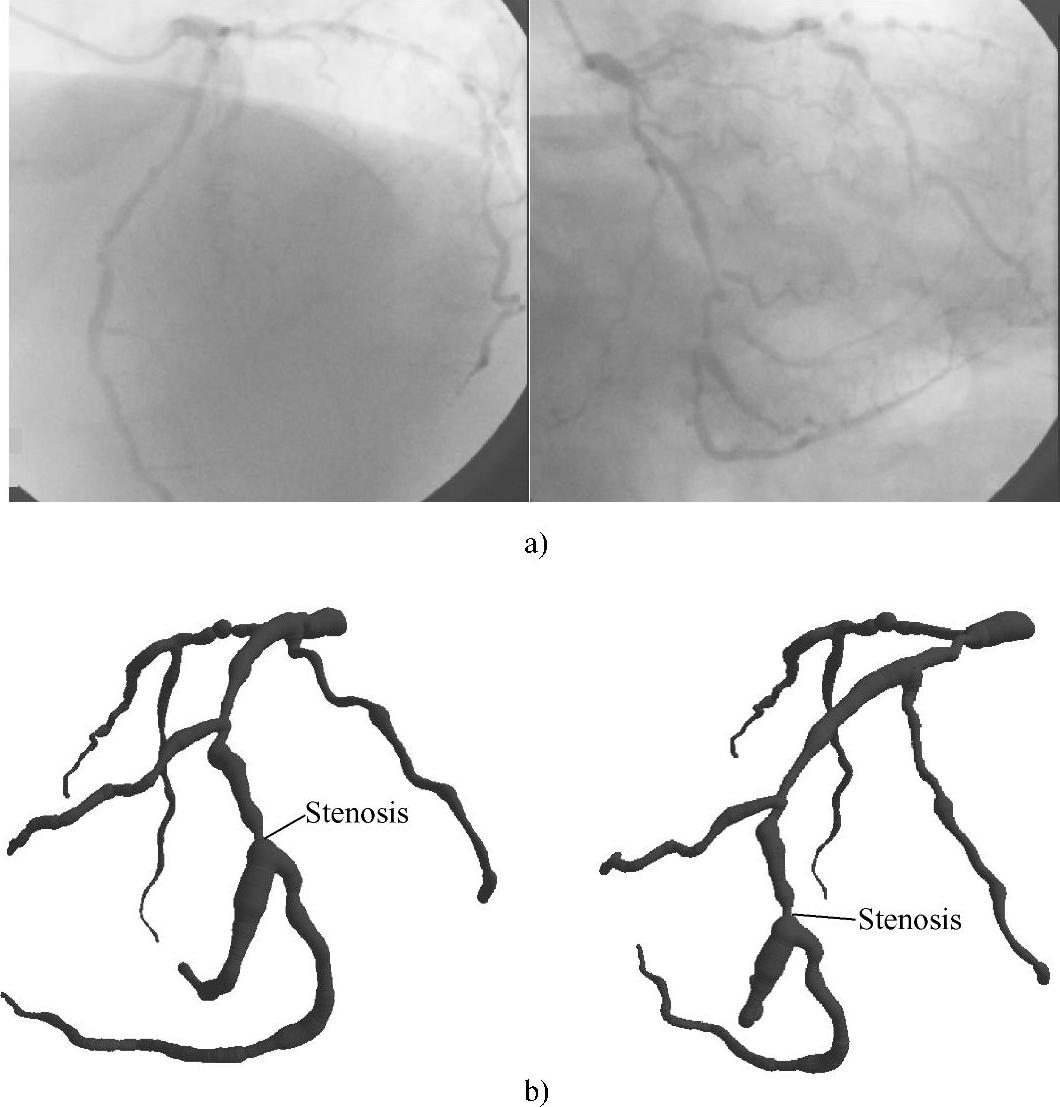
图2-52 对近似正交的一对左冠CAG图像进行血管三维重建的结果

a）造影角度分别为LAO50°CAUD8°和RAO30°CAUD14°的两幅左冠CAG图像 b）血管三维重建结果

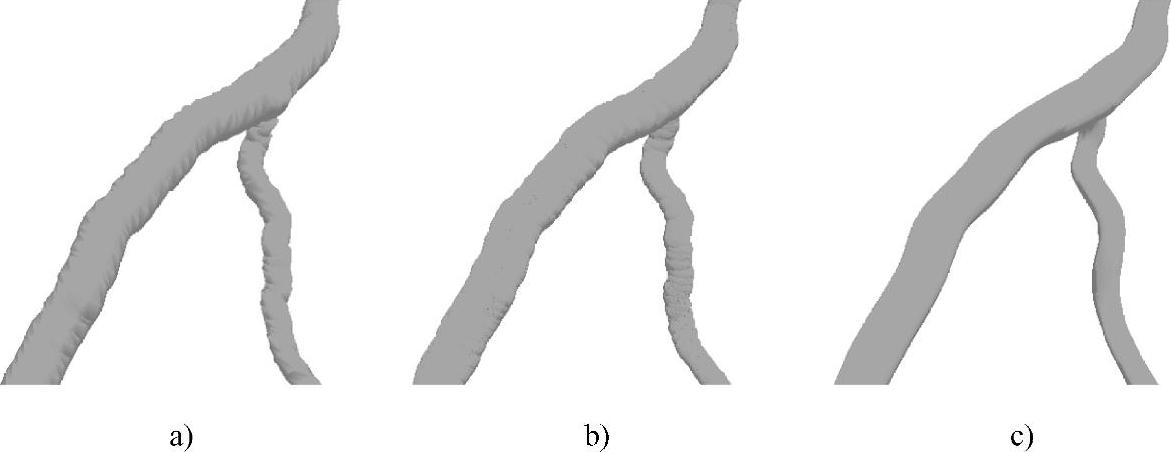
图2-53 三种血管表面重建方法实验结果的比较

a）球包络法 b）三角拼形接法 c）NURBS曲面拟合法

由于两个角度的投影数据有限，所以很难准确地重建血管的横截面。血管内超声或者血管内OCT图像可以准确展现血管横截面的形态，提供血管内部的形态和病变程度等重要诊疗信息，因此将重建得到的三维冠状动脉骨架和血管内超声或者血管内OCT图像提供的血管横截面信息相融合，可以得到病变血管的准确空间位置和形态，更好地辅助临床诊治，这也是冠状动脉三维重建技术的发展趋势。