视角对应点匹配优化策略

由两个不同角度的造影图像重建三维空间点时，一个关键问题是如何确定两幅造影图像的对应点，即匹配两幅图像的对应点，这是计算机立体视觉中常见的匹配问题。为了从二维图像中获得更多的三维信息，两幅造影图像A和B之间的造影角度一般应相差60°以上，因此两幅图像中几何结构的共性大大减少，无法使用常用的立体图像匹配技术（如模板匹配、关系匹配和特征内容匹配等）。目前常用的方法是利用立体成像的外极线约束匹配对应点。

从两个不同视角获得的同一场景的两幅图像之间存在着一定的约束关系，这就是通常所说的外极几何关系。如图2-30所示，空间点P与X射线源S₁和S₂构成一个平面，称为外极平面；外极平面与图像A和B相交形成左右两条外极线L₁和L₂。点P在图像A和B上的投影点分别为p₁和p₂，O₁和O₂分别是图像A和B的中心。根据透视投影成像原理和外极约束原理，点p₁在图像B上的对应点p₂一定位于点p₁对应的外极线L₂上，点p₂在图像A上的对应点p₁一定位于点p₂对应的外极线L₁上，这一性质称为匹配的外极线约束。

外极线是立体成像空间几何关系的体现，下面根据造影系统的几何变换矩阵GT推导外极线的方程。对两个造影成像平面上的点进行立体匹配时，首先在其中一个投影平面上取血管骨架点p，通过点p、S₁和S₂确定外极面，然后确定外极面与另一投影成像面的交线——外极线，最后在该外极线上寻找血管骨架点与p相匹配。如图2-27所示，空间点P在X射线源局部坐标系X₁Y₁Z₁S₁和X₂Y₂Z₂S₂中的坐标分别为（x₁，y₁，z₁）和（x₂，y₂，z₂），P在图像A上的投影点p₁的坐标为（u₁，v₁）（基于平面坐标系U₁V₁O₁），在图像B上的投影点p₂的坐标为（u₂，v₂）（基于坐标系U₂V₂O₂）。由式（2-20）可知：

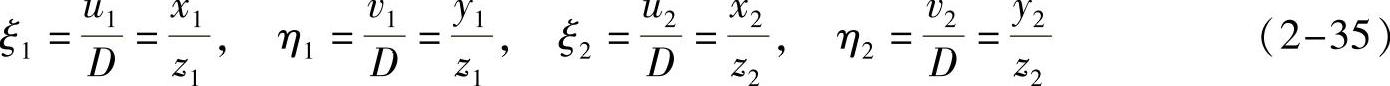
于是有如下公式：

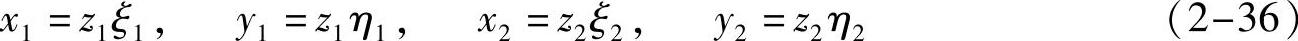
即：

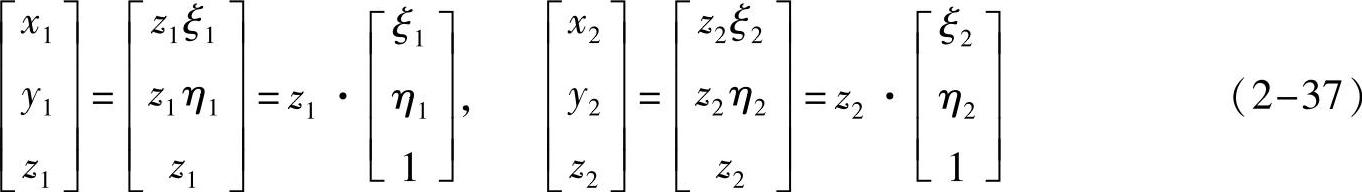
由式（2-26）有：

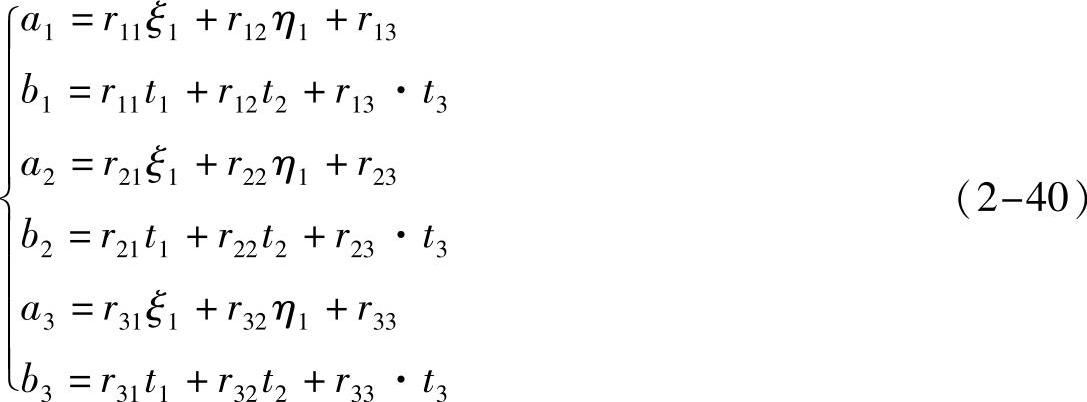
则式（2-39）可以写成：

所以：

(www.xing528.com)

从上式中消去z₁并化简，则图2-30中图像A上的点p₁（u₁，v₁）在图像B上对应的外极线L₂的方程可表示如下：

u₂（a₂b₃-a₃b₂）＋v₂（a₃b₁-a₁b₃）＋D₂（a₁b₂-a₂b₁）＝0 （2-43）

或

ξ₂（a₃b₂-a₂b₃）＋η₂（a₁b₃-a₃b₁）＋（a₂b₁-a₁b₂）＝0 （2-44）

同理，可推出外极线L₁的方程。

利用外极约束匹配血管骨架点如图2-31所示，图中三维血管V分别成像于图像A和图像B，图像A中的点p₁在图像B上对应的外极线为L₂。根据外极约束原理，点p₁在图像B上的对应点一定在外极线L₂上，且一定在图像B中的血管投影上。所以外极线L₂和图像B中血管投影的交点p₂就是点p₁的共轭点。

由于二维血管提取的误差以及几何变换矩阵的误差等，匹配点可能不会准确地出现在图像平面中对应的外极线上，而在外极线的邻域内。这种情况下，一般在该邻域内搜索和外极线距离最短的点作为匹配点。由解析几何知识以及式（2-44），可以计算图像B上的点（u₂，v₂）到外极线L₂的距离，公式如下：

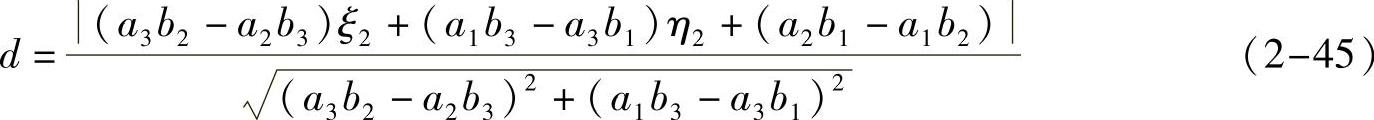
其中，a_i和b_i（i＝1，2，3）的值和式（2-41）中的值相同。则d可以作为点p₂相对于p₁的匹配误差。

另外，由于冠脉血管骨架成树状结构，外极线上可能存在多个血管骨架点，例如图2-30中的骨架点p′₁、p′₂和p′₃。如2.4.4节中所述，经过分割，可以用有向二叉树描述二维冠脉树骨架的拓扑结构，如图2-31所示，基于冠状动脉树骨架特有的树状拓扑结构，为提高匹配精度，可以利用血管树固定的层次关系作为匹配的主要特征，即仅允许具有相同拓扑特性的血管段进行匹配，从而缩小匹配的搜索范围，简化匹配过程，提高匹配精度。

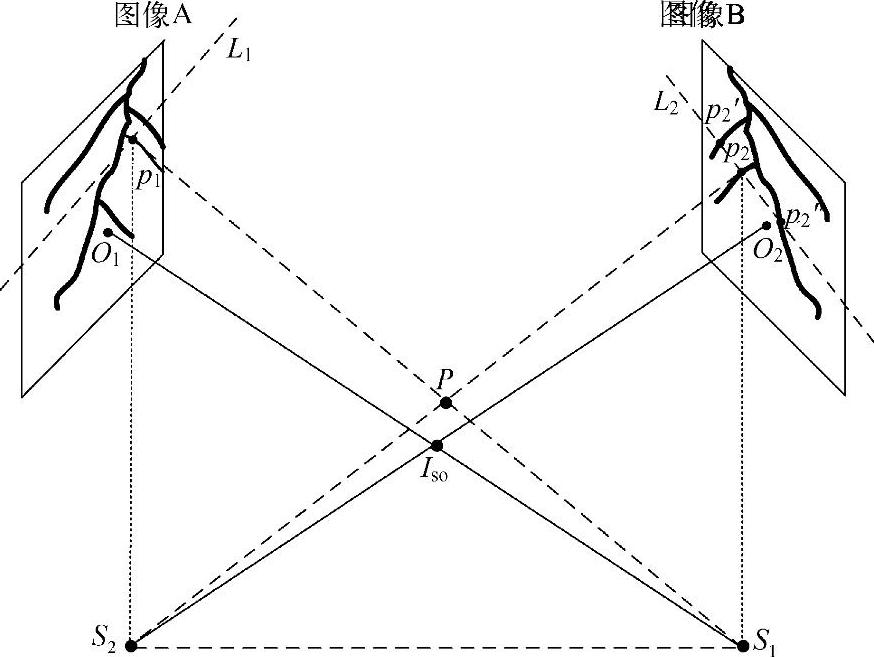
图2-30 外极几何关系示意图

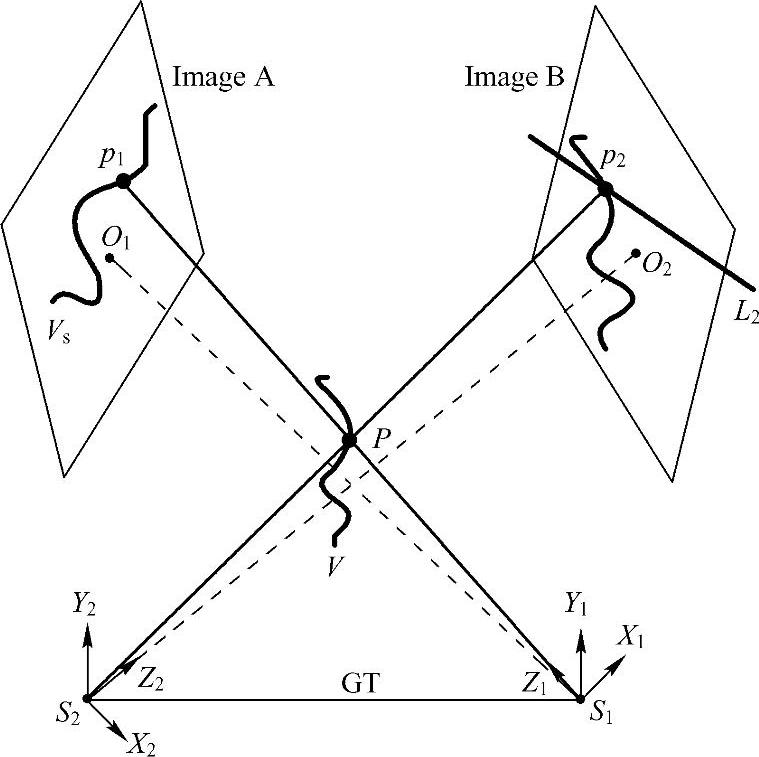
图2-31 利用外极约束匹配血管骨架点