造影成像系统的几何模型优化探讨

造影系统在两个不同角度的成像平面之间存在着一定的立体几何关系，这是由二维造影图像是重建三维血管的关键。本节根据造影系统的运动特征建立简化模型，分析造影图像平面和三维坐标系之间的几何转换关系，以及两个造影图像之间的几何转换关系。

单面造影机的运动模型如图2-24所示，造影机的旋转运动包括绕轴I的旋转I和绕轴II的旋转II，轴I和轴II的交点为系统中心；造影机的平移运动指图像增强器在桶架上的直线运动，另外病人躺卧的平台也会有平移运动。因此，造影系统具有五个自由度：两个旋转运动的角度、X射线源和图像增强器相对于系统中心点的平移矢量以及桶架的平移矢量（即图中轴I和轴II方向的运动矢量）。造影机的X射线源是一个接近于点，但具有一定面积的射线源。由于X射线源的尺寸远小于其与接收端之间的距离，同时为了研究方便，因此假设X射线源为一个理想的点源，它发射一个锥形的射线束，X射线投影轴垂直入射到成像平面，因此X射线造影可以看成简单的一点透视，X射线源也就是透视投影的灭点。根据透视投影原理，建立X射线造影系统的投影模型，如图2-24中简化的成像模型所示。

以系统中心为原点O，垂直于平台向上的方向为Z轴，X轴指向病人右手方向，Y轴指向病人脚的方向，建立如图2-25所示的右手三维笛卡尔坐标系（即世界坐标系），图2-24中造影机的旋转I和旋转II的旋转轴分别为Y轴和X轴。

造影角度记录了图像获取过程中造影机位置，是血管三维重建所需的重要参数，其定义详见2.2.3节。图2-26描述了造影机在两个不同角度投影时造影角度的表示方法，其中点S₁和S₂代表两次造影过程中X射线源的位置，坐标系XYZO是按如图2-25所示方法建立的坐标系，坐标系X₁Y₁Z₁S₁和X₂Y₂Z₂S₂分别是以点S₁和S₂为原点的X射线源局部坐标系，S₁O₁和S₂O₂分别是投影坐标系X₁Y₁Z₁S₁和X₂Y₂Z₂S₂的投影轴，分别垂直入射图像A和B于点O₁和点O₂。两次造影角度分别记为（α₁，β₁）和（α₂，β₂），α₁和α₂在XZO平面内，表示LAO／RAO角度，当α_i＞0时代表RAO角度，当α_i＜0时代表LAO角度；β₁和β₂分别在OO₁A₁和OO₂A₂平面内，表示CRAN／CAUD角度，当β_i＞0时代表CRAN角度，当β_i＜0时代表CAUD角度。所以图2-26中，α₁＜0、β₁＞0、α₂＞0和β₂＞0。这样在不同体位对冠脉进行造影成像时，坐标系X₁Y₁Z₁S₁和X₂Y₂Z₂S₂相对于坐标系OXYZ的旋转角度均可从造影机上得到。

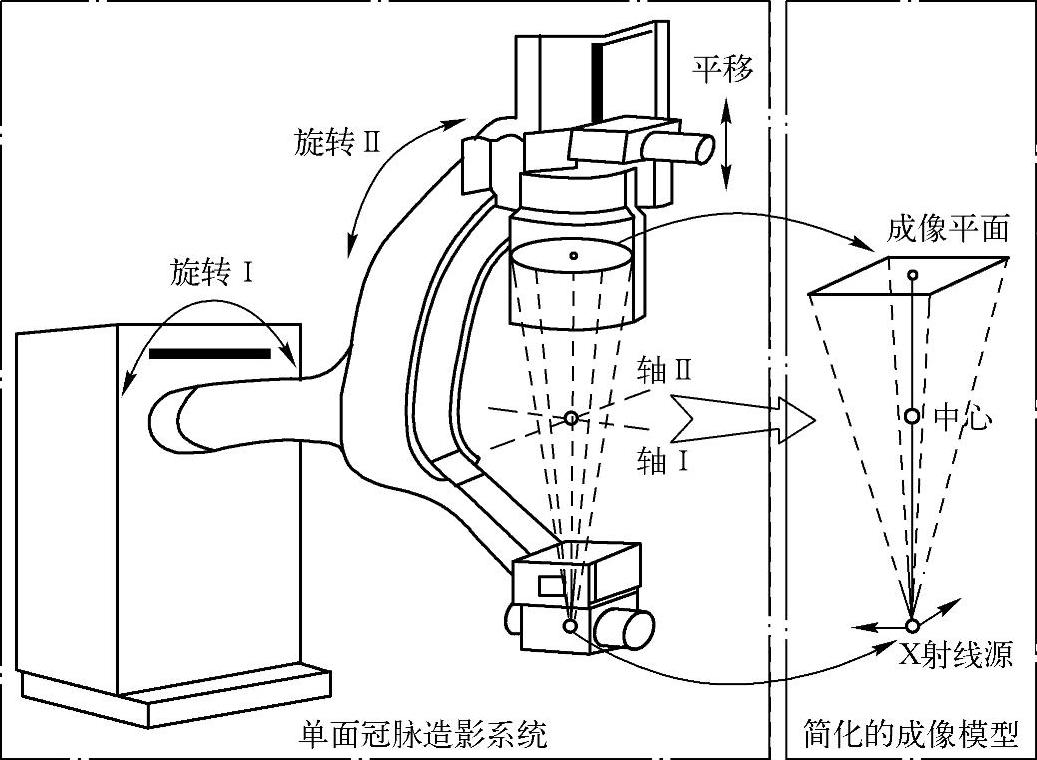
图2-24 单面造影机运动模型^［16］

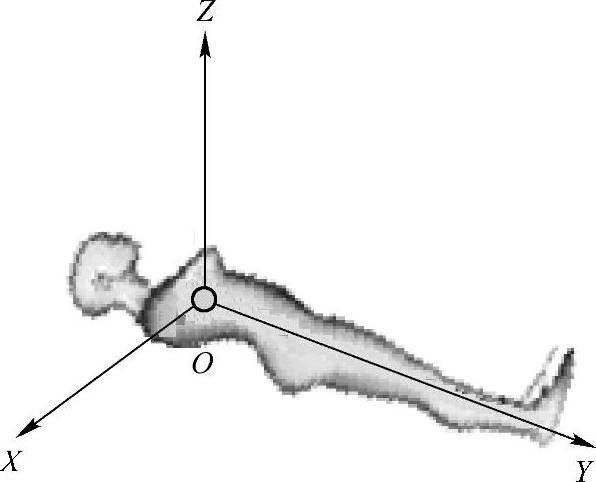
图2-25 右手三维笛卡尔坐标系

血管造影系统在两个不同角度的成像示意图如图2-27所示，投影面坐标系U₁V₁O₁和U₂V₂O₂所在平面分别代表两次造影过程中的图像平面，即图像A和图像B平面。D₁和D₂分别表示X射线源S₁和S₂到各自投影平面的垂直距离。坐标系U₁V₁O₁中，空间点P在图像A上的投影点p₁的坐标为（u₁，v₁）；坐标系U₂V₂O₂中，空间点P在图像B上的投影点p₂的坐标为（u₂，v₂）。利用两个不同角度的造影图像重建三维血管，也就是根据图像A和B上的对应点p₁和p₂，计算出空间点P的三维坐标。

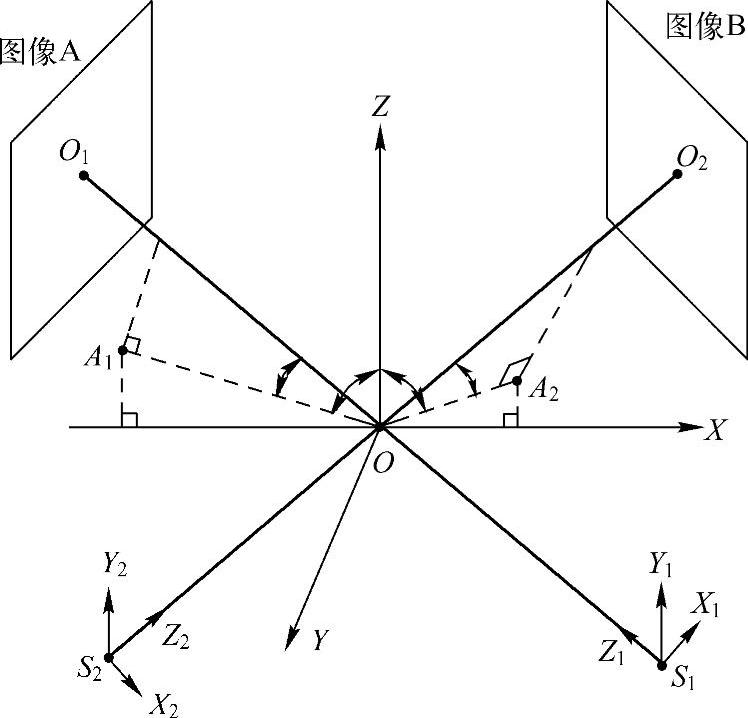
图2-26 造影角度的表示方法

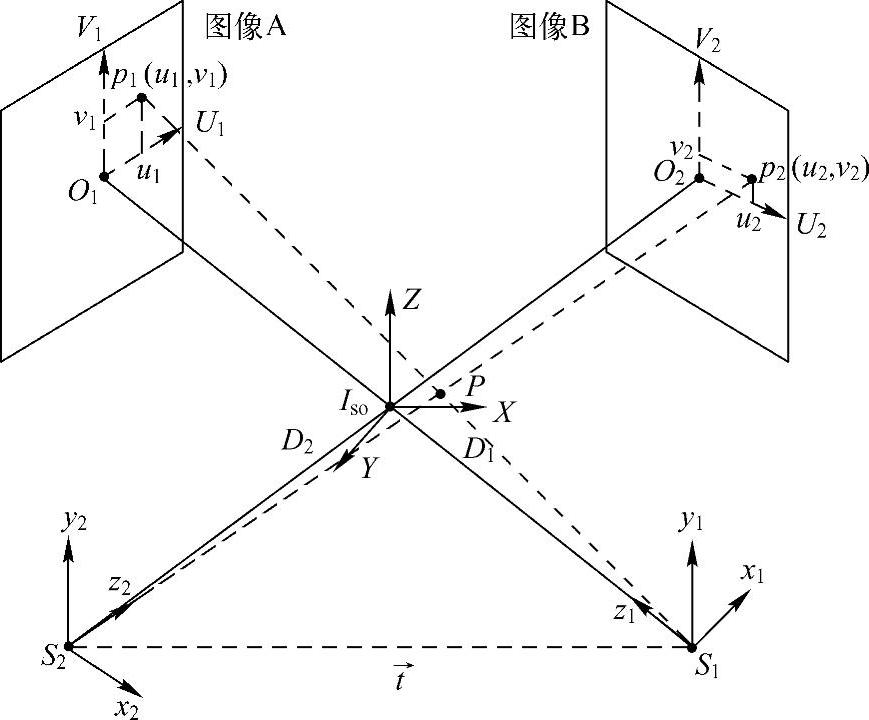
图2-27 造影系统在两个不同角度的成像示意图^［16］

综上所述，定义四个坐标系，分别为以系统中心O为原点的世界坐标系XYZO，如图2-25～2-27所示；以X射线源S_i（i＝1，2）为原点的X射线源局部坐标系X_iY_iZ_iS_i（i＝1，2），如图2-25和图2-26所示；以图像中心O_i为原点的投影面坐标系U_iV_iO_i（i＝1，2），如图2-27和图2-28a所示；以图像左上角I为原点的图像平面坐标系E_iF_iC_i（i＝1，2），如图2-28b所示。其中，世界坐标系、X射线源局部坐标系和投影面坐标系的坐标单位是mm，图像平面坐标系的坐标单位是像素。

根据投影面坐标系（或图像平面坐标系）上的两个对应点，计算世界坐标系（或X射线源局部坐标系）的三维点坐标，需要推导这四个坐标系之间的几何关系，如图2-29所示。下面仅介绍结论，详细推导过程参见文献［10，16，36～39］。

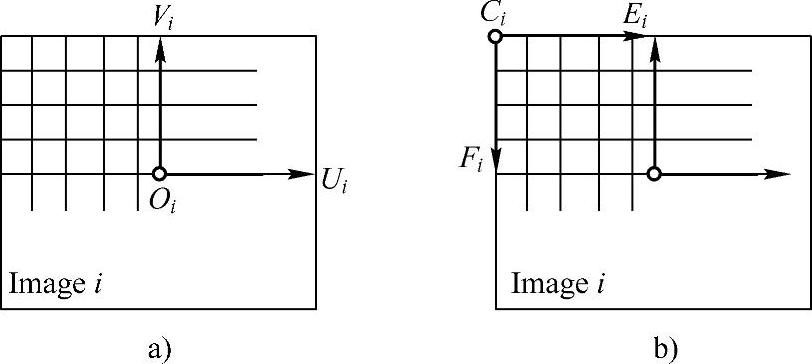
图2-28 以图像左上角I为原点的图像平面坐标系

a）投影面坐标系 b）图像平面坐标系

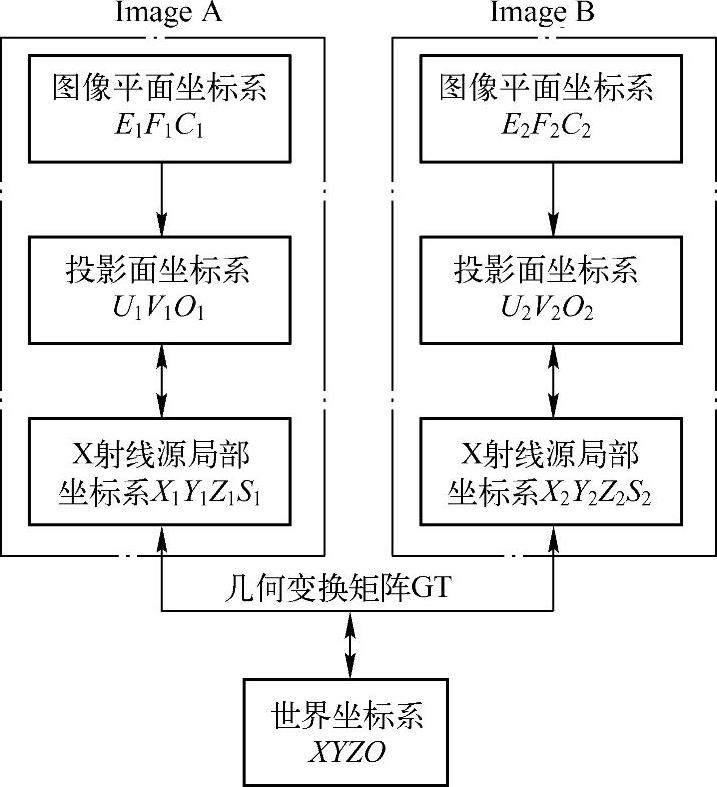
图2-29 四个坐标系几何关系

（1）图像平面坐标系和投影面坐标系的转换关系

投影面坐标系U_iV_iO_i和图像平面坐标系E_iF_iC_i（i＝1，2）都是建立在造影图像平面上的坐标系，如图2-28所示，二者的坐标值可以用造影图像的像素间距q进行换算。像素间距指图像上相邻像素的间隔距离，单位是mm／pixel，临床一般选用的值为0.3mm／pixel或0.35mm／pixel。设图像i的大小为W×H（像素），则图2-28a中的坐标系原点O_i在图2-28b坐标系中的坐标为（W／2，H／2）。于是坐标系U_iV_iO_i中一点的坐标（u_i，v_i）和坐标系E_iF_iC_i中的坐标（e_i，f_i）之间的转换关系如下：

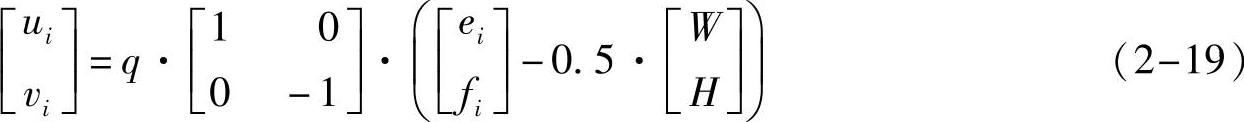
（2）投影面坐标系和X射线源局部坐标系的转换关系

投影面坐标系U_iV_iO_i与X射线源局部坐标系X_iY_iZ_iS_i（i＝1，2）的关系如图2-27所示，X_iS_i和Y_iS_i轴分别平行于U_iO_i和V_iO_i轴，S_iZ_i轴垂直于图像平面，S_i和O_i之间的距离为D_i（i＝1，2）。根据透视投影原理，可以推导出坐标系U_iV_iO_i中一点的坐标（u_i，v_i）和坐标系X_iY_iZ_iS_i中的坐标（x_i，y_i，z_i）之间的转换关系如下：

（3）X射线源局部坐标系和世界坐标系的转换关系

在图2-26中，从世界坐标系XYZO到X射线源局部坐标系X_iY_iZ_iS_i（i＝1，2）的几何变换是三维空间的刚体运动，可以用旋转和平移运动描述。设点S_i和点O之间的距离为L_i，可以通过两次旋转变换和一次平移变换实现由XYZO到X_iY_iZ_iS_i的转换具体为绕Y轴顺时针旋转α_i角度；绕X轴顺时针旋转β_i角度；从O点平移L_i距离到S_i点。推导可得坐标系XYZO中一点的坐标（X，Y，Z）和坐标系X_iY_iZ_iS_i中的坐标（x_i，y_i，z_i）之间的转换关系如下：［x_i，y_i，z_i，1］＝［X，Y，Z，1］·R_Y（α_i）·R_X（β_i）·T_i(www.xing528.com)

式中，矩阵R_X（θ）表示绕X轴顺时针旋转θ角度的旋转矩阵；R_Y（θ）表示绕Y轴顺时针旋转θ角度的旋转矩阵；T_i表示沿Z轴平移L_i的平移矩阵。通过矩阵变换，可以将式（2-21）表示为

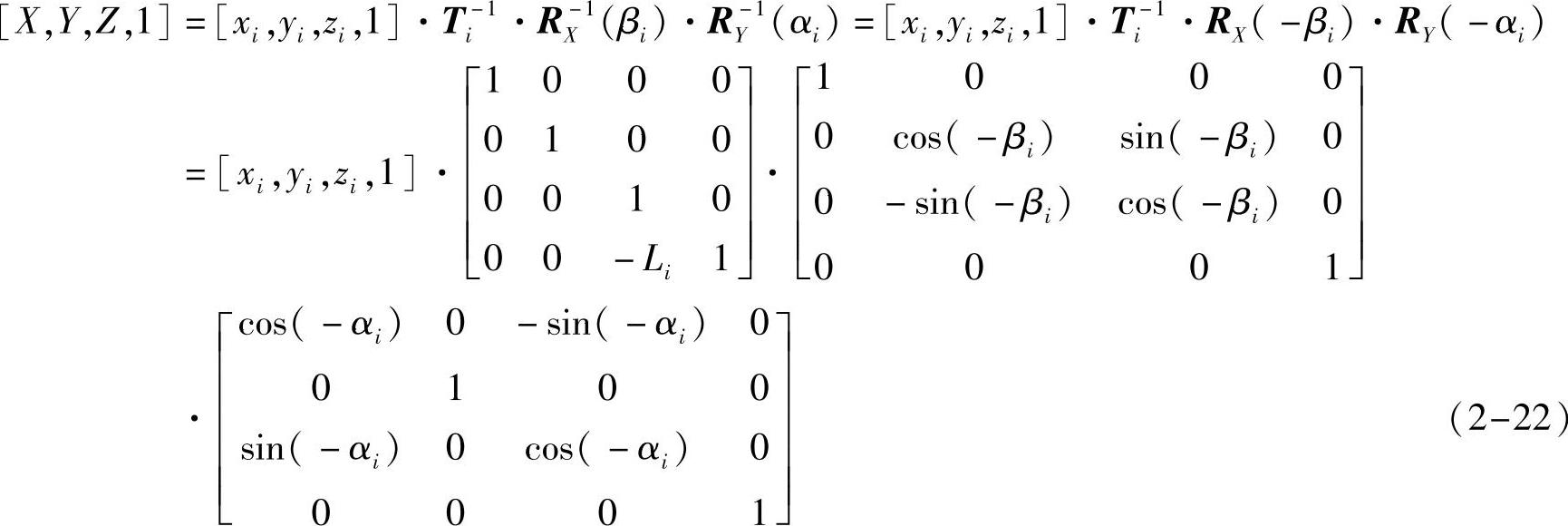
式中，T^-1和R^-1分别表示矩阵T和R的逆矩阵。

（4）两个X射线源局部坐标系之间的转换关系

坐标系X₁Y₁Z₁S₁和X₂Y₂Z₂S₂之间的转换关系可以通过中间坐标系XYZO推导得到。坐标系X₁Y₁Z₁S₁中一点的坐标（x₁,y₁，z₁）与坐标系XYZO中的坐标（X，Y，Z）之间的转换关系如下：

式中，L₁为X射线源S₁和系统中心O之间的距离；T₁为沿Z轴平移L₁的平移矩阵。为了方便描述矩阵变换，上式中采用齐次坐标［x₁，y₁，z₁，1］和［X，Y，Z，1］分别表示坐标（x₁，y₁，z₁）和（X，Y，Z），下同。

坐标系X₂Y₂Z₂S₂中一点的坐标（x₂，y₂，z₂）与坐标系XYZO中的坐标（X，Y，Z）之间的转换关系如下

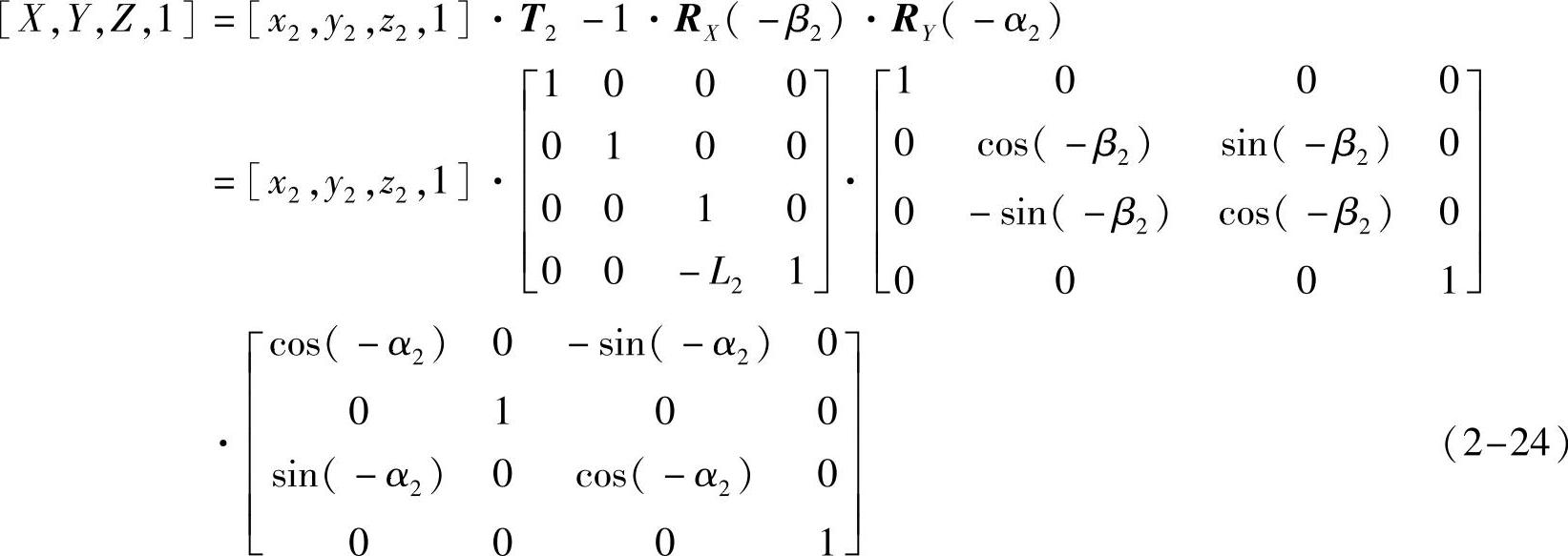
式中，L₂为X射线源S₂和系统中心O之间的距离；T₂为沿Z轴平移L₂的平移矩阵。

联立式（2-23）和式（2-24）可得坐标系X₁Y₁Z₁S₁和X₂Y₂Z₂S₂之间的几何变换关系，公式如下：

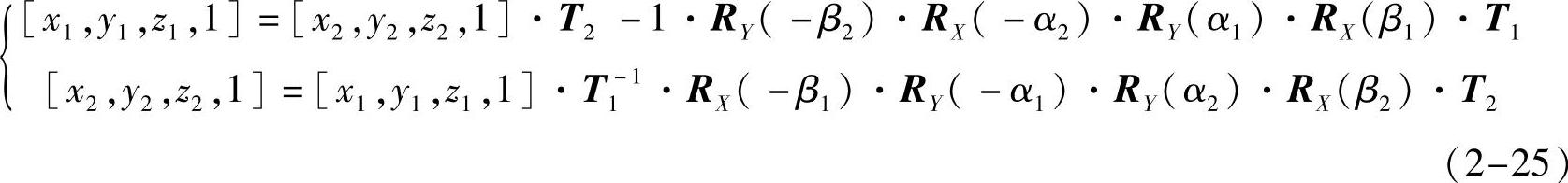
将式（2-25）用非齐次坐标表示为

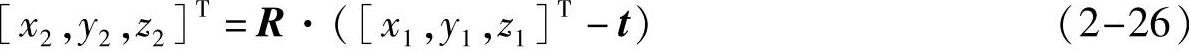
其中R为33的旋转矩阵，其公式如下：

R＝R_X（β₂）·R_Y（α₂）·R_Y（-α₁）·R_X（-β₁） （2-27）

t为3×1的平移矢量，其公式如下：

t＝T₁-R^-1.T₂＝T₁-R_X（β₁）·R_Y（α₁）·R_Y（-α₂）·R_X（-β₂）·T₂（2-28）

所以坐标系X₁Y₁Z₁S₁和X₂Y₂Z₂S₂之间的几何变换关系可以用旋转矩阵R和平移矢量t表示。定义3×4的矩阵如下：

GT＝［Rt］ （2-29）

称为几何变换矩阵，它记录了两次造影时成像系统的几何位置关系，是联系两个不同角度造影图像的纽带，也是三维重建血管的关键。

上述坐标变换仅考虑了坐标系本身的运动，忽略了图像获取过程中病人的位置变化，即病人的平移运动。为了获得更多的信息和观察方便，造影过程中操作人员常常会移动病人躺卧的平台，所以两次造影时平台一般不在同一位置。设

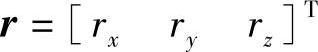
为造影成像过程中病人的平移运动，当重建过程考虑运动r以后，式（2-26）变成：

坐标系X₁Y₁Z₁S₁和X₂Y₂Z₂S₂之间的几何变换关系可以用式（2-26）或（2-30）表示，这也是计算三维血管坐标的必要条件。根据L₁、L₂和造影角度可以计算几何变换矩阵GT，但由于在对成像系统进行标定，获得这些参数时不可避免地存在一定误差，所以GT不能很好地反映两幅造影图像之间的几何变换关系，从而影响血管三维重建的精度。一般选择两幅造影图像的特征点对（如分叉点等）优化GT，从而提高三维重建的精度，详见文献［10］。