弹性与胡克常数：理解与应用

弹性是物体在外力作用下改变其形状和大小而外力卸载后可回复原始形状和大小的性能。1678年胡克发现了弹性定律，给弹性力学和弹性测量学打下了基础。胡克定律是力学基本定律之一，是适用于一切固体材料的弹性定律，其内容可简单表述为：在弹性限度内，物体的形变与引起形变的外力成正比。

胡克弹性定律也可表述为：在应力低于比例极限的情况下，固体中的应力σ与应变ε成正比，即：σ=Eε （9-1）

式中 σ——应力，单位为N/mm²；

E——弹性模量，单位为N/mm²；

ε——应变。

把胡克定律推广应用于三向应力和应变状态，则可得到广义胡克定律。分析物体受力情况时，在所考察的那—点附近取一个足够小的立方体。一般用三个应力来描述周围力对小立方体的作用。其中，方向与立方体表面垂直的称为正应力，与表面平行的称为切应力。应力的脚标中，第一个字母表示应力作用在哪个面上，第二个字母表示应力作用的方向。为了描写物体内某点处的应力状态，只需σ_xx、σ_yy、σ_zz、σ_yz、σ_zx和σ_xy这六个独立的应力分量即可，而相对应有六个独立的应变ε_xx、ε_yy、ε_zz、ε_yz、ε_zx和ε_xy，因此，物体中任意一点的六个应力分量中的每一个都是六个应变分量的线性函数；反过来，应变分量也是应力分量的线性函数。各向同性材料的广义胡克定律有两种常用的数学形式如下：

应力与应变间的关系是：

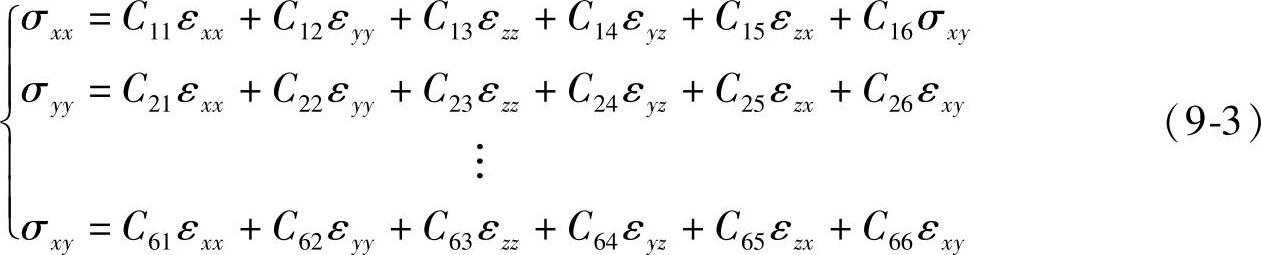
在公式（9-3）中形成的6×6矩阵的36个C_ij被称为弹性劲度系数，而公式（9-2）中的36个S_ij被称为弹性柔度系数，这两个矩阵之间是互为转置的。由于S矩阵与C矩阵具有对称性，独立的系数不是36个，而是21个。随着晶体对称性的提高，独立的弹性劲度系数C_ij或弹性柔度系数S_ij数目越来越少。对应晶系独立的劲度系数或柔度系数的个数如下表9-1所示。(www.xing528.com)

表9-1 对应晶系独立的劲度系数或柔度系数的个数

对于多晶体构成的金属材料，一般具有各向同性的特征，此时胡克定律为：

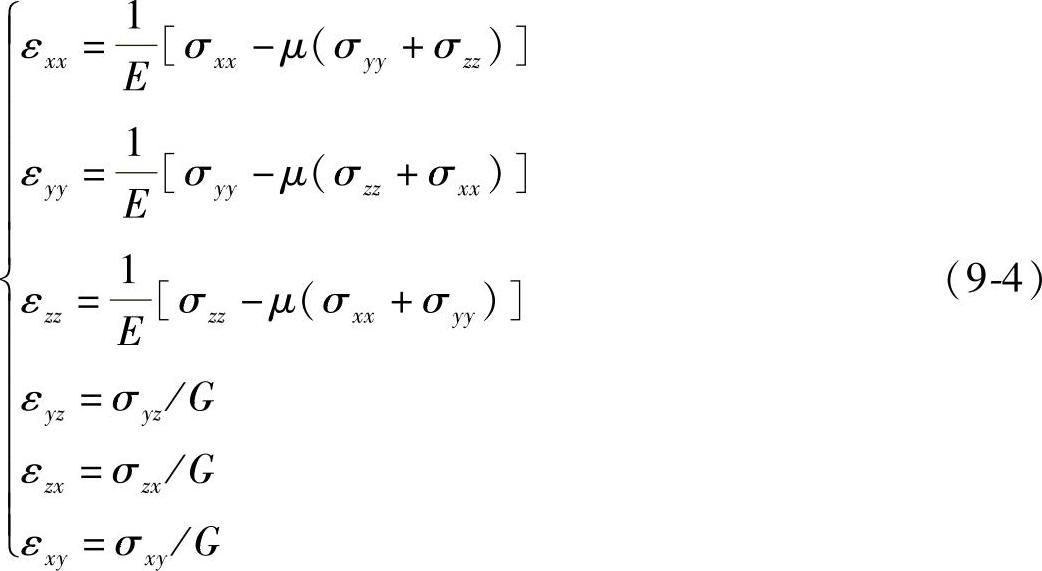
式中 ε_ij——法向为i的面元j方向上的应变；

σ_ij——法向为i的面元j方向上的应力，单位为N/mm²；

E——物体弹性模量，单位为N/mm²；

G——物体切变模量，单位为N/mm²；

μ——泊松比。