食品TTT概念与货架期监控

（一）食品的TTT（Time⁃Temperature Tolerance）

TTT理论是美国Arsdel等人于1948年到1958年在所做大量实验的基础上，总结出的为保持冷冻食品的优良品质所容许的贮藏时间和品温之间的关系。其主要内容见下文。

1.冷冻食品在流通过程中的品质变化主要取决于温度 冷冻食品的品温越低，其优良品质的保持时间越长。大多数冷冻食品的品质稳定性随食品温度的降低而呈指数关系地增大。在-30～-10℃的冷藏温度范围内，冷冻食品的贮藏温度与实用冷藏期之间的关系，基本上是呈倾斜的直线形状，这样的曲线叫TTT曲线，见图7⁃3。根据TTT曲线的斜率可知道贮藏温度对冷冻食品品质的影响，用温度系数Q₁₀表示。在-25～-15℃的实用冷藏温度范围内，Q₁₀的值为2～5。

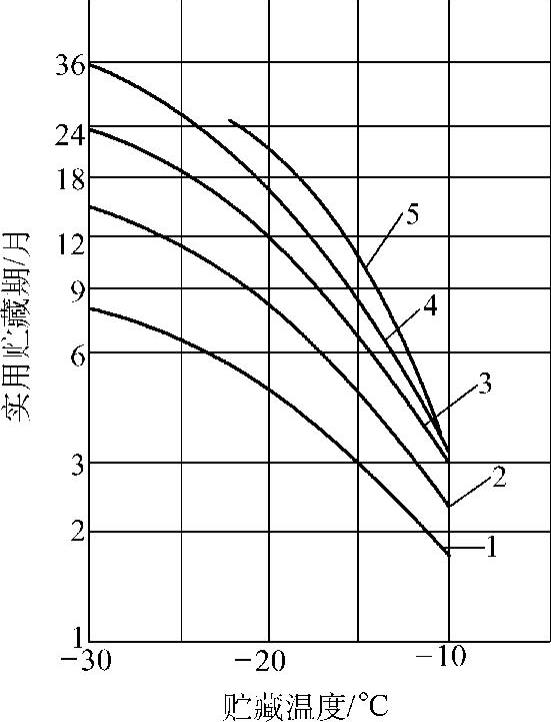
图7⁃3 冷冻食品的TTT曲线

2.时间⁃温度的经历对品质的影响冷冻食品在贮藏、运输、销售等流通环节中，因时间⁃温度的经历而引起的品质降低量是累积的、不可逆的，但与所经历的顺序无关。例如把相同的冷冻食品分别放在两种场合进行贮藏：一种是开始放在-10℃贮藏1个月，然后放在-25℃贮藏4个月；另一种是开始放在-25℃贮藏4个月，然后放在-100℃贮藏1个月，这两种场合分别贮藏5个月后，其品质下降量是相等的。

3.对于大多数冷冻食品来说，-18℃是最经济的贮藏温度 冷冻食品从生产出来到消费者手上，经历了贮藏、运输、批发、零售店冷藏、冷冻陈列柜销售等各个环节。从TTT理论可知，冷冻食品在流通过程中的品质变化主要取决于温度。为了使生产出来的优质冷冻食品的优良品质能一直持续到消费者手上，必须把从生产者到消费者之间流通的所有环节都维持低的品温，通过冷藏设施，用低温的链把各个环节连接起来。运输环节可看作是冻结贮藏的延长，需要普及低温运输的冷藏火车、冷藏汽车及冷藏船等设施。这种从生产到消费之间的连续低温处理叫冷藏链，由于欧美等发达国家实施和完善了冷藏链，使冷冻食品生产出来后，品温一直可以维持在-18℃以下，其优良品质得到很好的保持。冷冻食品的消费量逐年上升，有些食品如法式油炸土豆条、比萨饼等，还在国际范围内得到流通。我国在上海、北京等大城市中，随着冷冻食品消费量的增加，冷藏链的设施也正在逐步建立和完善。

4.利用TTT线图对冷冻食品在流通过程中的品质变化进行计算 冷冻食品从生产出来直到消费者手上，如果品温能保持在-18℃以下，并能稳定不变，这对冷冻食品优良品质的保持是十分理想的。但是在实际的贮藏、运输、销售等流通过程的各个环节中，温度经常会上下波动，这对冷冻食品的品质会带来很大影响。因此知道冷冻食品在流通过程中的品质变化，在实用上就显得十分重要。我们把某个冷冻食品在流通过程中所经历的温度和时间记录下来，可利用TTT线图进行品质变化的计算。

根据TTT曲线可知道，一个冷冻食品在某个温度的实用冷藏期是A，也就是这个冷冻食品原来的品质是100%，经过时间A后其品质下降到0，那么在此温度下，该冷冻食品每天的品质降低量为B=100/A，根据这个关系可作出它的品质保持特性曲线B。TTT线图就是在这个基础上做成的。其示例图7⁃4所示是利用TTT线图进行计算的一例。

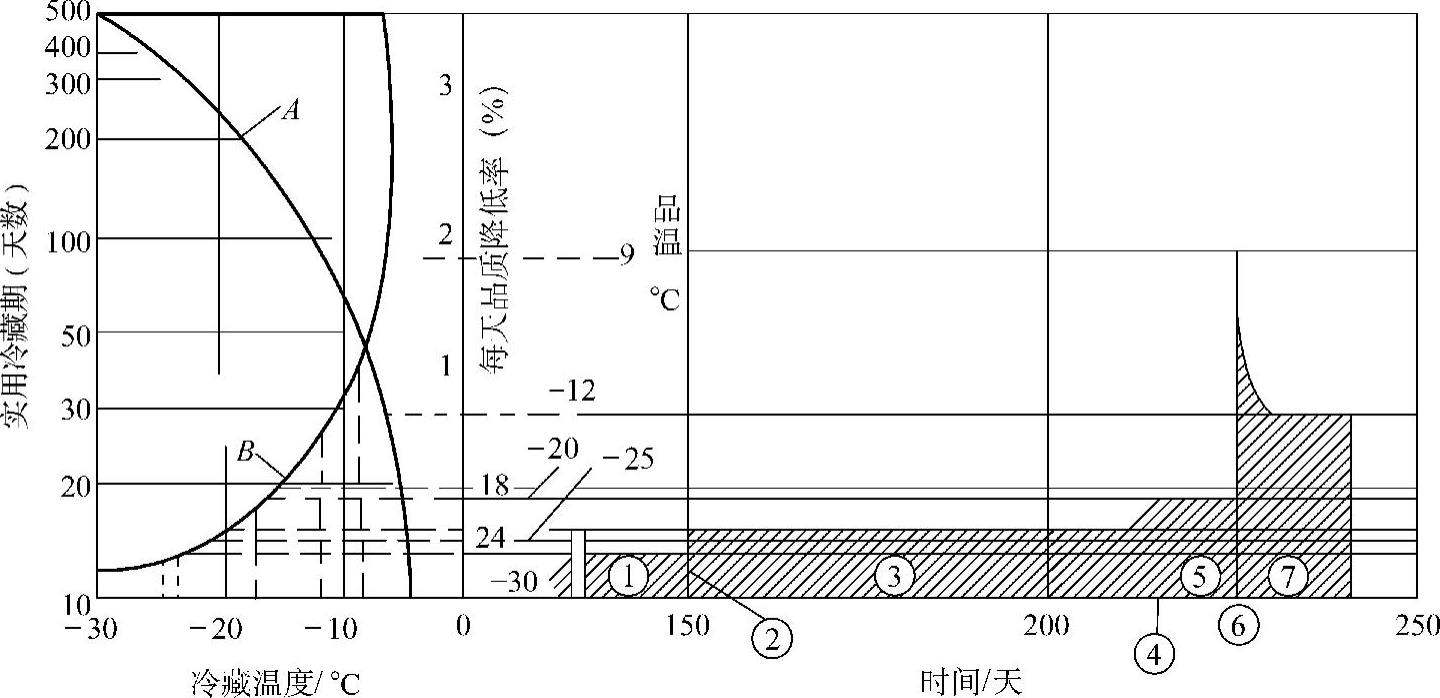
图7⁃4 TTT线图一例

1—多脂肪鱼（鲑）和炸仔鸡 2—少脂肪鱼 3—四季豆和汤菜 4—青豆和草莓 5—木莓

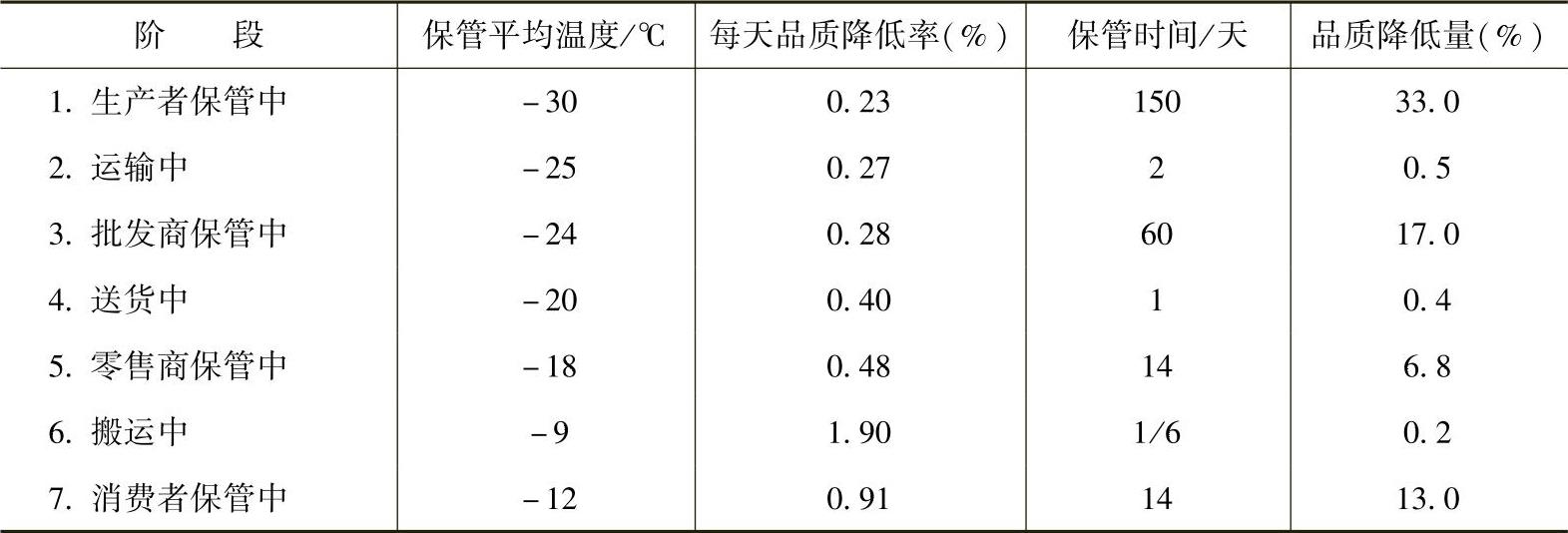
图7⁃4中，横坐标是天数，纵坐标是各种温度下的品质降低率（用百分数表示）。我们把某冷冻食品从生产出来一直到消费者手上所经历的贮藏、运输、销售等环节的温度、时间画在图上，这曲线下的面积就是该冷冻食品在流通过程中品质降低的总量。品温变化越大，曲线下的面积也越大，品质降低的量也越大。例如有一个冷冻食品，从生产到消费共经历了7个阶段，如表7⁃5所示。可用TTT的计算方法，根据各个温度下每天的品质降低率，与在此温度下所经历的天数相乘，即可算出某冷冻食品各个阶段的品质降低量。刚生产出来时，该冷冻食品的冷藏性为100%，从生产者到消费者共经历了214天，七个阶段的品质降低总量为70.9%，这说明该冷冻食品还有30%的剩余冷藏性。当品质降低总量超过100%时，说明该冷冻食品已失去商品价值，不能再食用了。

表7⁃5 某冷冻食品流通过程中温度、时间经历一例

目前TTT理论的应用已经从冷冻食品货架期的预测拓展到了冷藏食品。

（二）货架期的监控

1975年，Gacula等人将工程产品失效的概念引入食品领域。认为食品品质随着时间的推移不断下降，并最终降低到人们不能接受的程度，这种情况称为食品失效（Food Failure），失效时间则对应着食品的货架寿命。食品的货架寿命是指从感官和食用安全的角度分析，食品品质保持在消费者可接受程度下的贮藏时间。食品的货架寿命主要取决于四个因素：组成结构，加工条件，包装，贮藏条件。

对易腐、需低温保存食品而言，食品从生产到分配、贮藏和消费的整个过程中，食品的品质和它的货架期在很大程度上取决于它的实际温度历程，因此在低温流通过程中进行温度监控是非常有必要的。例如，通常在4℃的低温条件冷却肉的保质期约为5天，而在37℃或更高的温度下保存则不过几个小时。但由于食品在整个贮存⁃运输⁃销售过程温度变化的不可预测性，使得食品标注的货架期与食品真正可流通期限很难一致，仅标明食品使用期限难以保证食品品质，从而造成浪费。因此有关食品货架期模型的研究是目前研究的热点问题之一。

尽管不同食品腐败的机理各不相同，且变质反应非常复杂，但通过对变质机理的研究，能找到预测食品货架寿命的方法，食品腐败过程中品质的损失可以通过动力学模型得到很好的反映。化学反应动力学模型是反映食品品质变化基础的理论模型，可根据在不同条件下，对食品品质分析推导出一系列的预测模型，如基于食品色泽变化来测定食品品质损失程度的亮度法（L^∗），可预测杀菌操作中食品货架寿命的Z值模型，根据食品中特定微生物SSO生长来预测易腐食品货架寿命的微生物动力学生长的数学模型。另外，也可以通过对化学反应动力学模型进行推导而获得货架期寿命预测模型，如Q₁₀是以Arrhenius关系式为基础推导出的预测模型。

1.食品品质函数 Labuza指出，在食品加工和贮藏过程中，大多数与食品质量有关的品质变化都遵循零级或一级反应动力学规律。针对不同的反应级数有不同的食品品质函数表达式（见表7⁃6）。大多数食品的质量损失可以用可定量品质指标A（如营养素或特征风味）的损失或感官品质指标B（异味或褪色的形成）来表示。

式中 k和k′——反应速率常数；

n和n′——反应级数。

表7⁃6 不同反应级数的食品品质函数的形式

A或B经过适当转换后可表示为时间t的线性函数。对零级反应采用线性坐标可得到一条直线；对一级反应采用半对数坐标也能得到一条直线；这样，根据少数几个测定值和线性拟合的方法就可求得上述级数，并求得品质函数F（A）中各参数的值。然后通过外推求得货架寿命终端时间的品质A（或B），也可计算出品质达到某一特定值时的贮藏时间。同样，也可求得某个贮藏时间的品质值。

食品品质函数的确立就可以在一定程度上解决同一种食品不同个体间品质变化的不可比较性，量化数据k（反应速率常数）就可对不同食品品质进行客观比较。而反应速率常数与温度的关系一般符合Arrhenius方程。

2.Arrhenius方程 食品因种类不同及所处环境条件的变化，使得描述某种食品货架寿命的动力学方程也随之变化。食品从工厂生产出来并包装好后，经过运输到仓库、批发中心、零售商，最后到消费者手里的全过程中，温度相对于诸如相对湿度、包装内的气体分压、光和机械力等一些因素，对食品质量损失的影响是居首位的，而且是唯一不受食品包装类型影响的因素。

Labuza应用Arrhenius关系式研究了食品的腐败变质速率。

式中 k₀——指前因子（又称频率因子）；

E_A——活化能（品质因子A或B变坏或形成所需克服的能垒）；

T——热力学温度（K）；

R——气体常数，1.9872cal/（mol·K）或8.3144J/（mol·K）。

k₀和E_A都是与反应系统物质本性有关的经验常数。

对式（7⁃3）取对数：

在求得不同温度下的速率常数后，用lnk对热力学温度的倒数（1/T）作图可得到一条斜率为-E_A/R的直线。Arrhenius关系式的主要价值在于：可以在高温（1/T）下借助货架期加速实验获得数据，然后用外推法求得在较低温度下的货架寿命。

3.亮度的变化测定质量损失法 食品的一些特别属性变化通常可以反映食品品质的损失。例如，某些食品可以通过亮度法（L^∗）来测定食品品质的损失程度。食品的亮度（L^∗）随着时间的变化可以表示为

式中 n——反应级数；(www.xing528.com)

k_brown——食品褐变速率常数，其取决于温度的变化T（K），且符合Arrhenius方程：

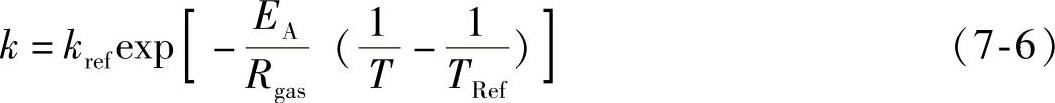
式中 k_ref——在参考温度下的速率常数；

E_A——反应的活化能（J/mol），活化能的变化反映着食品品质的损失程度；

R_gas——气体常数（8.314J/mol·K）；

T_Ref——参考温度（K）。

食品亮度的数学模型与反应级数有着密切的关系，由此模型所绘制的指数衰减曲线呈现出一种线性关系，从而由此曲线反映食品品质变化的程度。

4.Z值模型法 从反映温度对反应速率常数的影响的角度，除了Arrhenius模型外，还有就是Z值模型。对以化学反应为主的品质变化，如贮存、加热等过程，常用Arrhenius模型；对杀菌等操作，即以微生物改变为主的过程，常用Z值模型，用以评估食品品质损失。

食品工业中微生物的死亡大多应用一级反应动力学模型：

式中 N——t时的活菌数；

N₀——初始活菌数；

t——时间（s）；

D——10倍减少时间（Decimal Reduction Time）。

上式的物理意义可由（7⁃7）式变化后获知

即在一定环境和一定温度下杀死90%微生物所需的时间。D值越大，则该菌的耐热性越强。Z值定义为引起D值变化10倍所需改变的温度（℃），其定义式为

式中 D_r——参考温度下的D值，Z值越大，因温度上升而获得的杀菌效果增长率就越小。

由（7⁃8）式和（7⁃9）式组成Z值模型。

C.voegel—Turenp以类似于“热力-致死”的杀菌模型为基础，建立了三个经验模型以确定静态条件下，温度以及水分活度对苹果褐变反应诱导期长短的影响。

一般认为Arrhenius模型与Z值模型两者既有联系又有区别，在一定条件下的某一温度范围内，两者都可以表示为生物或营养物的耐热特性。由于模型本身的特点，外推实验温度时Z值模型所求得的k值恒高于Arrhenius模型的k值，在选择数学模型来描述食品品质损失时，需要对同样的实验数据用不同模型进行拟合，相互比较，方可确定哪一种模型更为合理。

5.Q₁₀模型 Q₁₀定义为温度上升10℃后，反应速率为原来速率的多少倍，或者指食品贮存在高于原来贮存温度10℃的条件下，其货架Q_S的变化率。Q₁₀的函数形式如下：

式中 θ_s——货架寿命（天）；

T₀——通过感官评定确定货架寿命的已知温度点（℃）；

T——所要求货架寿命的温度点（℃），T₀>T。

已知Arrhenius方程（7⁃3），对其进行微分，然后从T₁到T₂积分得到E_A与温度、反应速率常数的关系式：

式中 k₁、k₂——对应T₁、T₂温度下的速率常数。由回归计算可得出相差10℃时的活化能E_A。

由式（7⁃11）求得的E_A，而获得反映Q₁₀与活化能之间关系的模型：

式中 E_A——活化能（品质因子A或B变坏或形成所需克服的能垒）；

R——气体常数，8.3144J/（mol·K）。由式（7⁃12）可获得不同温度下的货架寿命。

6.描述微生物动力学生长的数学模型 食品腐败主要是微生物活动的结果。前人对食品的微生物腐败进行了大量系统的研究，特别是对水产品中微生物生长的预测研究，因为新鲜鱼类是最易腐败的一类食品。近年来食品微生物预报技术在国外被广泛研究，利用数学模型定量描述食品特性（如pH值、水分活度）和加工流通环境因子（如温度、气体组成）对食品中微生物生长、残存、死亡的动态影响，以预测货架寿命和微生物学安全性。对鲜鱼类腐败微生物研究的结果表明，在大多数情况下，鲜鱼类所含微生物中只有部分微生物参与腐败过程，这些适合生存和繁殖并产生腐败臭味和异味代谢产物的微生物，就是该产品的特定腐败菌（Specific Spoilage Organisms，SSO）。由于是SSO造成腐败，所以SSO的对数和产品剩余货架期之间存在密切关系，这就有可能依据SSO初始数和生长模型来预测产品的剩余货架期。近年来，研究者提出不少描述微生物动力学生长的数学方程，包括Logistic方程、Gompertz方程、Richards方程、Stannard方程、Schnute方程等，其中Logistic方程和Gompertz方程因使用方便，在有关SSO和腐败细菌生长动力学研究的文献中被广泛使用。

对多种水产品而言，货架期预测的核心是确定SSO并建立其相应的生长模型。在此基础上，通过预测SSO的生长趋势就可以成功预测产品的货架期。某一产品中，SSO达到稳定期后的最大菌数（N_max）和微生物在货架期终点时的菌数（N_s）基本固定在一个范围内，当N_max和N_s确定后，由Arrhenius模型可计算出最大生长速率（μ_max）与延滞时间（Lag），然后根据SSO生长动力学模型计算SSO从N₀增殖到N_s的时间，从而预测货架期（SL）。同样，根据Logistic方程或Gompertz方程，只要得到任何时刻的细菌数N（t）后，水产品剩余货架期也可以计算出来。由Gompertz模型可以推导出下面的货架期预测公式：

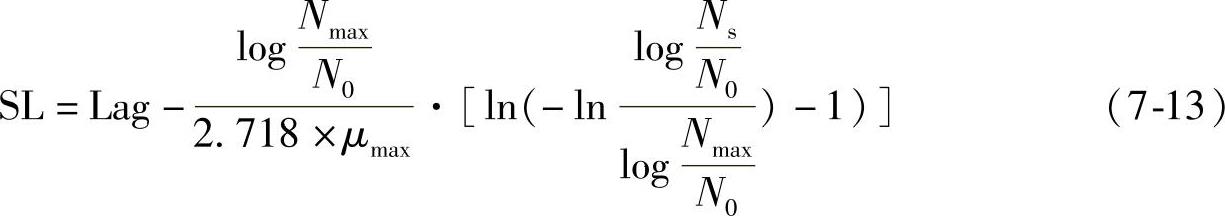
应用SSO的生长模型进行货架期预测时，需要具体分析环境（温度）信息，建立以SSO的生长模型为基础的数据库。其首要条件是开发合适的数据采集装置，记录贮藏中环境的变化，从而依据数据库中贮存的SSO生长动力学数据快速预测货架期。

上述对预测食品货架期的动力学模型进行了详细的阐述，从研究现状看，对同一研究对象可以有几种预测模型进行回归拟合，但还不能找出一个精确的货架期预测模型，因此，需要进行大量的实验进行验证，以确定最佳的预测模型。