传统的由硬件电路构建的模拟锁相环入锁时间较短,可以保证被锁信号和输出信号的稳态相差,但模拟锁相环中心频率点受压控振荡器限制而导致频率范围较窄,环路带宽较宽,当被锁信号瞬间变化时,压控振荡器输出信号发生较大的频率瞬变。随着数字信号处理技术在电力电子领域应用日趋广泛,数字化软件锁相环更适合应用于全数字控制的电力电子变换器中。与传统的硬件电路锁相环相比,软件锁相环环路带宽和中心频率可调,外围电路简单,不受温度漂移、直流偏置和器件饱和等模拟电路固有问题的影响。目前在电力电子电路中,常见的锁相环按照交流信号采样方法不同,一般分为基于过零点检测的锁相环、基于静止坐标系的锁相环和基于同步旋转坐标系(SRF)的锁相环。
5.4.2.1 基于过零点检测的软件锁相环
基于过零点检测的锁相环,通常通过滞环比较器将交流电压信号转换为矩形波,然后对矩形波信号进行锁相。对矩形波信号进行锁相,既可以采用前面介绍的硬件锁相环,也可以采用软件锁相环的方法:由数字信号处理器(DSP)的捕获单元在电网电压同步方波信号的每个上升沿到来时,把定时器的计数值读到存储器中,然后在软件上把计数器的值重新归零,为下一周期计数做准备,这时捕获到的计数器的值,就是电网电压的周期值。比较电网电压的周期值和DSP内部锁相值过零点,可以得到DSP锁相角与电网之间的电压相位差关系,如图5-69所示。
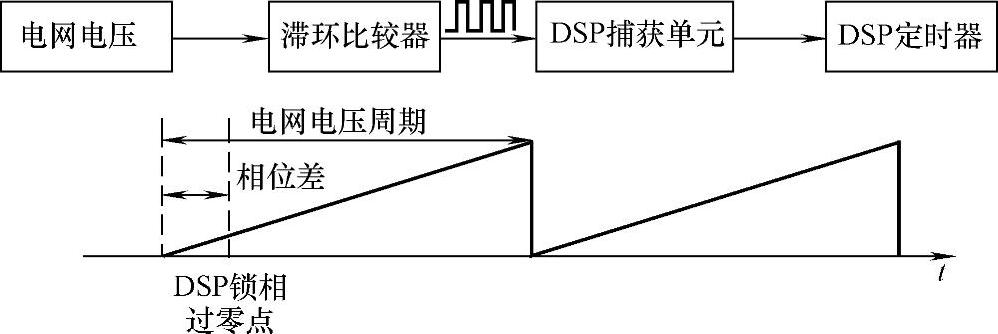
图5-69 DSP锁相角与电网之间的电压相位差关系
图5-69所示的软件锁相环框图中,为了得到电网电压周期和相位信号,首先需要图5-70所示的滞环比较器把调理后的交流电网电压信号v1整形为矩形波信号v2。由于DSP只需要捕获电网电压信号v1的上升沿即可获得交流信号周期和相位信息,因此迟滞比较器的上限触发电平V+为0V,下限触发电平为V-。
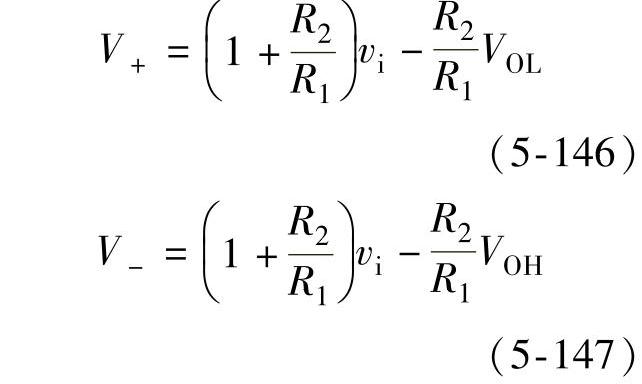
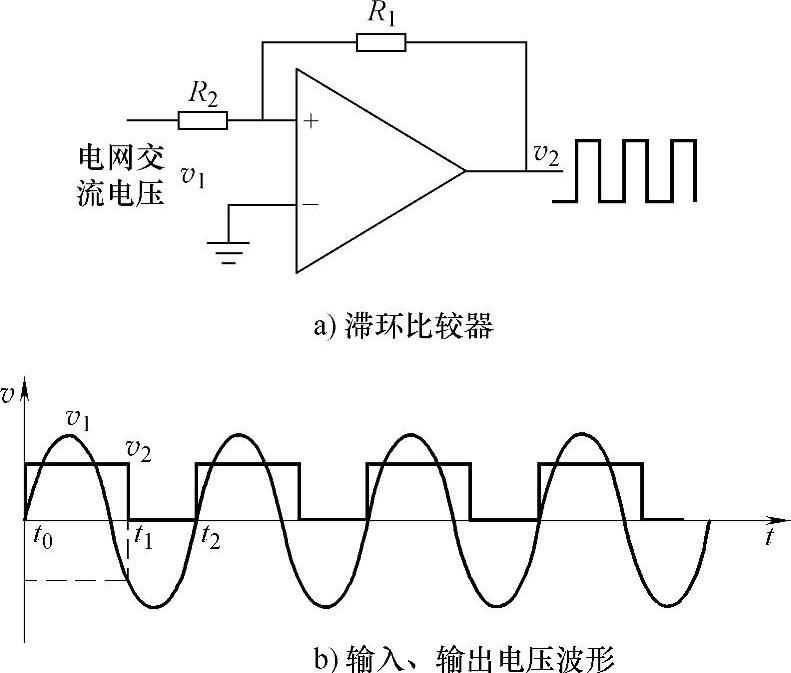
图5-70 滞环比较器及输入、输出电压波形
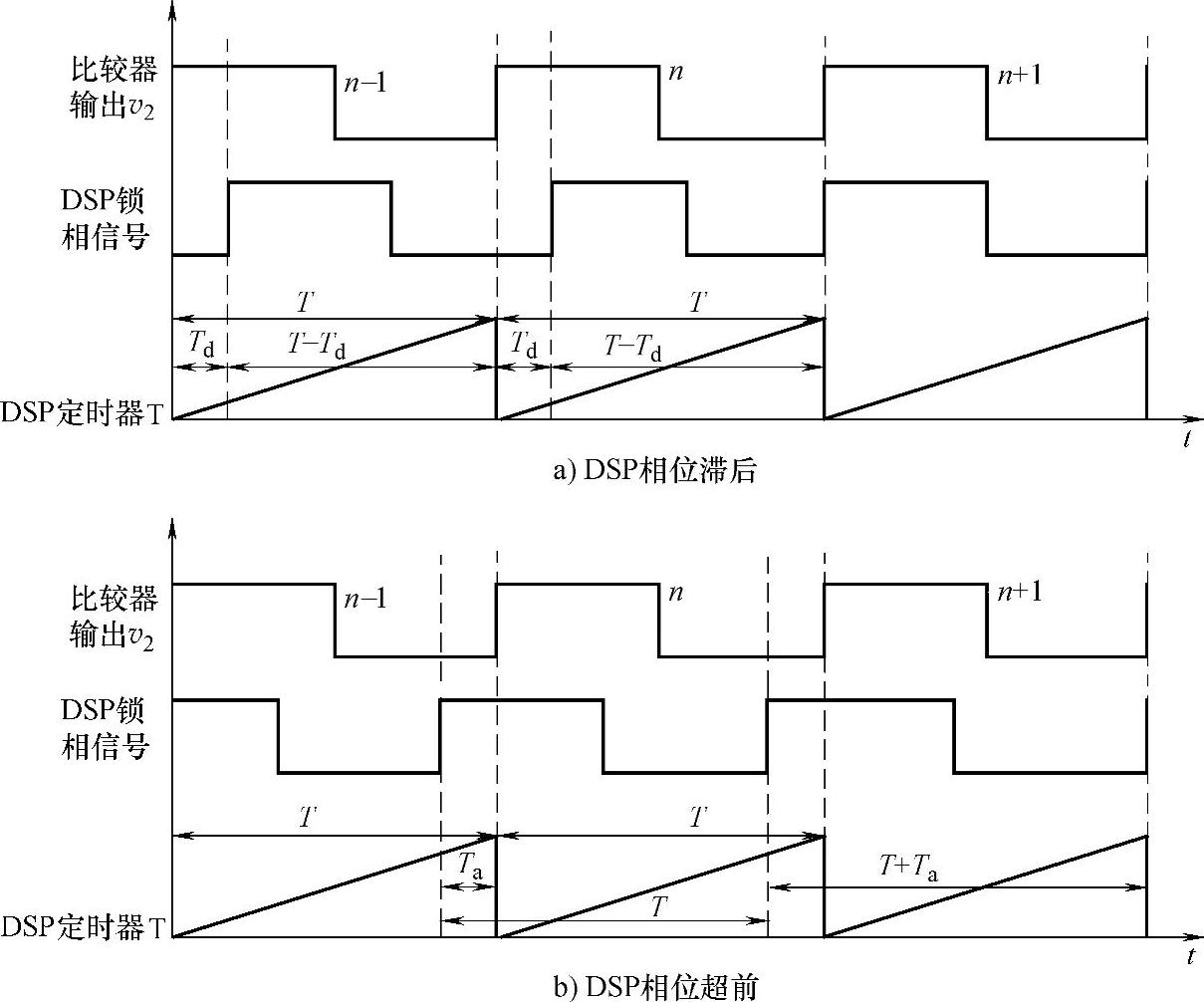
图5-71 数字锁相实现示意图
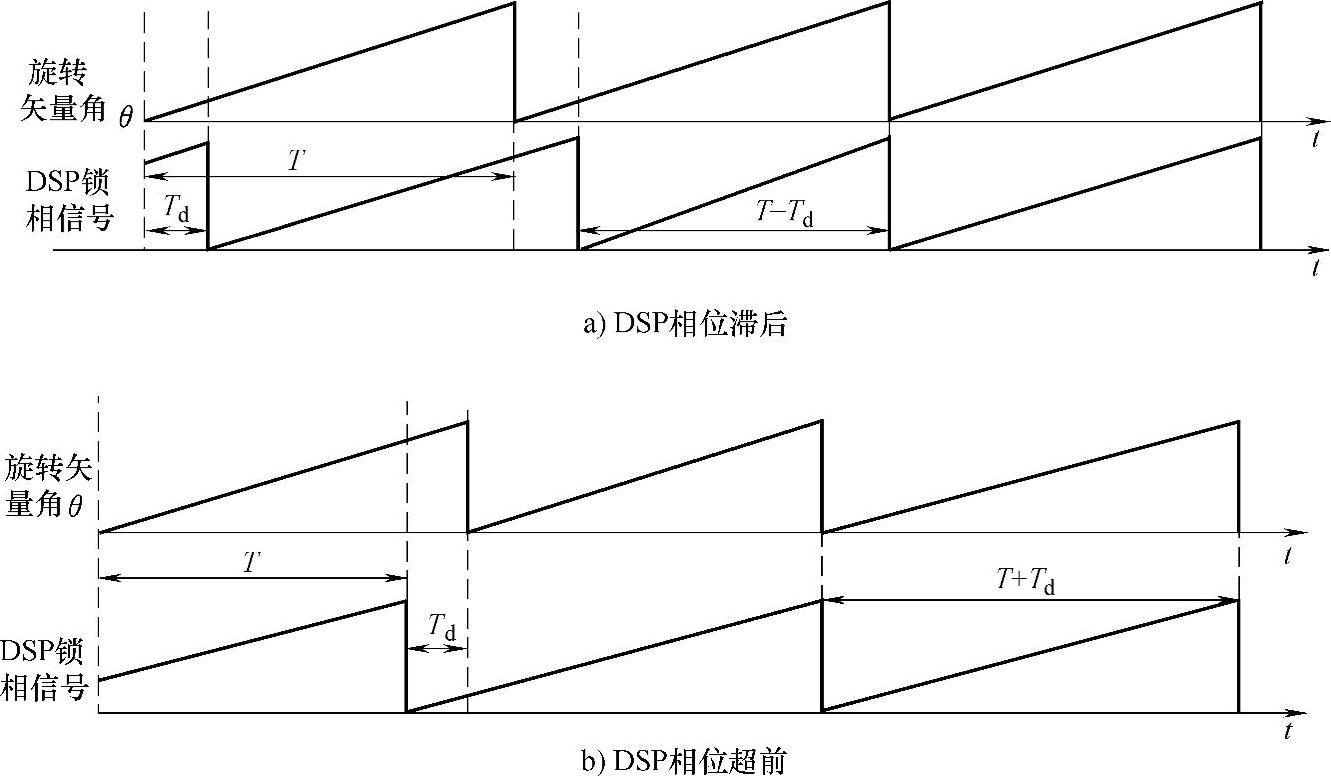
式中,VOH、VOL为滞环比较器输出高、低电平的电压值。图5-71表示了当DSP基准信号滞后和超前于电网电压信号时,数字锁相环的实现过程。在DSP基准信号相位滞后时,在第n-1个周期检测到DSP基准信号滞后电网电压相位为Td(时间)时,则改变第n个周期DSP输出的周期,使其由原来的T变为T-Td,这样在第n+1个周期时,DSP基准信号相位便赶上了电网的相位,DSP输出周期跟踪电网频率,实现同步。在DSP基准信号相位超前时,检测到相位超前量Ta后,在下个周期改变逆变输出频率,使其由原来的T变为T+Ta,以实现同步。为避免因相位差较大而引起DSP输出信号频率剧烈变化,一般需要限制每个周期相位调节的幅度。
在硬件锁相环中,鉴相器的输出代表了相位与频率两种误差,只有在给定输入与反馈输入信号频率相等时,鉴相器输出的才仅仅是相位误差。鉴相器的输出量经滤波后对压控振荡器的控制是将频率与相位一起进行调整的。与硬件锁相环相似,软件数字锁相环也必须对频率和相位分别加以修正,才能达到锁相的目的。在不考虑滤波作用时,对频率的一步修正如下式所示。
Tdsp(n)=TGrid(n-1) (5-148)
式中,Tdsp为DSP锁相基准信号周期;TGrid为电网电压的周期。式(5-148)表示用上一周期电网电压的频率(周期)来作该周期DSP锁相基准信号的频率(周期)。考虑图5-72的RC低通滤波器时,对图中的低通滤波器用后向差分法可以写出其离散化的表达式(即数字滤波器表达式):
Y(n)=AY(n-1)+(1-A)X(n) (5-149)
式中,A表示滤波参数,A=τ/(Ts+τ);τ为时间常数,τ=RC;Ts为采样周期;Y(n)、Y(n-1)为本次和前次滤波值;X(n)为本次采样输入值。在数字锁相环中,将T0(n)作为滤波器的输入,T′(n)作为滤波器的输出,按式(5-149)可得
T′(n)=AT′(n-1)+(1-A)T0(n) (5-150)
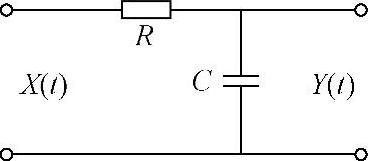
图5-72 RC低通滤波器
在数字锁相环的算式中,仅考虑对频率修正是不够的,因为一旦同步信号的频率发生变化,必然会产生相位误差。数字锁相环中,在调整频率时,也必须调整相位。如果一开始就不修正相位,而仅仅按式(5-150)修正频率,将T′(n)作为DSP锁相基准信号的周期,则无法调整相位差,即相位没有锁定。考虑频率和相位同时修正时,数字锁相环的计算公式为
T(n)=T′(n)+Bθ(n) (5-151)
式中,B为相位修正系数,0<B<1。
根据式(5-150)和式(5-151)即可得数字锁相环的计算公式为
T(n)=AT′(n-1)+(1-A)T0(n)+Bθ(n) (5-152)
式中,T0为捕获单元捕获到的电网电压周期;T′为频率修正后的周期;T为频率修正、相位修正后的周期(数字锁相环的输出频率,也就是DSP锁相基准信号的周期);θ为DSP与电网电压之间的相位差;A为低通滤波器的滤波参数;B为相位修正系数。
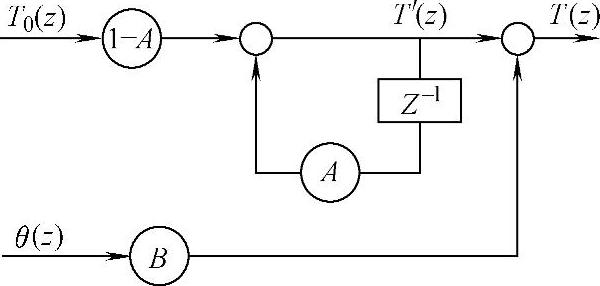
图5-73 数字锁相环的状态变量图
根据式(5-152)可以作出数字锁相环的状态变量图,如图5-73所示。
由此画出数字同步锁相环控制框图,如图5-74所示。电网电压同步信号与DSP锁相基准信号,一方面进行频率修正,另一方面检测出两个信号的相位差。修正后的频率再与检测出来的相位差进行相位修正,相位修正后的频率作为DSP参考正弦波的发生频率。
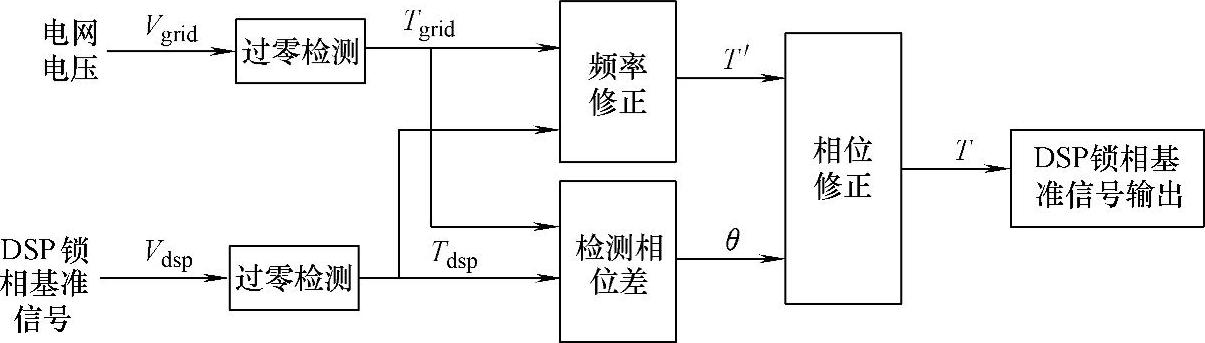
图5-74 数字同步锁相环控制框图
5.4.2.2 基于三相静止坐标系的锁相环
基于交流电压过零点检测的锁相环技术广泛应用于不间断电源等电力电子变换器控制中,该方法优点是操作简单,缺点在于当电网电压畸变严重时,滞环比较器容易发生误动作,并且滞环比较器固定的滞环宽度在电网电压有效值最低和最高时延迟时间有差异。另外对于三相系统,采用基于交流电压过零点检测的锁相环技术需要对各相分别锁相。若能将三相电压用一个合成量表示,而保持电压信息的完整,则三相的问题可以简化为单相的问题,由一个锁相环对三相电压进行锁相。由前面分析可得,采用电压矢量变换,abc坐标系下的三相系统可以变换到αβ静止坐标系下。对应三相正弦电网电压的空间电压矢量的顶点运动轨迹是一个圆,圆的半径为相电压的幅值,空间矢量以工频角速度ω按逆时针方向匀速旋转。对旋转矢量在α轴和β轴投影进行反正切变换,可以得到旋转矢量角θ,如图5-75所示。
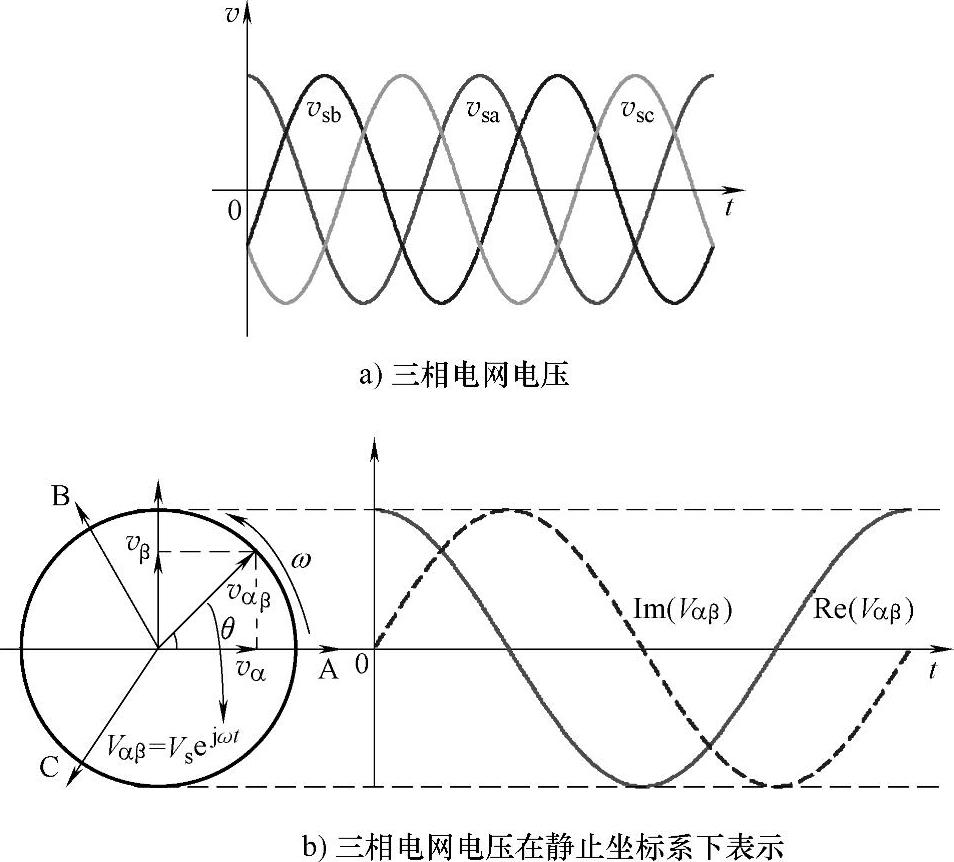
图5-75 三相电网电压及其在静止坐标系下表示
图5-75中,三相电压表示为
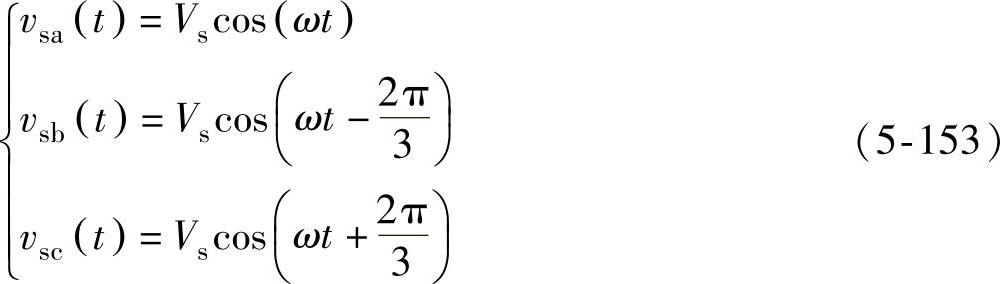
式中,Vs为相电压峰值。αβ静止坐标系下电压空间矢量Vαβ表示为
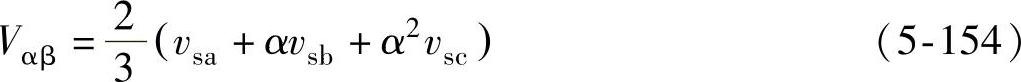
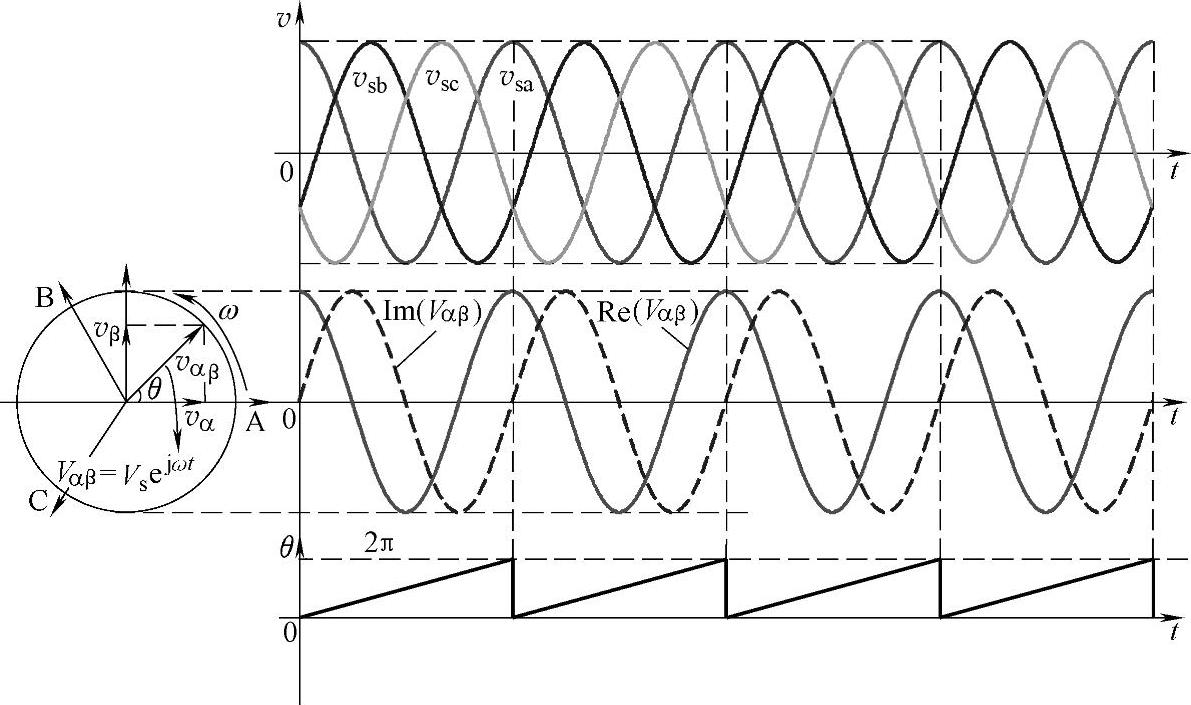
图5-76 三相电网电压对应的旋转矢量角
在图5-75中,电压空间矢量Vαβ、旋转矢量角θ如图5-76所示。θ表示为
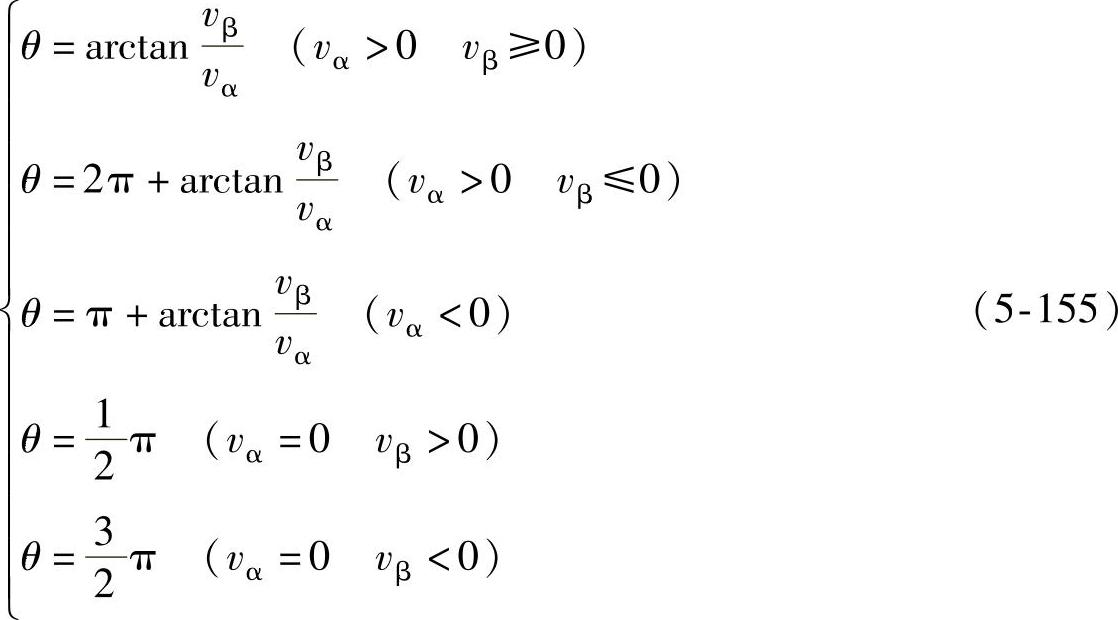
由图5-76可知,三相正弦电压旋转矢量角θ在一个工频周期内角度随时间从0到2π线性变化,因此可以对三相正弦电压旋转矢量角θ进行锁相。
图5-77表示了当DSP基准信号滞后和超前于电网电压信号时,数字锁相环的实现过程。在DSP基准信号相位滞后时,在第n-1个周期检测到DSP基准信号滞后电网电压相位为Td(时间)时,则改变第n个周期DSP输出的周期,使其由原来的T变为T-Td,这样在第n+1个周期时,DSP基准信号相位便赶上了电网的相位,DSP输出周期跟踪电网频率,实现同步。在DSP基准信号相位超前时,检测到相位超前量Ta后,在下个周期改变逆变输出频率,使其由原来的T变为T+Ta,以实现同步。为避免因相位差较大而引起DSP输出信号频率剧烈变化,一般需要限制每个周期相位调节的幅度。
 (https://www.xing528.com)
(https://www.xing528.com)
图5-77 数字锁相环实现示意图
与基于过零信号的锁相环方法相同,数字锁相环公式为
T(n)=AT′(n-1)+(1-A)T0(n)+Bθ(n) (5-156)
式中,T0为按照电网电压旋转矢量计算得到的电网电压周期;T′为DSP锁相信号的周期;T为DSP锁相信号频率修正、相位修正后的周期(数字锁相环的输出频率,也就是DSP锁相基准信号的周期);θ为DSP基准信号与电网电压之间的相位差,A为低通滤波器的滤波参数;B为相位修正系数。
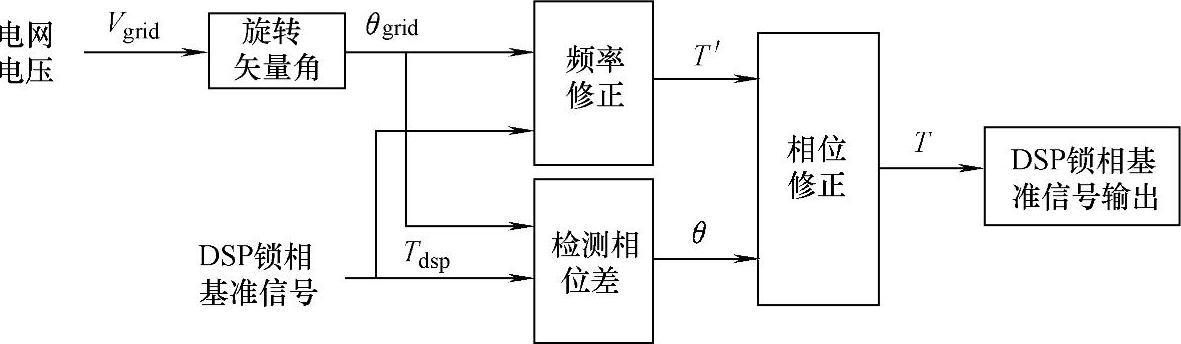
图5-78 数字同步锁相环控制框图
由此画出数字同步锁相环控制框图,如图5-78所示。电网电压同步信号与DSP锁相基准信号,一方面进行频率修正,另一方面检测出两个信号的相位差。修正后的频率再与检测出来的相位差进行相位修正,相位修正后的频率作为DSP参考正弦波的发生频率。
上述基于三相静止坐标系的锁相环,每个电网电压工频周期进行一次锁相环计算,电网电压频率突变时锁相环难以快速捕获,动态特性不佳。为了提高锁相环动态特性,可以提高锁相环计算频率。设三相电网电压表示为
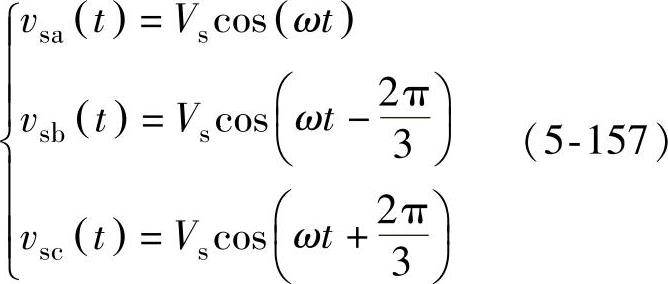
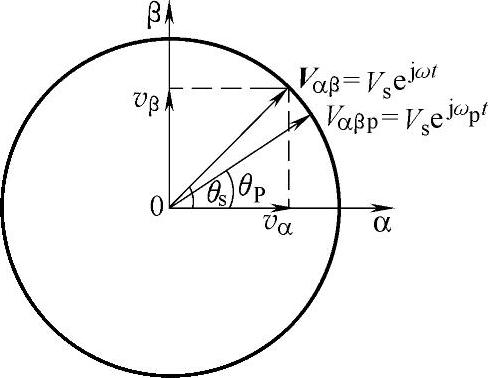
图5-79 实际电网电压旋转矢量Vαβ和虚拟旋转矢量Vαβp
式中,Vs为电网电压基波幅值;ω=2πf,f为电网电压基波频率。经过Clark坐标变换得到αβ静止坐标系下的电网电压为

由式(5-158)得到电网电压在αβ静止坐标系下的表示形式,设电网电压在αβ静止坐标系下的旋转矢量角为θs,DSP软件锁相环锁相角为θp,如图5-79所示,则有

因此,可以得到电网电压旋转矢量角和DSP锁相角之间的相位误差信号δ(t)为
δ(t)=ωt-ωpt (5-160)
由此,可画出基于αβ静止坐标系下的锁相环线性化模型,如图5-80所示。图5-80中,PLL角频率为
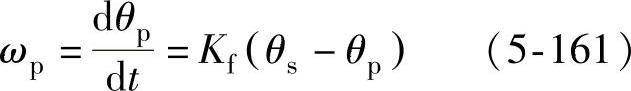
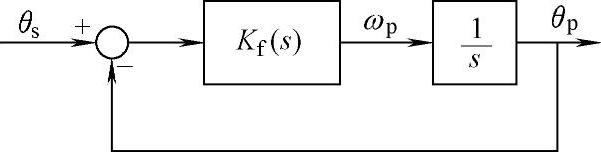
图5-80 基于αβ静止坐标系下的PLL线性化模型1
式中,Kf为PLL环路滤波器增益。图5-80所示的线性化模型的闭环传递函数表示为
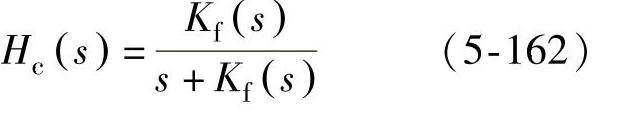
式(5-162)中,环路滤波器Kf(s)的设计决定了锁相环的跟踪性能。通常比例积分(PI)调节器可以较好地满足滤波器性能和系统稳定性。

结合式(5-162)和式(5-163),闭环传递函数可以表示为

式中

在实际的基于αβ静止坐标系下的锁相环系统中,为了提高系统跟踪性能,一般把电网电压额定角速度以前馈方式加入到锁相环模型中,如图5-81所示。
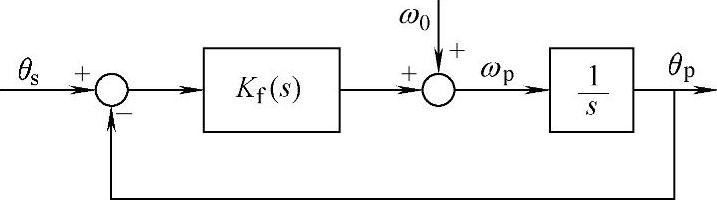
图5-81 基于αβ静止坐标系下的PLL线性化模型2
5.4.2.3 基于同步旋转坐标系的锁相环
按照基于αβ静止坐标系下的锁相环思路,也可以构建基于同步旋转坐标系的锁相环。由式(5-158)得到电网电压在αβ静止坐标系下的表示形式,经过Park坐标变换可得到dq坐标系的电网电压为
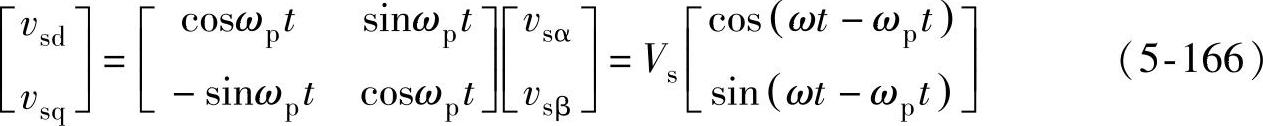
式中,ωp为锁相环的输出。当电网电压相位角与锁相环输出的相位角之间的差值较小时,式(5-166)可近似为
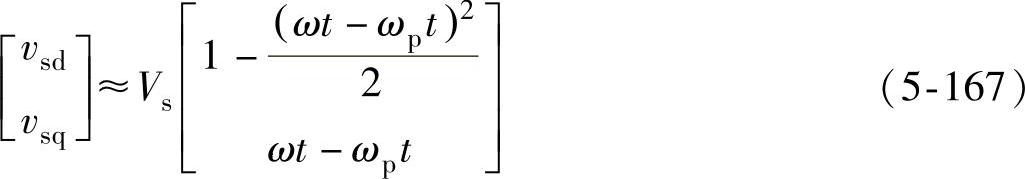
因此,可用vsq来表达相位的误差信息e(t),即有
vsq≈Kd(ωt-ωpt)=Kde(t) (5-168)
式中,Kd为鉴相器的增益,Kd=Vs。
由此,可画出基于dq坐标系的线性化锁相环模型,如图5-82所示。
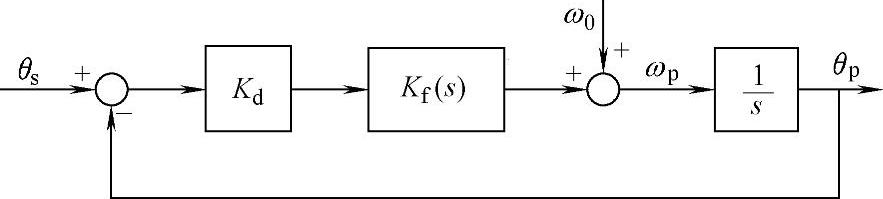
图5-82 线性化PLL模型
根据图5-82,锁相环最终达到的效果是DSP锁相角θp无限接近电网电压旋转矢量角θs,即根据锁相角θp计算得到的电网电压q轴分量逼近零,因此可以得到基于dq坐标系的锁相环路模型如图5-83所示。
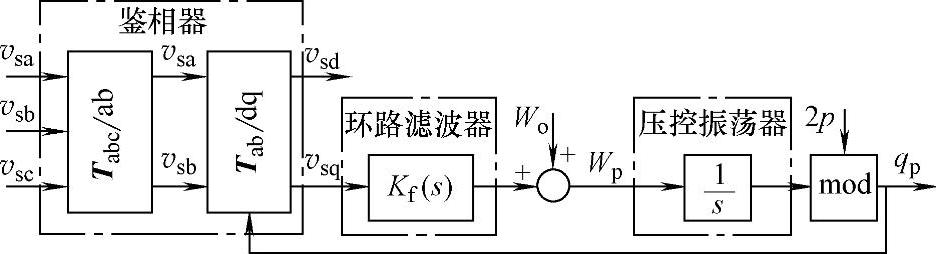
图5-83 基于dq坐标系的锁相环路模型
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




