在三相电网中,如果电压和电流具有相同的幅值、并且相位互相差120°,则被称为平衡或对称的系统。如果其中的一个或两个条件不满足,则称为不对称或不平衡的系统。在非理想电网条件下,根据电路基本理论,三相不对称电网电压如下式所示:
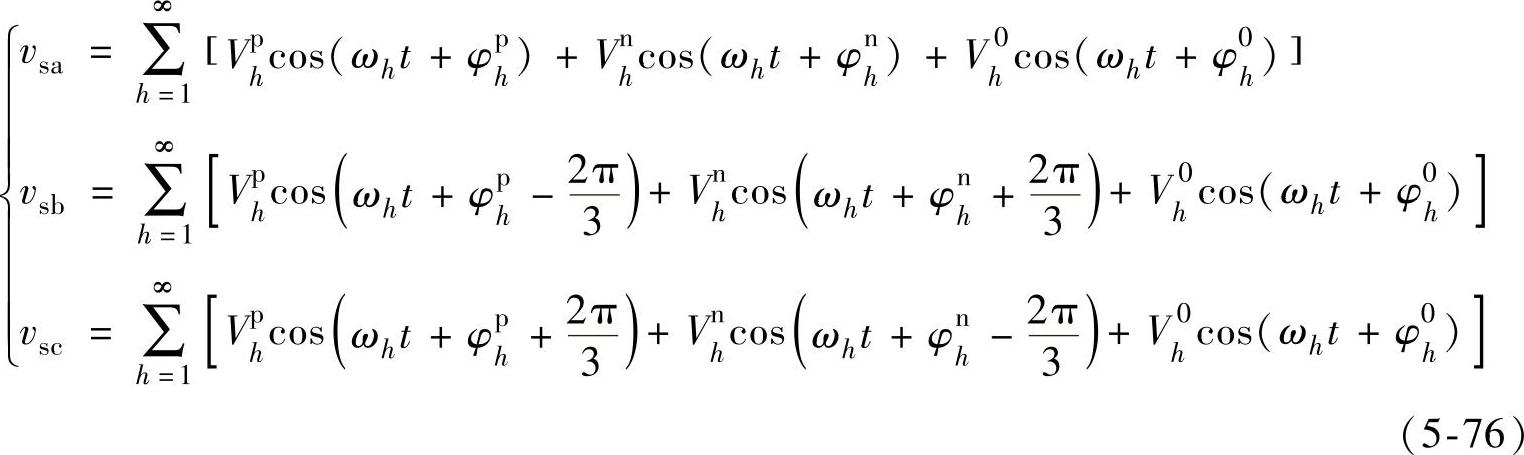
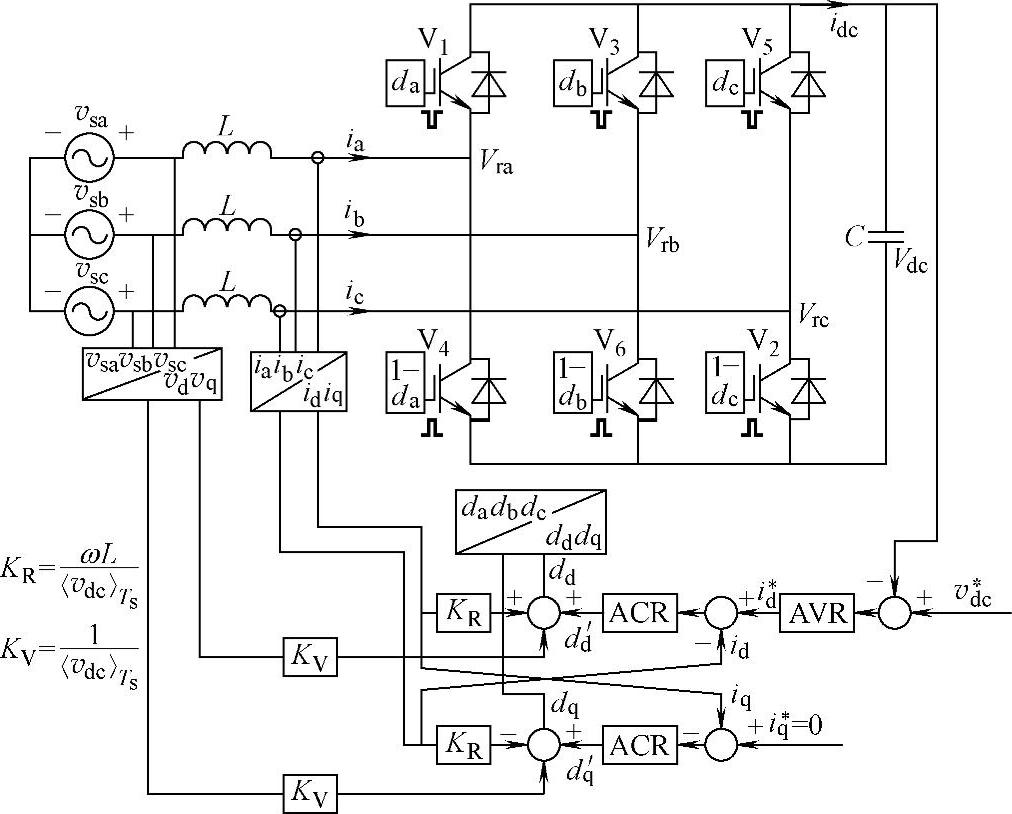
图5-33 解耦后三相三线PWM整流器整体控制框图
式中,Vph、Vhn、V0h分别为电网电压h次分量的正序、负序、零序幅值;φhp、φnh、φ0h分别为电网电压h次分量的正序、负序、零序初始相位;ω为电网电压h次分量的角频率。如果只考虑电网电压基波分量,则三相不对称电网电压不平衡度εV定义为电压基波负序分量有效值与正序分量有效值之比:

按照Park变换定义,引入电压空间矢量V

把电压空间矢量V相应地分解为正序分量和负序分量如下式所示:
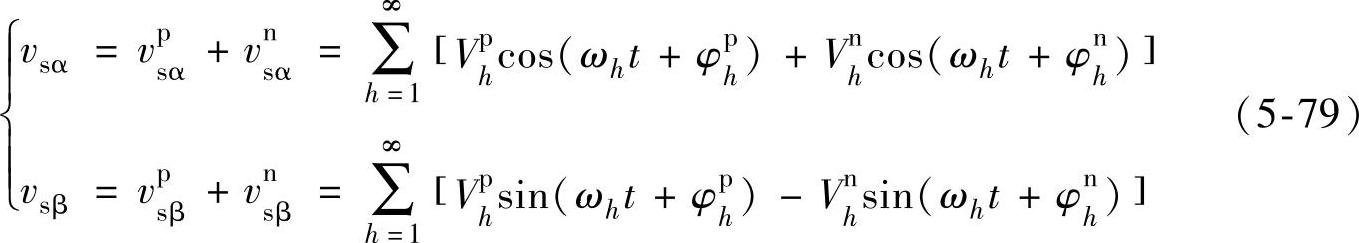
对式(5-79)进行正序和负序旋转的Clark变换,变换式如下:
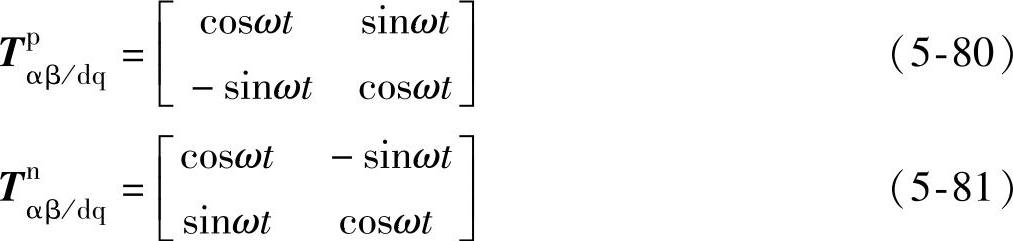
采用式(5-80)把αβ坐标系下电网电压旋转矢量变换到正序同步旋转坐标系下,结果如下式所示:
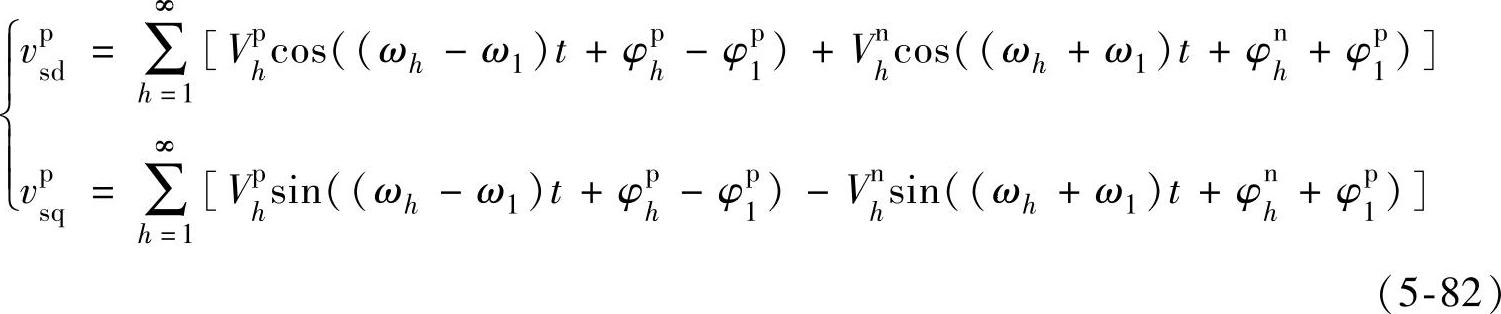
由式(5-82)可以得到式(5-76)所示的不平衡电网电压中的基波正序分量将转换成直流量,基波负序分量转换成频率为2f1的交流量,低次谐波中5次正序和7次负序分别转换成频率为4f1、8f1的交流量,5次负序、7次正序分量转换成频率为6f1的交流量。如果只考虑电网电压基波分量,则有
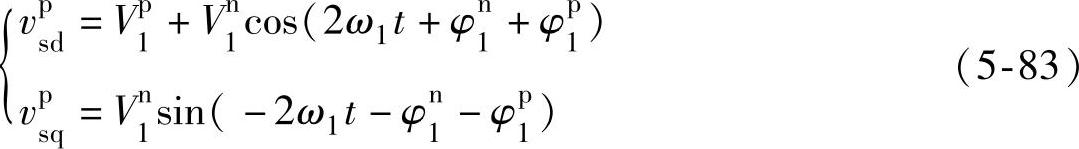
根据式(5-83)可以得到,当三相电网电压存在负序分量时,同步旋转坐标系下旋转电压d轴分量vsd和q轴分量vsq均存在两倍频脉动量,vsd的直流分量等于正序电网相电压峰值,vsq的有效值等于负序电网相电压有效值。
采用式(5-81),把αβ坐标系下电网电压旋转矢量变换到负序同步旋转坐标系下,结果如下式所示:
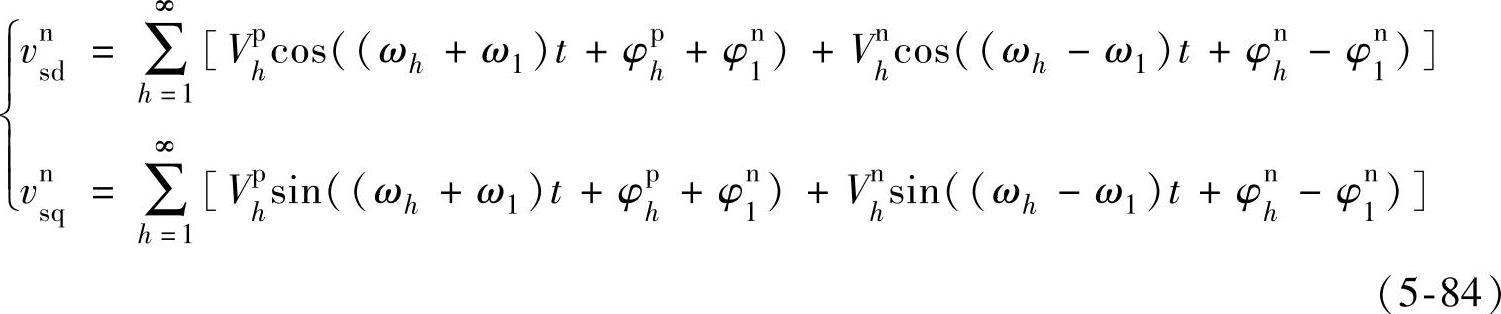
由式(5-84)可以得到式(5-76)所示的不平衡电网电压中的基波负序分量将转换成直流量,基波正序分量转换成频率为2f1的交流量,低次谐波中7次正序和5次负序分别转换成频率为8f1、4f1的交流量,低次谐波中7次负序、5次正序分量转换成频率为6f1的交流量。如果只考虑电网电压基波分量,则下式成立:
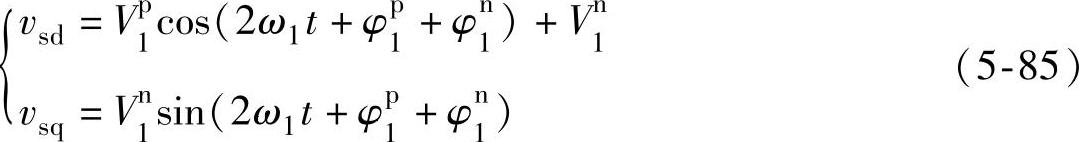
根据式(5-85)可以得到,当三相电网电压存在负序分量时,同步旋转坐标系下旋转电压d轴分量vsd和q轴分量vsq均存在两倍频脉动量,vsd的直流分量等于负序电网相电压峰值,vsq的有效值等于正序电网相电压有效值。
根据式(5-83)和式(5-85)可以得到,当三相电网电压基波不平衡时,无论采用正序同步坐标系旋转变换还是负序同步坐标系旋转变换,最终在同步坐标系下的d轴和q轴分量均存在两倍频脉动量。根据前面分析,之所以把同步旋转坐标变换引入三相整流器控制中,是由于整流器三相电压、电流量在同步坐标系下为直流量,使补偿器设计方便。当电网电压基波不平衡时,仍然希望继续利用同步旋转变换的这一特点。分析式(5-83)和式(5-85)可知,如果只考虑电网电压基波分量,则三相电网电压在正序旋转坐标系下表现为直流分量和两倍基频的负序交流分量的叠加,其中直流分量等于电网正序相电压的峰值;三相电网电压在负序旋转坐标系表现为直流分量和两倍基频的正序交流分量的叠加,其中直流分量等于电网负序相电压的峰值。如果可以对正、负序进行分离,对正序量采用正序同步旋转坐标系、对负序量采用负序同步旋转坐标系,则在正、负序同步旋转坐标系下,三相整流器的正、负序电压、电流分量均表示为直流量,同步旋转控制的优势就可以体现出来。对三相不对称电网电压进行正、负序分离有多种方法。图5-34所示的框图采用低通滤波器进行不对称电网电压的正、负序分离,在正序旋转坐标系下,不对称电网电压的基波负序分量表现为两倍频脉动量,采用低通滤波器对2次及以上的脉动量进行滤波,滤波后进行反Park变换和反Clark变换得到的就是不对称电网电压的正序分量,不对称电网电压减去相应相的正序分量,剩下的就是负序分量,从而实现电网电压正、负序分离。图5-35所示的框图采用100Hz陷波器对电网电压在正序和负序旋转坐标系下的d轴和q轴电压矢量进行滤波,得到的直流分量就可以分别对应三相电网电压的正序和负序分量。该方法的缺点是当电网电压频率变化时,陷波器设计较为困难。
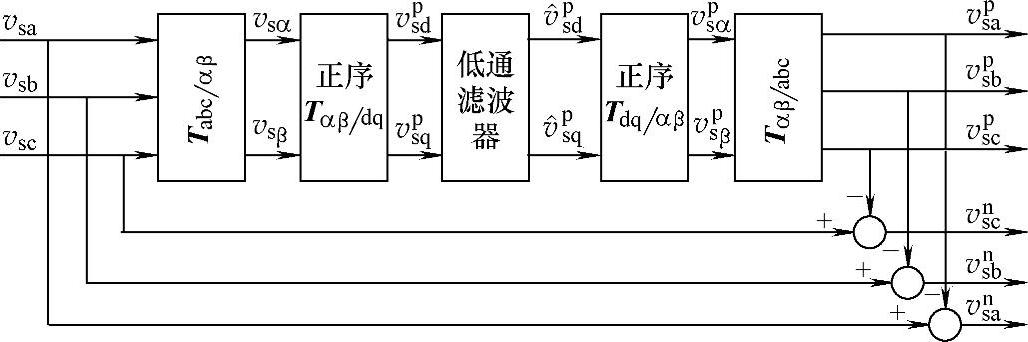
图5-34 低通滤波器正、负序分离
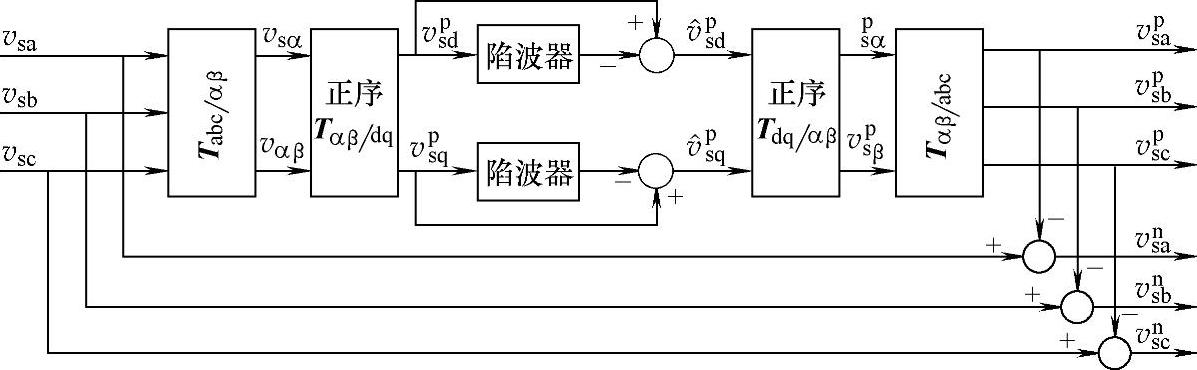
图5-35 陷波器正、负序分离
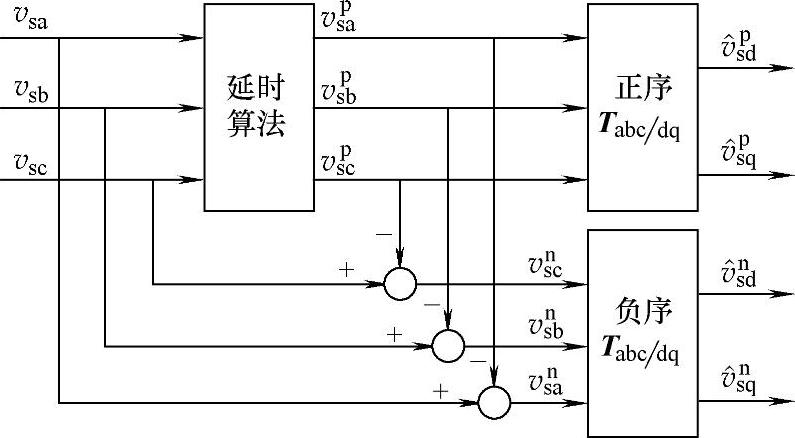
图5-36 延时算法正、负序分离
图5-36所示的框图采用延时算法进行正、负序分离。式(5-86)所示的基于abc坐标系的延时算法,可以有效分离电网电压正序分量,其最大采样延时时间为Ts/3。采用信号延时算法进行正负序分离的优点是不需要滤波器。
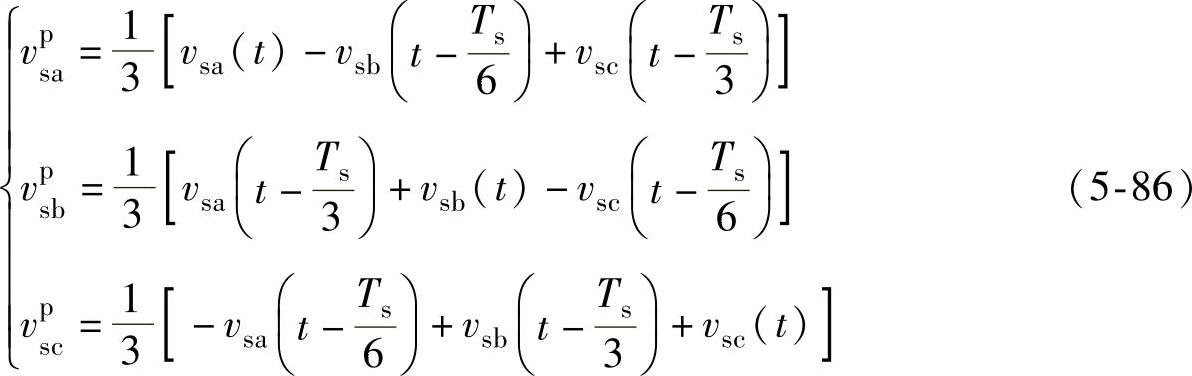
按照式(5-86)所示方法,经过Ts/3就可以提取出正序分量。由式(5-86)所得到的三相正序电压经过Clark和正序Park变换,可写出dq坐标系下的电压表达式为
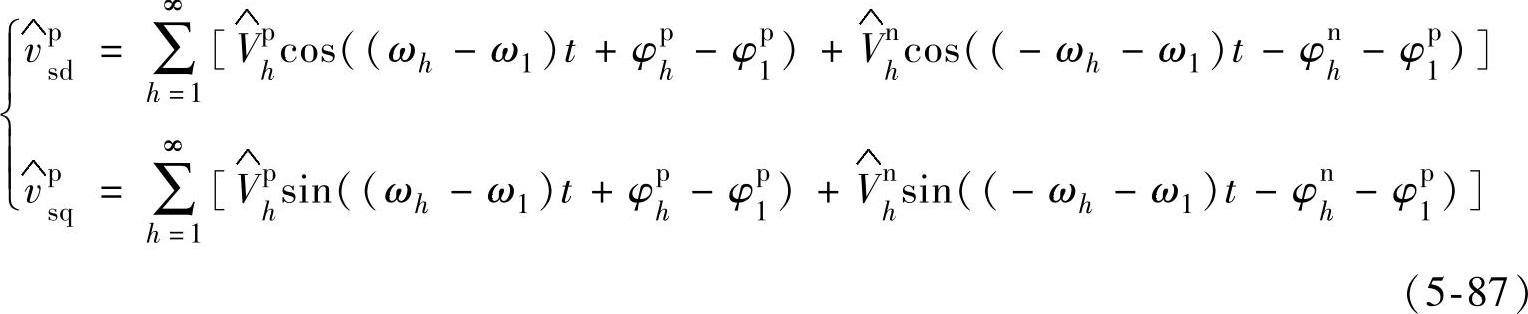
式中
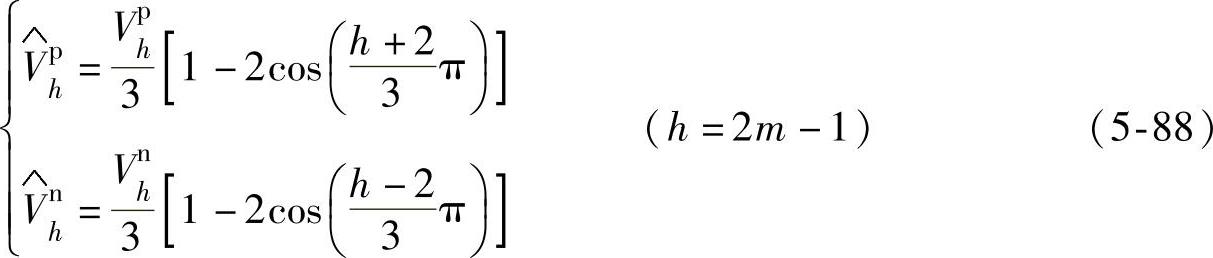
由式(5-88)可知,采用基于abc坐标系的延时算法进行正序分离后,能够消除因基波负序分量而产生的频率为2f1的脉动量,同时也消除了因5次正序、7次负序谐波成分而引入的频率为4f1、8f1的脉动量。
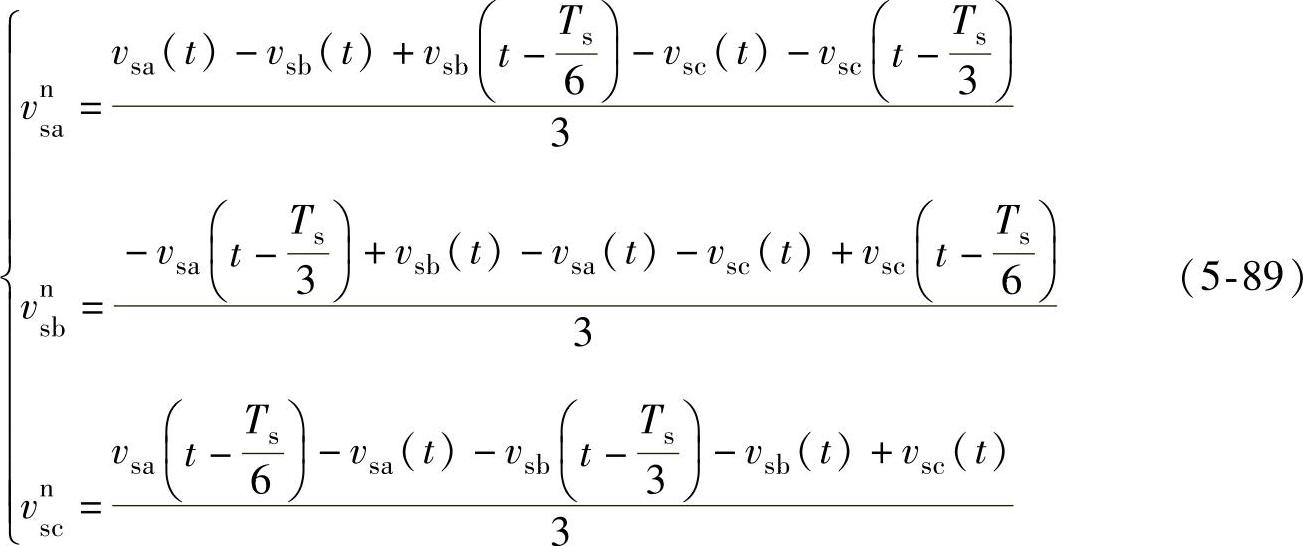
采用式(5-89)所示的基于abc坐标系的延时算法,可以有效地分离电网电压负序分量,其最大采样延时时间为Ts/3。按照式(5-89)所示方法,经过Ts/3就可以提取出负序分量。由式(5-89)所得到的三相正序电压经过Clark和负序Park变换,可写出dq坐标系下的电压表达式为
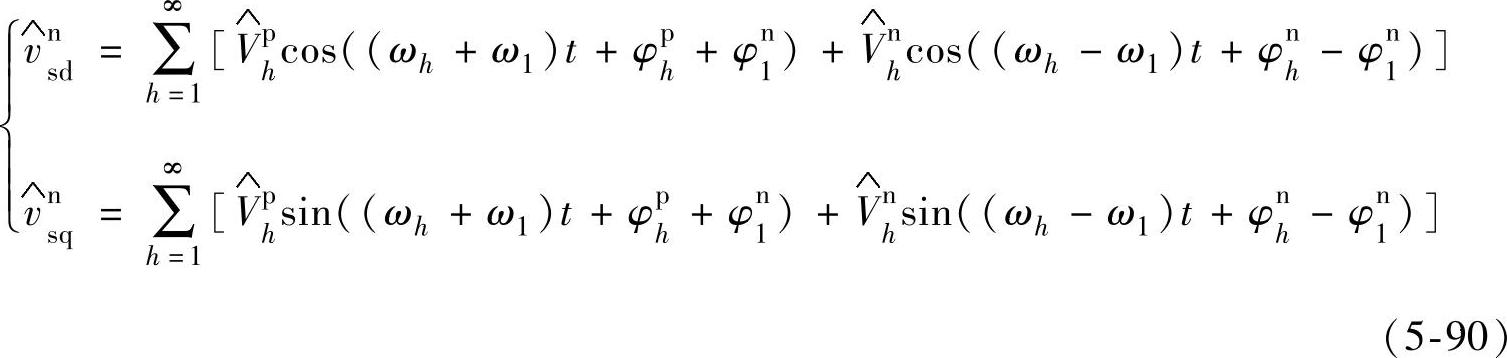 (https://www.xing528.com)
(https://www.xing528.com)
式中
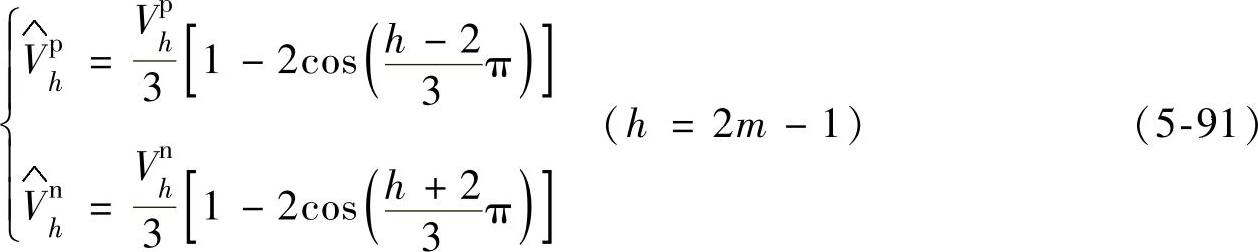
由式(5-91)可知,采用基于abc坐标系的延时算法进行负序分离后,能够消除因基波正序分量而产生的频率为2f1的脉动量,同时也消除了因5次负序、7次正序电压谐波成分而引入的频率为6f1的脉动量。
根据上述分析得到
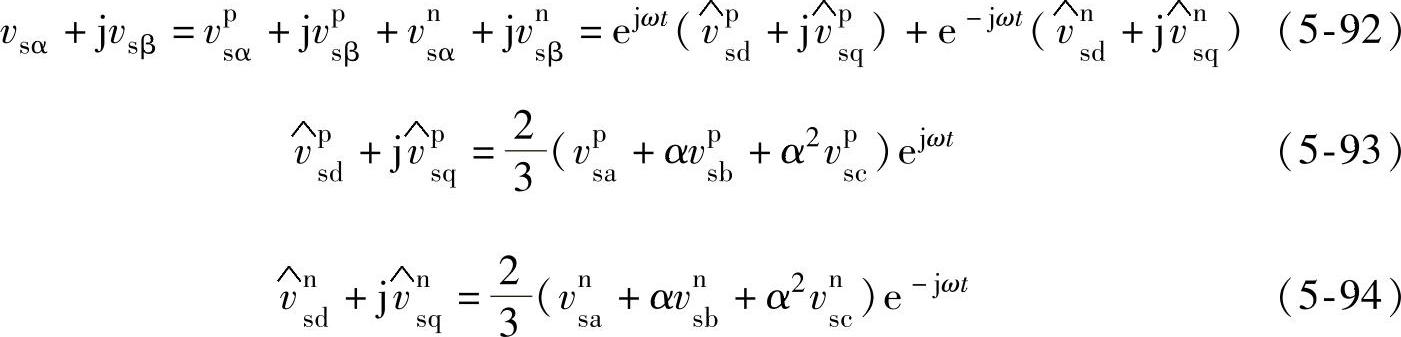
由式(5-93)、(5-94)可得按照正序和负序坐标变换得到的电网电压正序和负序电压矢量,与时间轴上三相电网电压的正序和负序分量存在一一对应关系,据此可以设计三相PWM整流器在电网电压不对称情况下的控制算法如下:
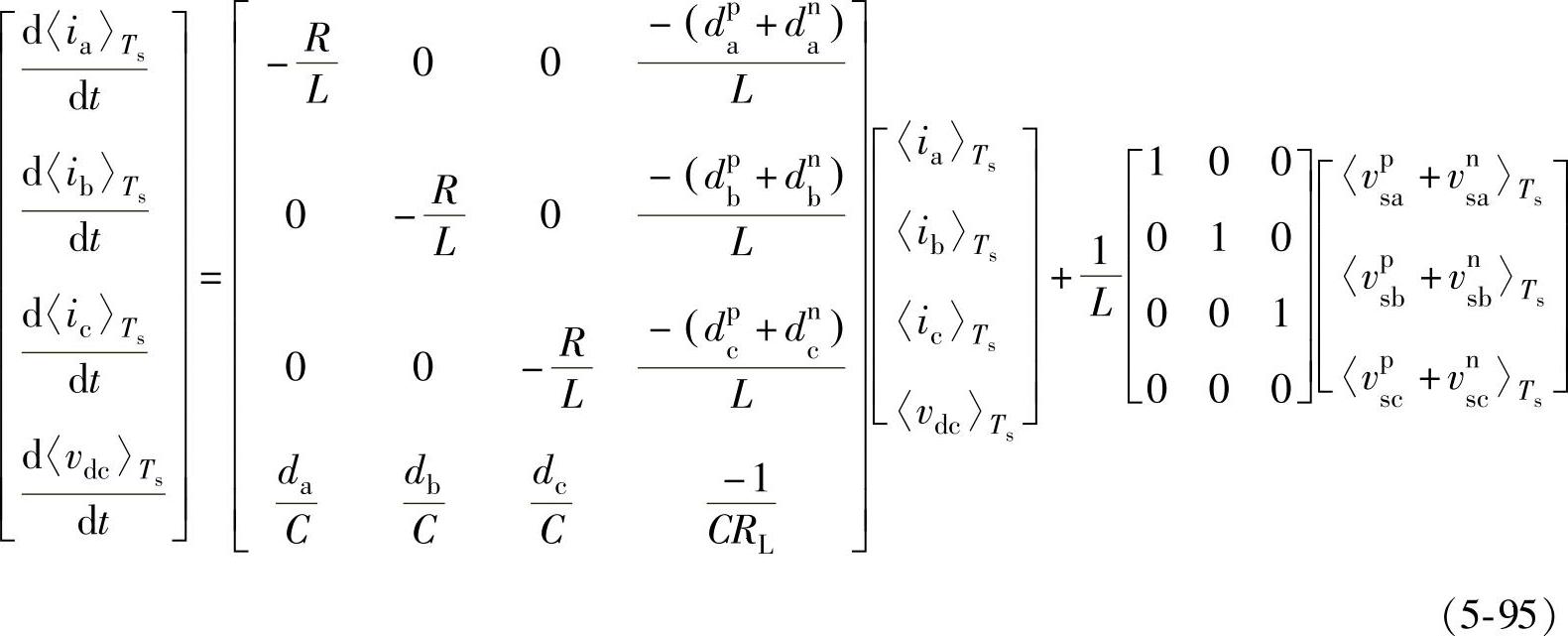
重写式(5-18)和图5-4如式(5-95)和图5-37所示。根据式(5-95)和图5-37可以得到整流器交流侧被分解为三个完全解耦的单相交流电路,电网电压零序分量和整流器调制电压零序分量都不会影响整流器交流电流,只会影响整流器交流侧虚拟参考点和直流电压参考地之间的电位差。
分解式(5-95)可以得到下式:
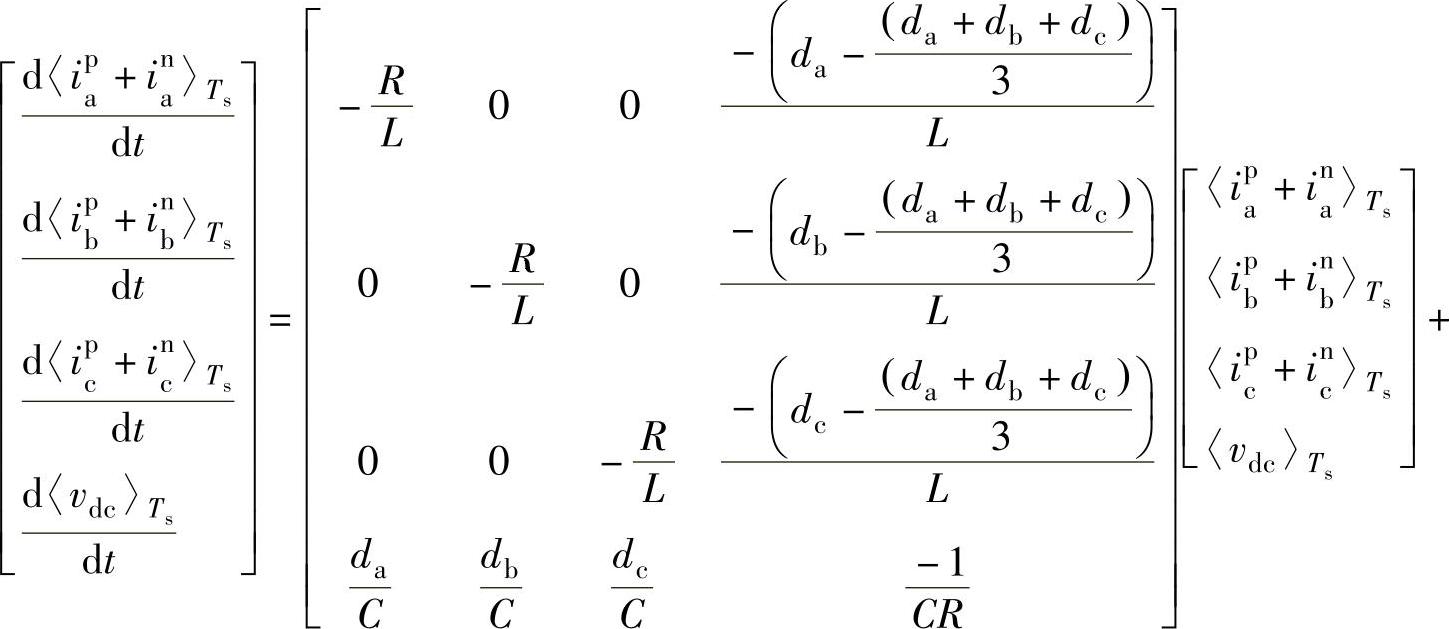
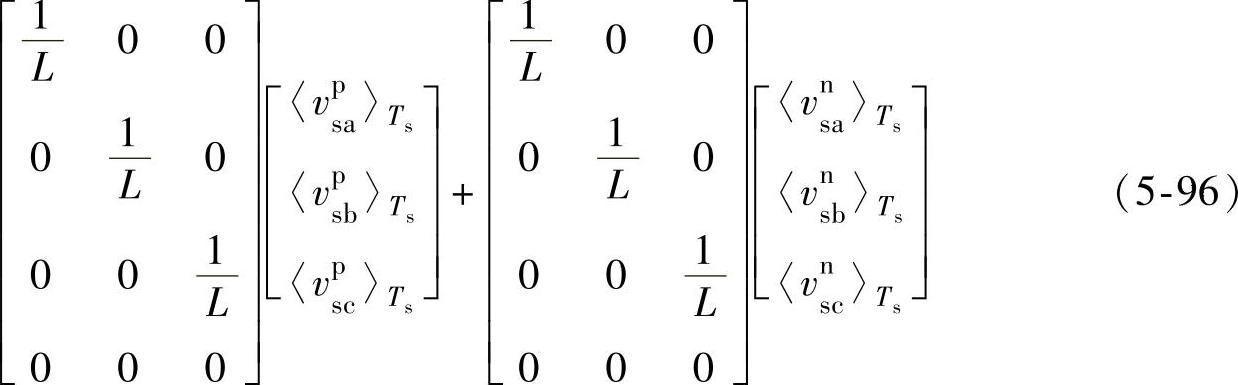
根据电路基本理论,结合式(5-96),图5-37所示的开关周期平均模型,可以分解为两个独立的正序和负序模型,如图5-38所示。
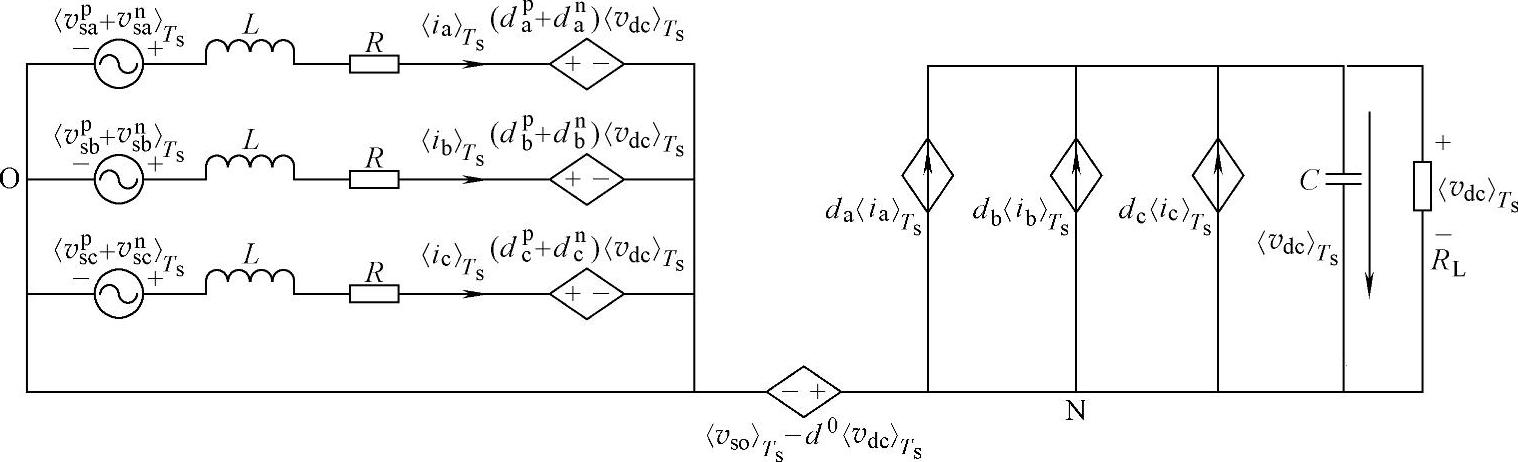
图5-37 三相三线PWM整流器的开关周期平均模型1
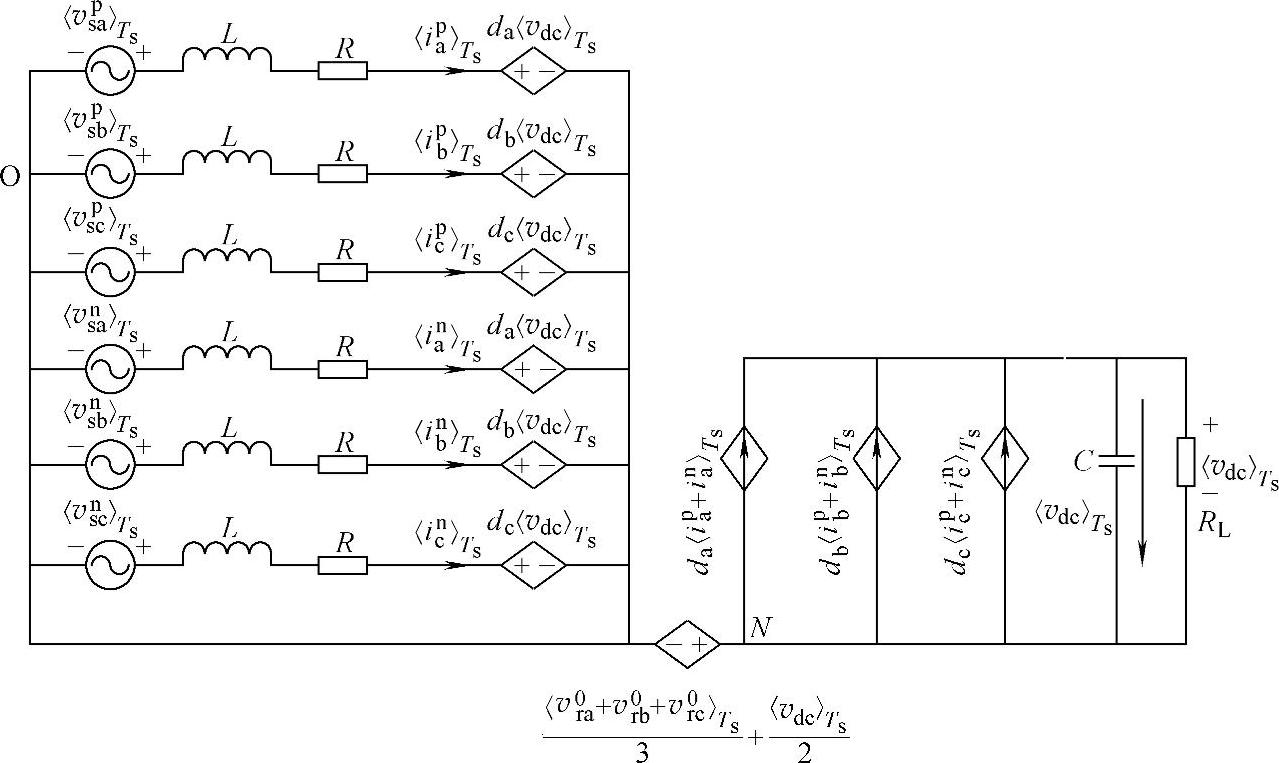
图5-38 三相三线PWM整流器的开关周期平均模型2
由式(5-93)、式(5-94)对式(5-96)的正序和负序分量分别进行正序和负序同步坐标变换,得到

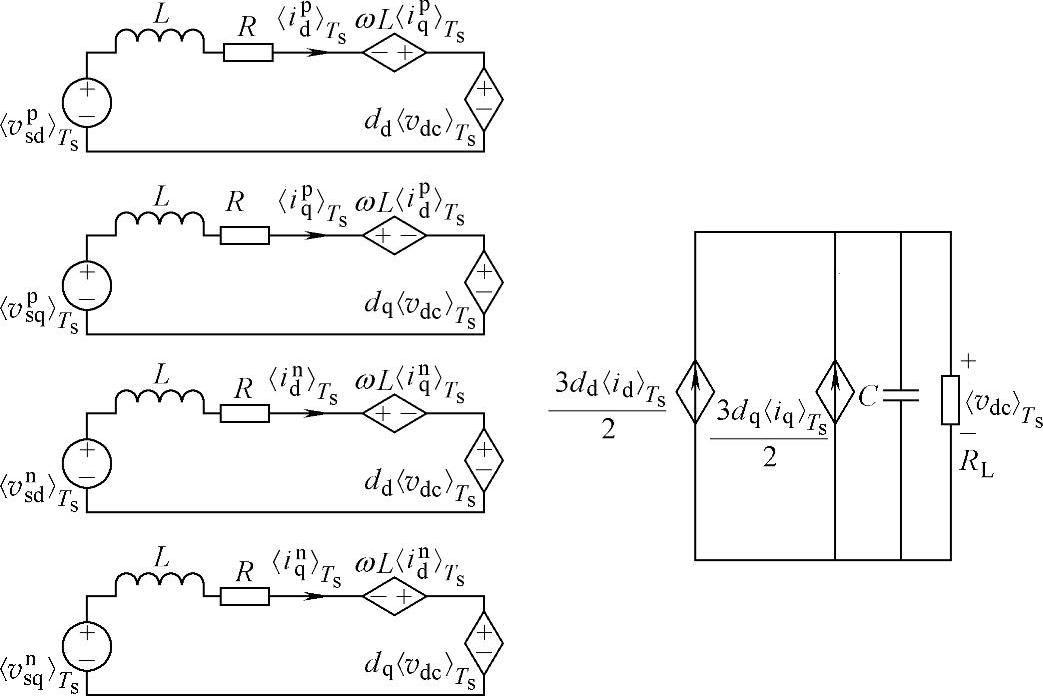
图5-39 三相三线PWM整流器在同步旋转坐标系下开关周期平均模型等效电路
根据式(5-97)可以得到在正序和负序同步旋转坐标系下,PWM整流器分离出的正序电压、电流分量和负序电压、电流分量在交流侧相互解耦,如图5-39所示。因此,可以在正序和负序旋转坐标系下,对整流器正序和负序分量分别进行控制。
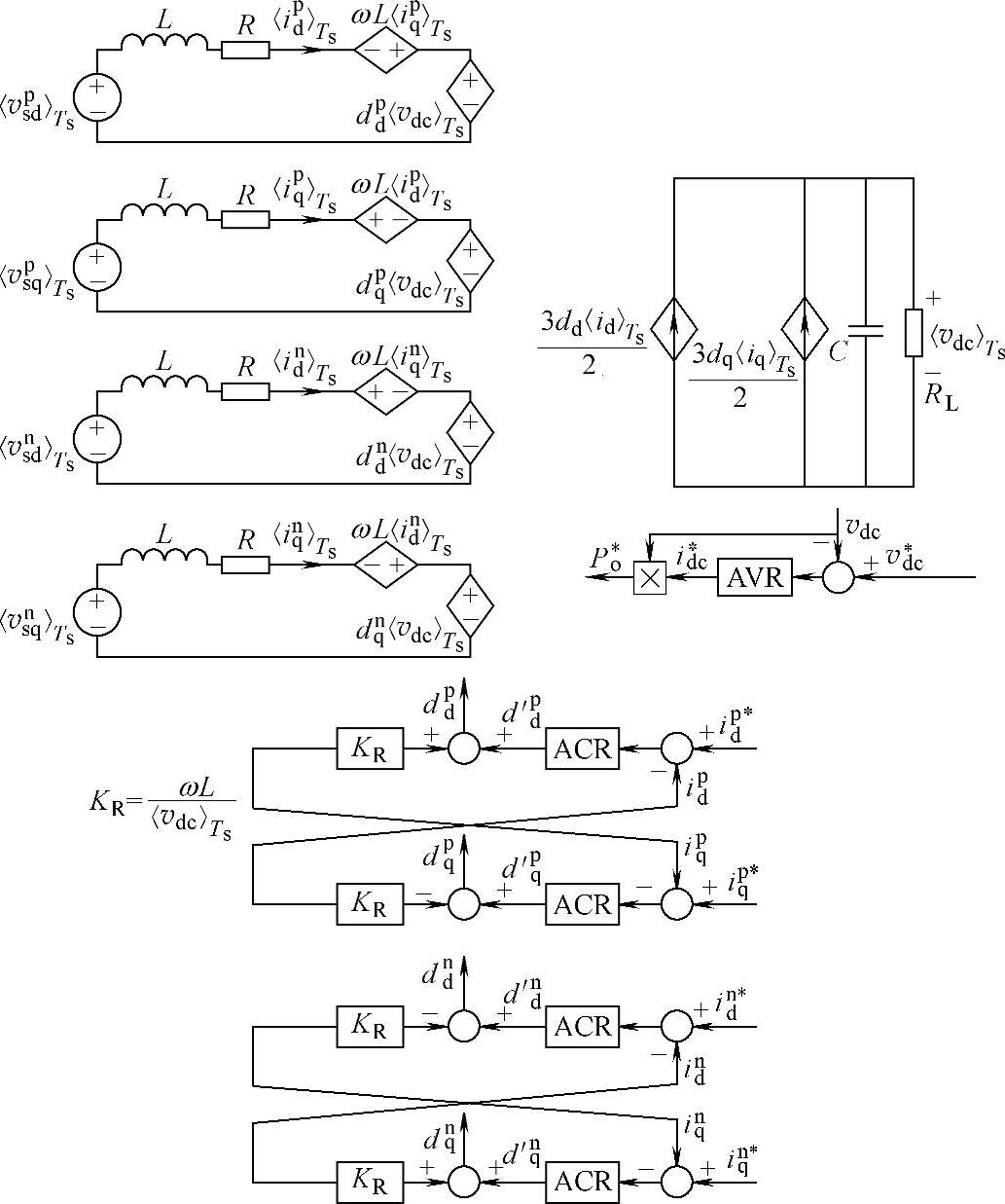
图5-40 PWM整流器在正、负序同步旋转坐标系下开关周期平均模型控制框图
PWM整流器在正、负序同步旋转坐标系下开关周期平均模型控制框图如图5-40所示。根据式(5-97),在正序和负序同步旋转坐标系下,PWM整流器的正序电压、电流分量和负序电压、电流分量在交流侧相互解耦,因此只要给定整流器正序和负序电流基准,就可以对整流器网侧电流进行控制。如何给定整流器正序和负序电流基准,主要取决于不同的功率控制策略。在静止坐标系下,PWM整流器网侧输入功率表示为
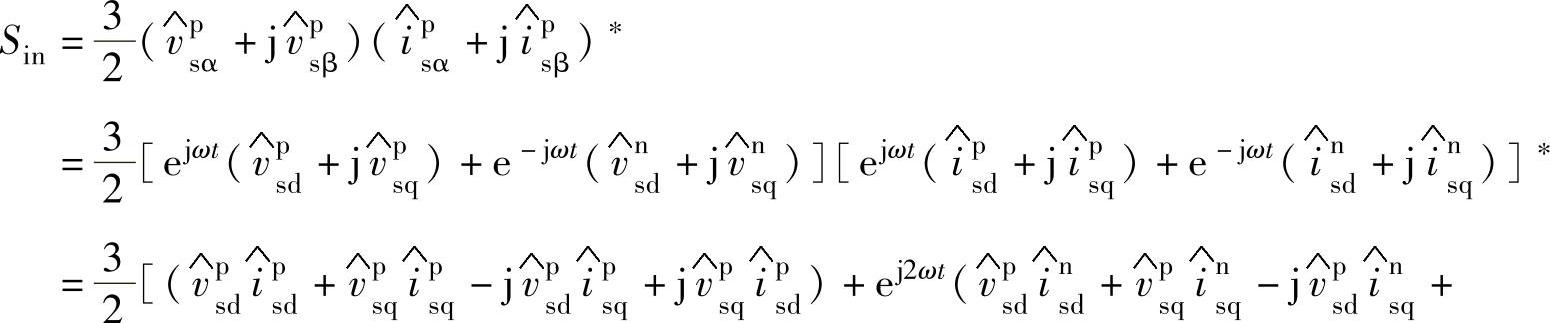
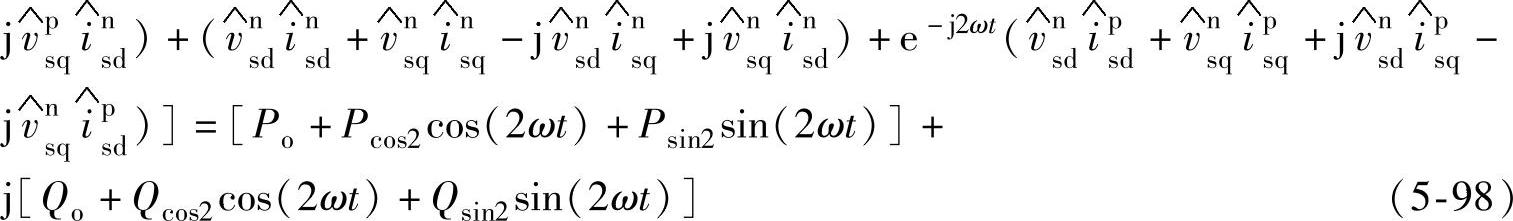
根据式(5-98),当整流器输入电压、电流均不对称时,PWM整流器网侧输入功率存在有功功率和无功功率,而有功功率和无功功率均存在平均输入功率以及相应的工频的两倍频脉动量。需要指出的是,由于三相三线整流器不存在零序电流通路,三相四线整流器的零序电流分量控制目标为零,因此这里不考虑整流器零序电压和电流的影响,以三相三线整流器电路推导电网电压不平衡时整流器输入有功和无功功率分布为

PWM整流器网侧输入有功功率和无功功率表达式如式(5-99)所示,式(5-99)中,Po、Qo表示整流器网侧输入平均有功功率和平均无功功率,Pcos2、Psin2、Qsin2、Qcos2表示电网电压和输入电流不平衡时整流器网侧输入有功功率和无功功率的两倍频脉动量。根据式(5-99),电网电压不平衡时,不同的整流器输入电流将会导致不同的整流器输入功率情况。当整流器网侧输入有功功率存在两倍频脉动量时,整流器直流电压也必将存在两倍频脉动成分。整流器直流电压和开关侧直流母线电流可以表示为
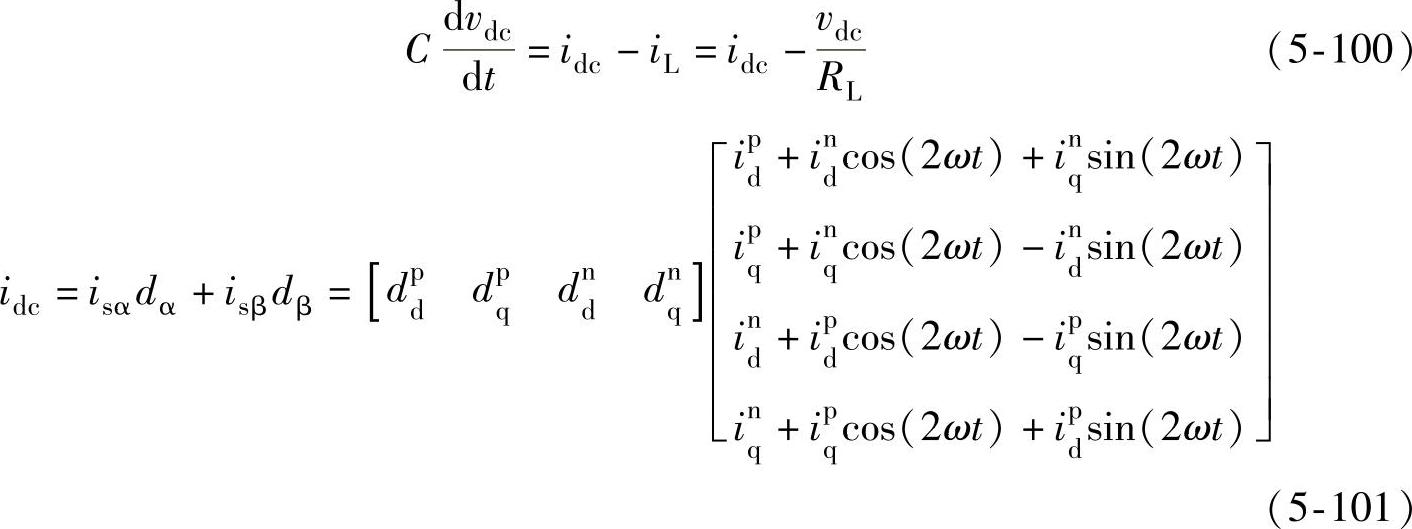
根据式(5-101),整流器网侧电流不平衡时,开关侧直流母线电流含有2次脉动量,整流器直流电压也必将存在两倍频脉动成分。结合式(5-97),整流器直流电压的两倍频脉动将会引起整流器输入电流的2次脉动,结合式(5-101),整流器输入电流2次脉动又将引起开关侧直流电流和直流母线电压4次脉动,如此反复,在电网电压和输入电流不平衡时,直流电压将会包含2、4等偶次谐波分量。为了控制整流器直流侧电压不含有2次谐波,必须使式(5-99)中有功脉动分量幅值Pcos2、Psin2为0。
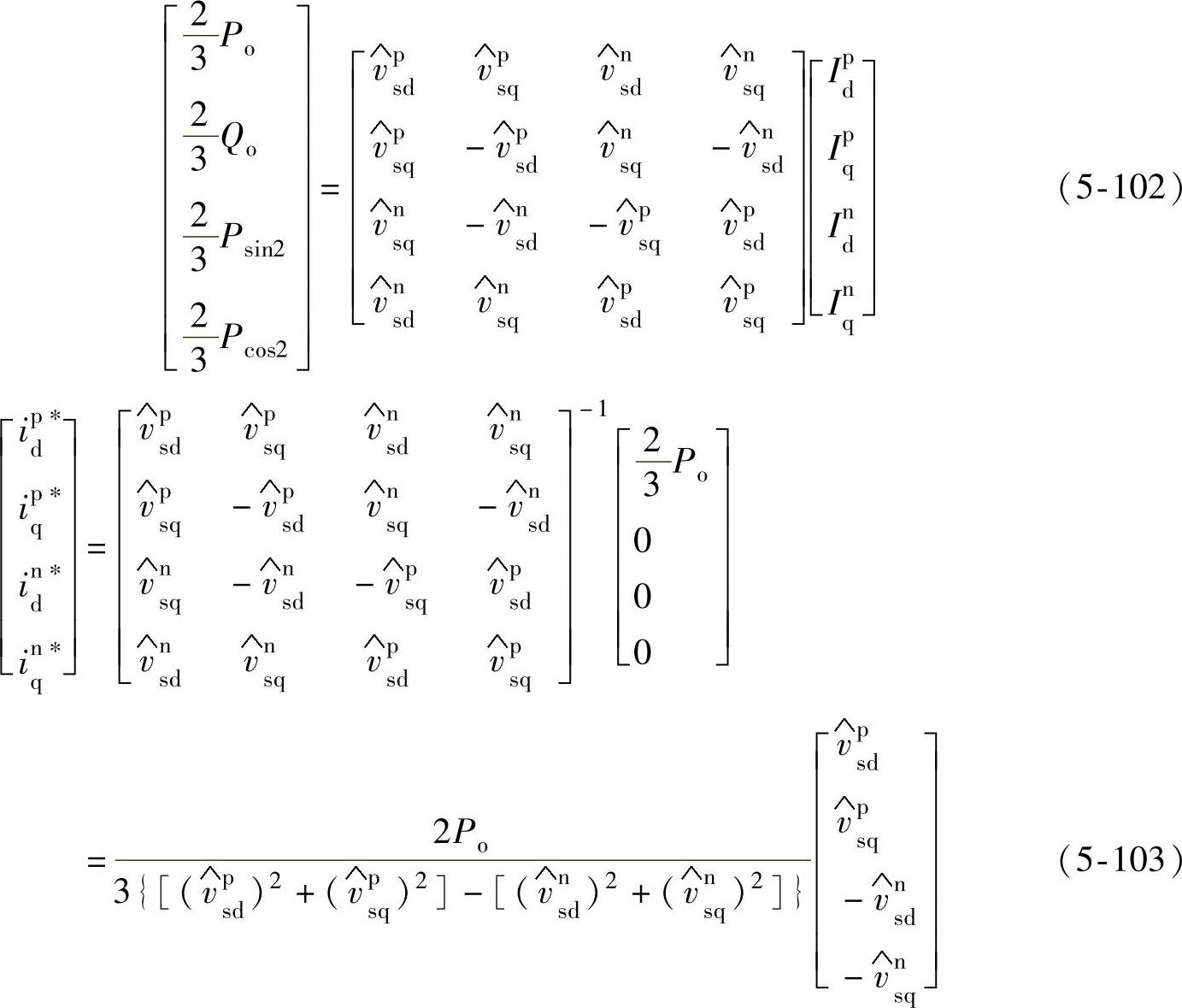
以图5-40中电压调节器输出Po*代入式(5-103),即可得到整流器正序和负序电流基准。以式(5-103)得到的整流器正序和负序电流基准进行电流控制,可以确保整流器直流侧电压无2次脉动,但整流器网侧电流存在负序分量。
在某些情况下,对整流器控制的首要目标主要不是直流侧电压稳定,而是交流侧电流对称,则整流器网侧电流基准为

此时,整流器网侧输入功率为
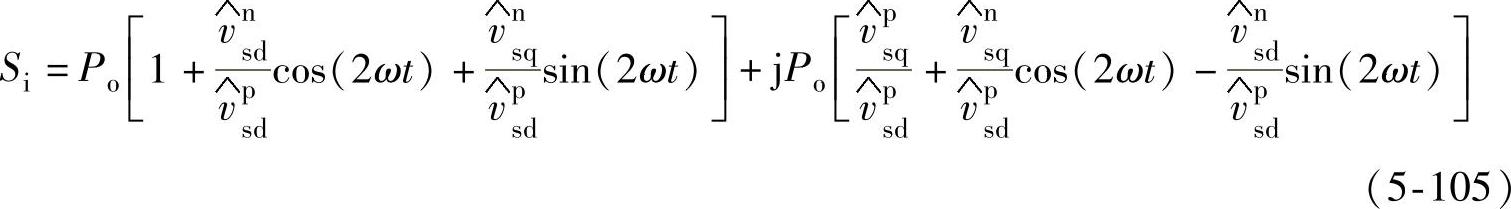
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




