根据5.1.1节的分析,通过调节整流器开关管侧调制电压的幅值和相位,可以调节整流器网侧输入电流的功率因数稳定在正负1之间的任何数值,这是基于整流器一相桥臂的工作情况得到的,在实际控制中,整流器的三相开关管侧调制电压要分别进行计算。如果可以把整流器三相的电压、电流标量用一个矢量来表示,就可以对三相的控制进行综合处理。为了把三相电网电压标量用一个统一的合成量表示,按照Clark变换定义,引入电压空间矢量,为
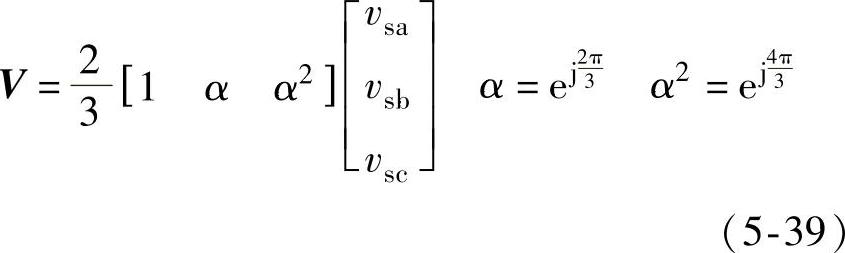
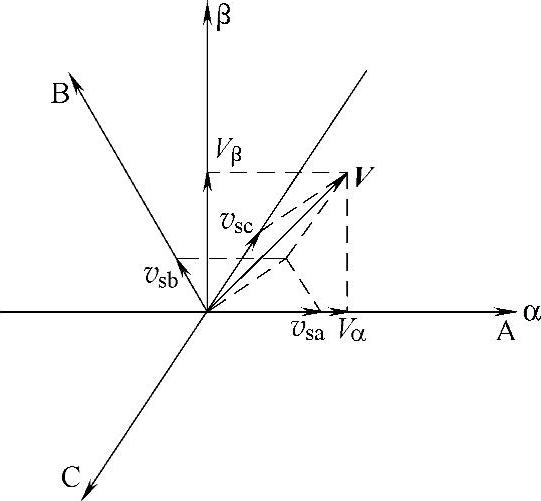
图5-11 三相电压标量到电压空间矢量的变换
式中,V为电压空间矢量,它在复平面上的投影为一个复数,存在实部和虚部,定义实部所在轴为α轴,虚部所在轴为β轴,同时电压空间矢量V还存在零轴分量,如图5-11所示。Clark变换矩阵如下式所示:
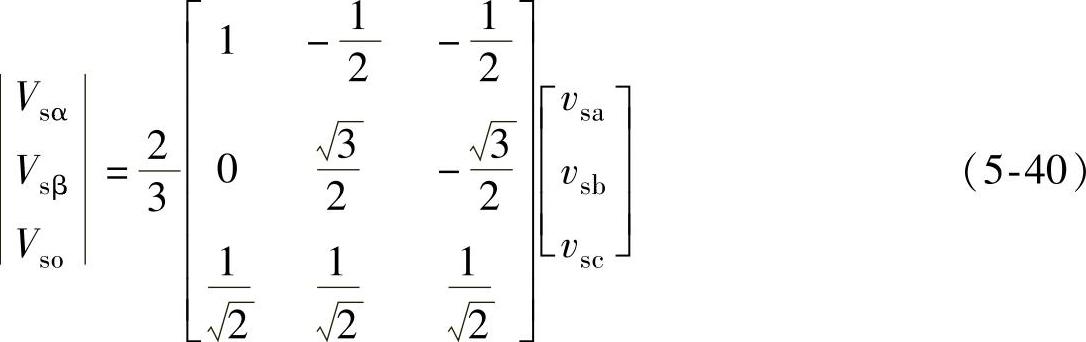
根据式(5-39),电压空间矢量V与三相电网电压瞬时值存在一一对应关系,而三相电网电压可以分解为正序、负序和零序分量,如式(5-14)~式(5-16)所示。这里也可以把电压空间矢量V相应地分解为正序分量Vp、负序分量Vn和零序分量V0,如式(5-41)、式(5-42)所示。
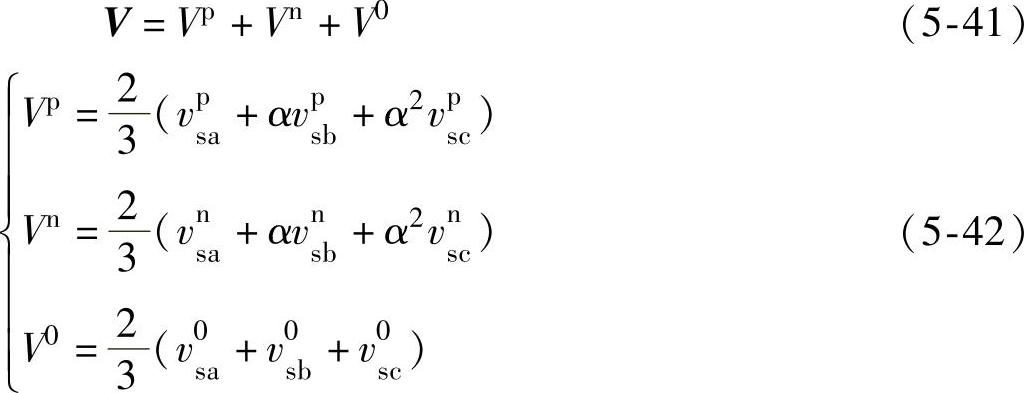
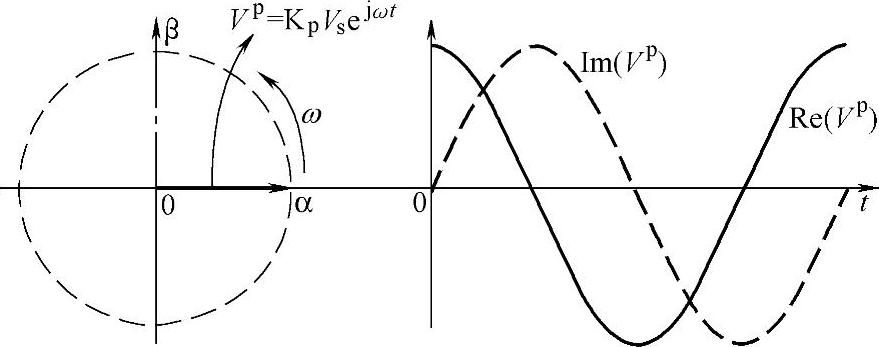
图5-12 空间矢量正序分量Vp运行轨迹
式中,电压空间矢量零序分量V0在空间矢量静止坐标平面上的投影为0。电压空间矢量正序分量Vp在空间矢量静止坐标平面上的轨迹如图5-12所示。结合电网电压正序分量瞬时值表达式(5-14),电压空间矢量轨迹在矢量静止坐标平面α轴和β轴的投影如式(5-43)所示。由图5-12可得,对应三相电网电压瞬时值正序分量余弦函数,电压空间矢量正序分量Vp在矢量静止坐标平面上以角速度ω逆时针匀速旋转,旋转轨迹为圆形,旋转矢量模长即圆轨迹的半径为电网相电压峰值,Vp在α轴和β轴的投影分别为时间轴上幅值为矢量模长的余弦和正弦函数,Vαp在时间轴上的相位等于电网电压正序分量a相相位。
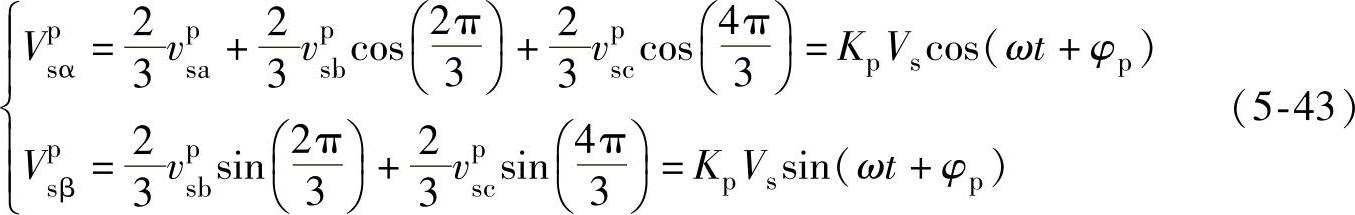
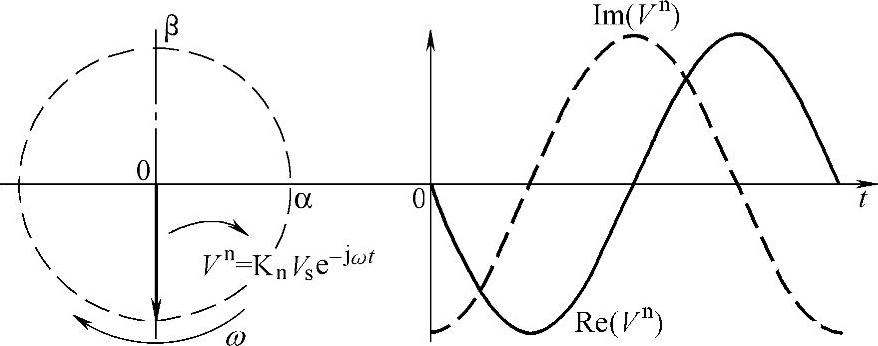
图5-13 空间矢量负序分量Vn运行轨迹
式(5-42)中,矢量负序分量Vn在空间矢量平面上如图5-13所示,其在α轴和β轴的投影如式(5-44)所示。由图5-13可得,对应三相电网电压负序分量余弦函数,Vn在矢量平面上以角速度ω顺时针匀速旋转,旋转轨迹为圆形,圆轨迹的半径为负序相电压峰值,Vn在α轴和β轴的投影分别为时间轴上幅值为矢量模长的余弦和正弦函数,Vnα等于电网电压负序分量a相相位。
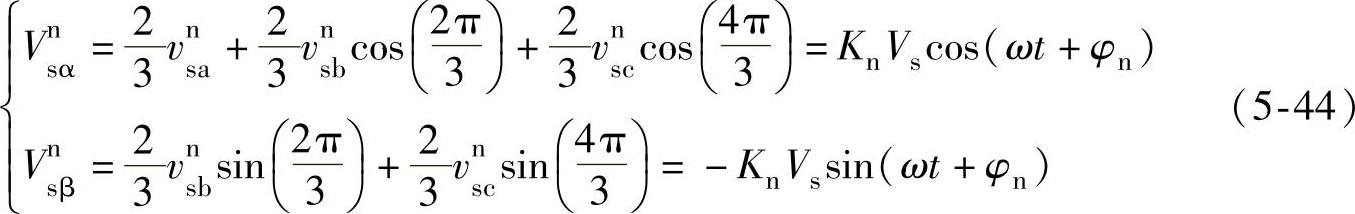
结合正序和负序电压空间矢量,式(5-41)中总的电压空间矢量V在空间矢量静止坐标平面上如图5-14所示。由图5-14可得,V在矢量平面上旋转轨迹为椭圆形,V的实部和虚部标量分别为时间轴上幅值为正负序矢量模长方均根值的余弦和正弦函数,V在矢量平面上的旋转方向取决于电网电压的对称性,当电网电压正序旋转矢量模长大于负序旋转矢量模长,V在矢量平面上逆时针旋转,当电网电压正序旋转矢量模长小于负序旋转矢量模长,V在矢量平面上顺时针旋转。
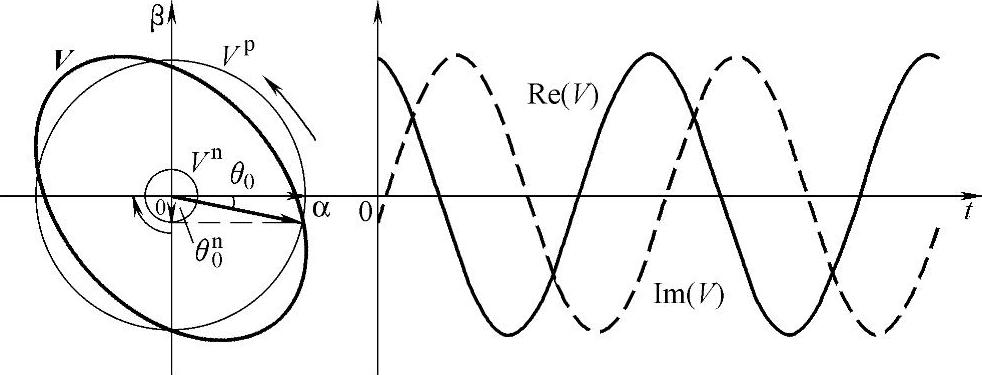
图5-14 空间矢量V运行轨迹
根据上述分析,时间轴上的三相电网电压标量跟空间矢量静止坐标平面上的旋转电压空间矢量存在一一对应关系,任一时刻的三相电网电压瞬时值对应唯一一个固定模长和固定旋转角度的空间电压矢量,同理,任一模长跟任一旋转角度的空间矢量电压也对应唯一的一组三相电网电压标量,这样就可以把三相标量的问题归结到一个旋转矢量上进行处理。
基于同样的变换方法,可以将三相标量的PWM整流器状态方程变换到α、β静止坐标平面上。Clark逆变换矩阵如下式所示:
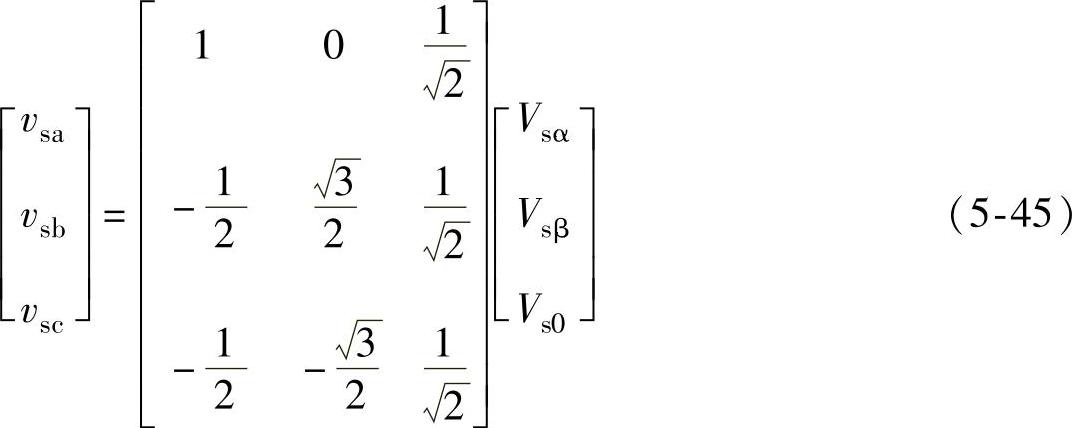
结合Clark变换式(5-40)和逆变换式(5-45),对式(5-6)所示的三相三线PWM整流器状态方程进行推导,可得
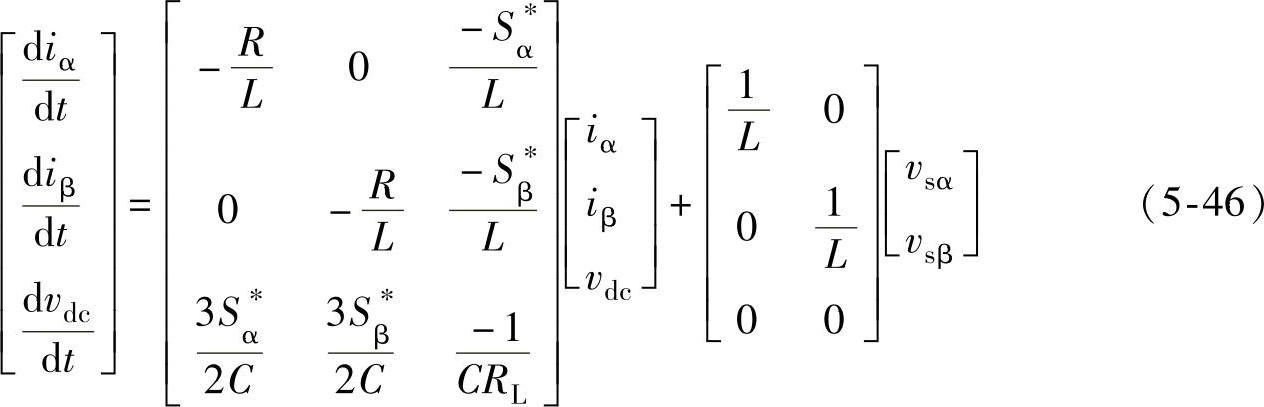
从式(5-46)可以看出,三相三线PWM整流器电网电压零序分量不会影响整流器输入电流和输出电压。式(5-46)中,iα、iβ为ia、ib、ic变换至αβ静止坐标系下的值;Sα*、Sβ*为Sa*、Sb*、Sc*变换至αβ静止坐标系下的值;vsα、vsβ为vsa、vsb、vsc变换至αβ静止坐标系下的值。引入开关周期平均算子,可以得到三相三线PWM整流器在αβ静止坐标系下的平均状态空间模型,即
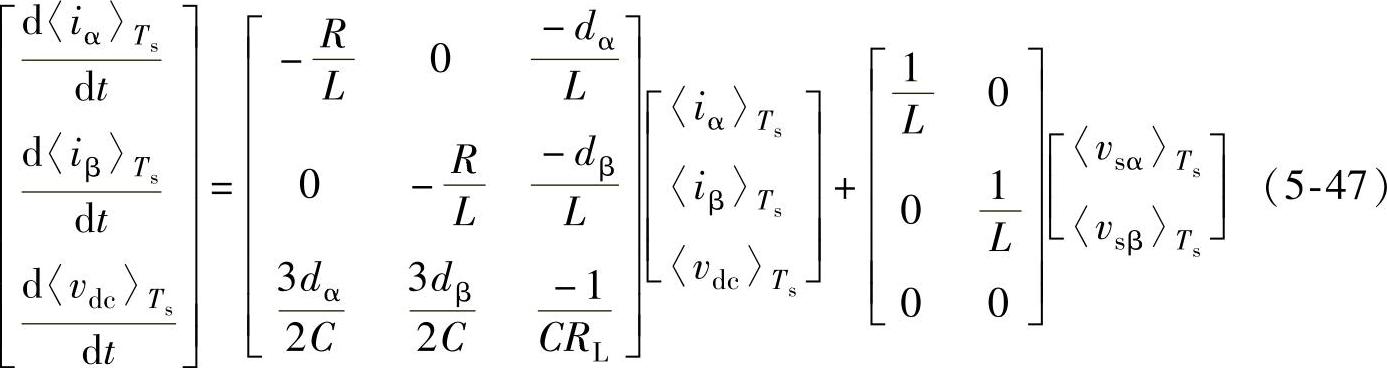
根据式(5-47)可以得到三相三线PWM整流器开关周期平均模型的等效电路,如图5-15所示。
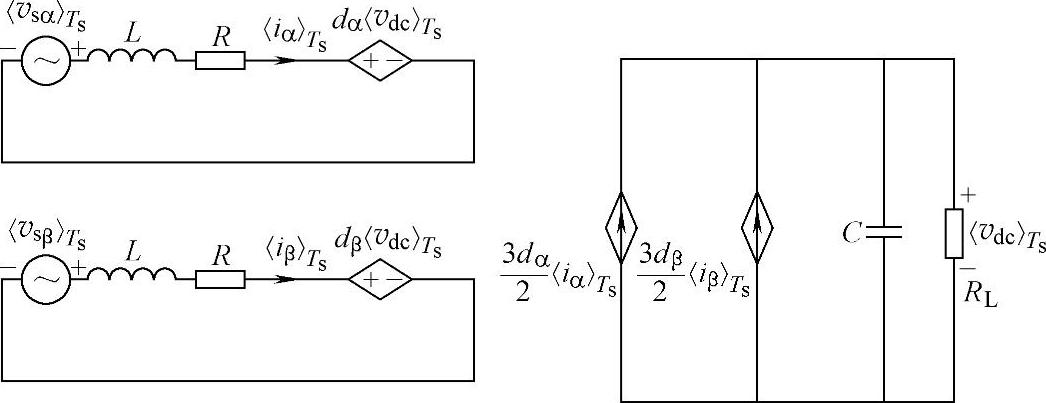
图5-15 三相三线PWM整流器在静止坐标系下开关周期平均模型等效电路1
图5-15所示的三相三线PWM整流器矢量坐标系下开关周期平均模型等效电路1,在电网电压不对称条件下同样适合。式(5-47)中,整流器三相桥臂开关占空比在α、β坐标系下表示为

需要指出的是,根据式(5-48)得到的占空比只在数学意义上成立,在实际变换器开关管控制中,占空比为负值是没有物理意义的,实际的三相三线整流器占空比在电压空间矢量坐标系下如何得到将在后面给出。
把式(5-48)代入式(5-47),得到

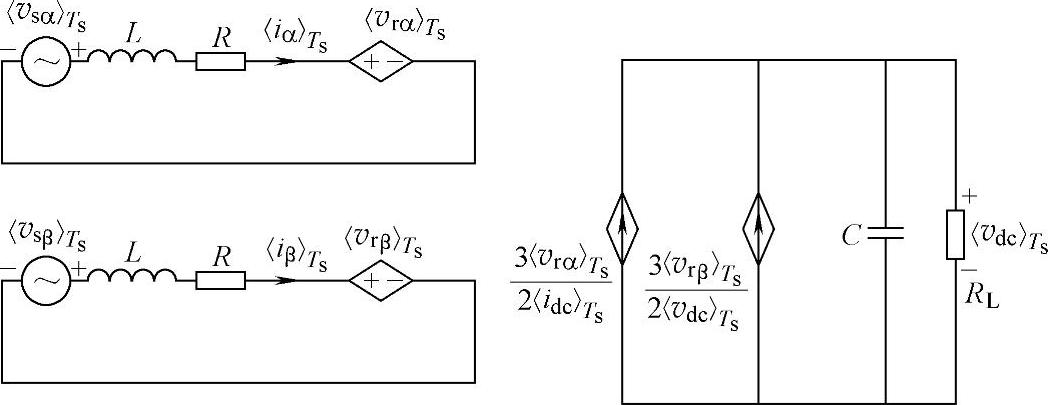
图5-16 三相三线PWM整流器在静止坐标系下开关周期平均模型等效电路2
根据式(5-49)可以得到三相三线PWM整流器的大信号平均模型等效电路2,如图5-16所示,由于式(5-49)表示的基于平均算子的状态空间模型适用于整个工频周期,因此如果只讨论工频情况,可以得到(https://www.xing528.com)
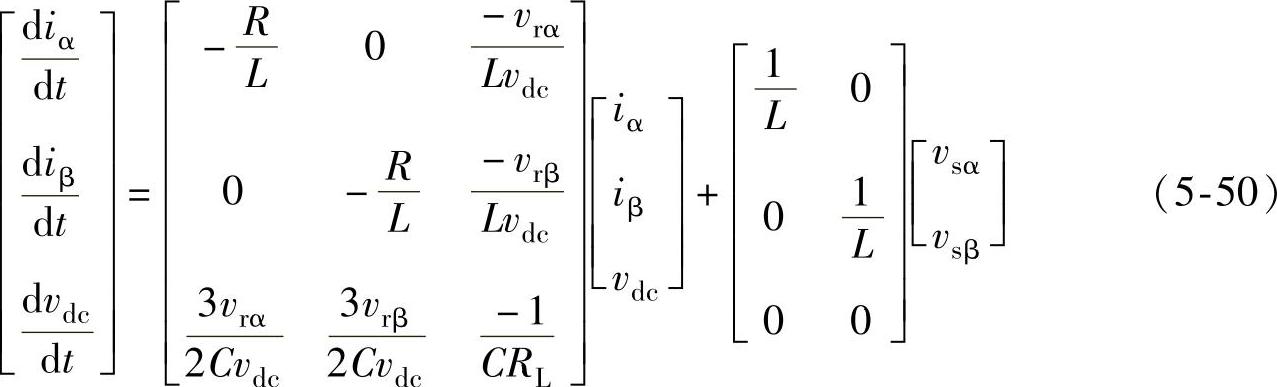
根据式(5-50),得到三相三线PWM整流器在矢量坐标系下的工频等效电路,如图5-17所示。在空间矢量坐标系下,考虑电感寄生电阻时三相三线整流器电压电流稳态空间矢量图如图5-18所示。
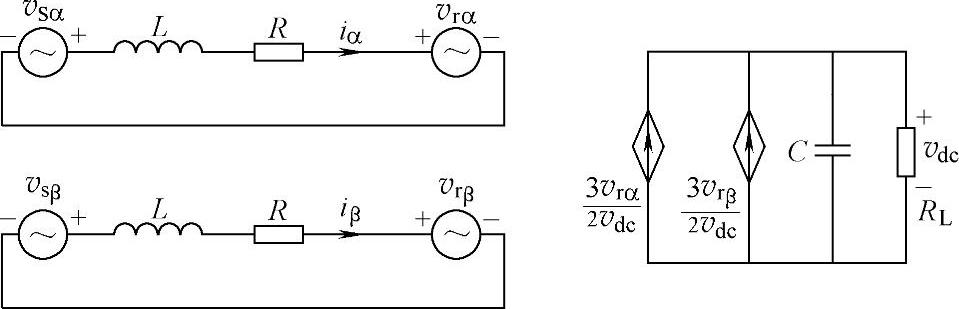
图5-17 三相三线PWM整流器在矢量坐标系下的工频模型
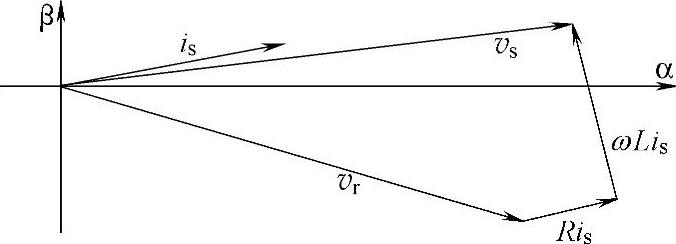
图5-18 考虑电感寄生电阻时三相三线整流器电压电流稳态空间矢量图
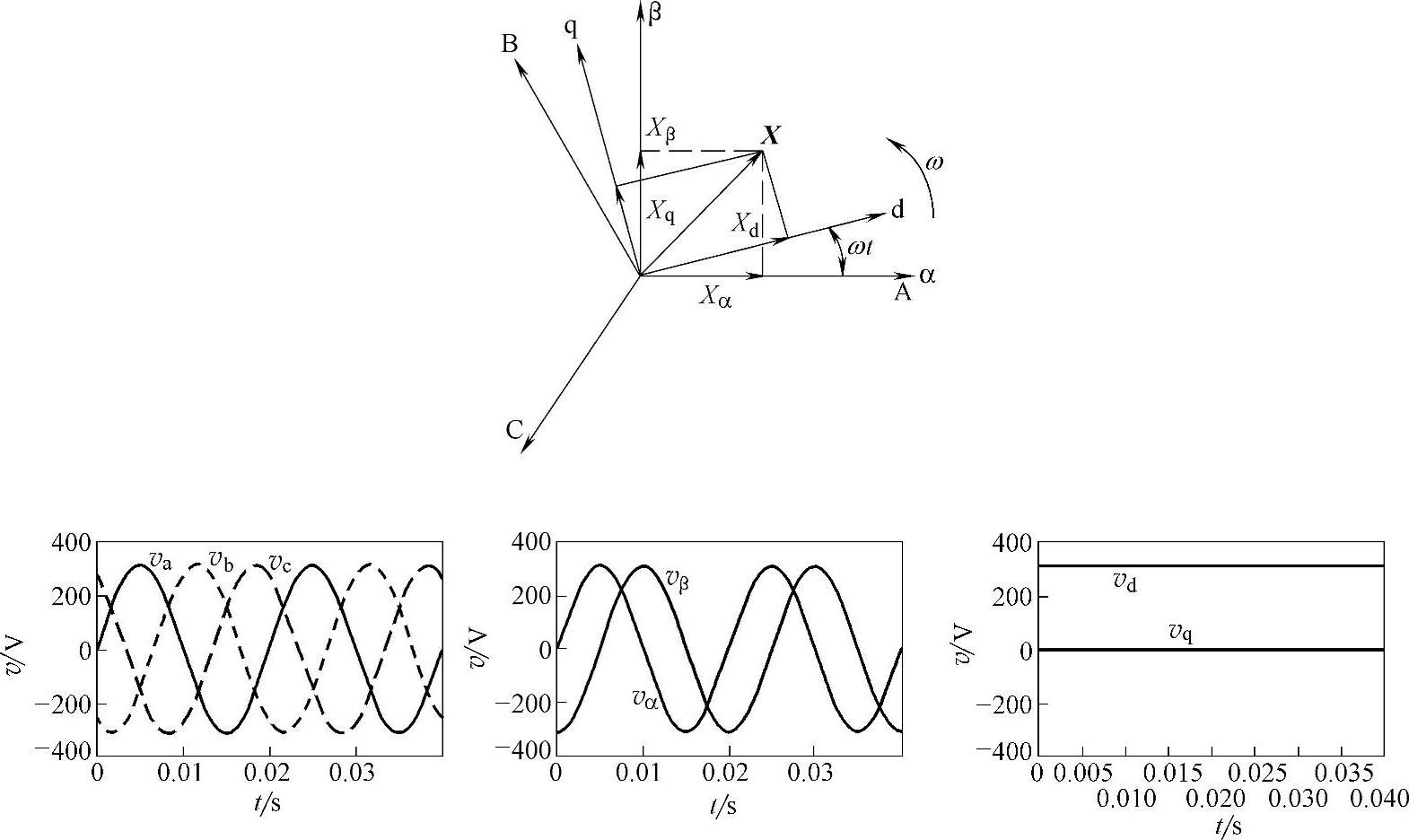
图5-19 三相电压标量到αβ静止坐标系和dq旋转坐标系之间变换曲线
对于三相平衡系统,电网电压经Park变换后,得到的空间矢量长度不变。如果让α、β坐标轴也以与电压空间矢量同样的角频率逆时针旋转,那么在旋转坐标系中看,由Park变换得到的电压空间矢量是静止的,空间矢量在旋转坐标轴上的分量也是静止的直流量。所以,如果进一步将式(5-46)表示的静止坐标系下整流器状态方程变换到以电网角频率ω逆时针旋转的同步dq0坐标系模型中,那么电网电压正弦信号就变成了常数。
三相交流电压标量到αβ静止坐标系和dq旋转坐标系之间的变换曲线如图5-19所示。静止与旋转坐标系间的变换式为

式中
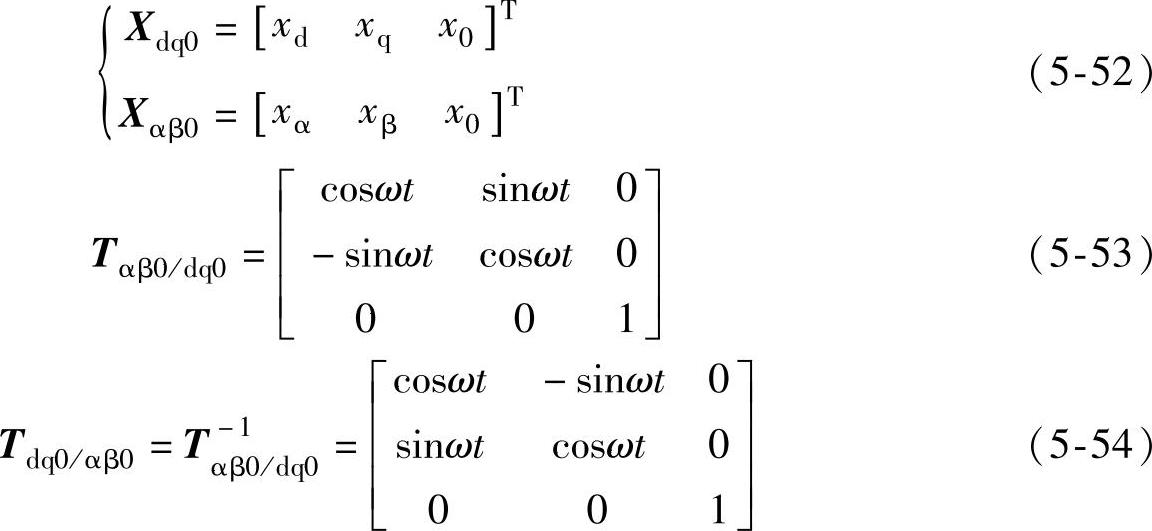
由于式(5-46)已经证明电网电压零序分量不会影响三相三线整流器输入电流和输出电压,这里的变换不再考虑零序输入电压。前面静止坐标系之间变换矩阵是常数矩阵,故状态变量的导数不改变。而静止和旋转坐标系间的变换矩阵内的元素本身也是时间的变量,所以在对状态变量的导数进行旋转变换时,不能简单地认为α、β轴电流的导数经旋转变换就是d、q轴电流的导数。而应按式(5-55)对d、q轴电流求导,得到两个坐标系间电流导数的关系是
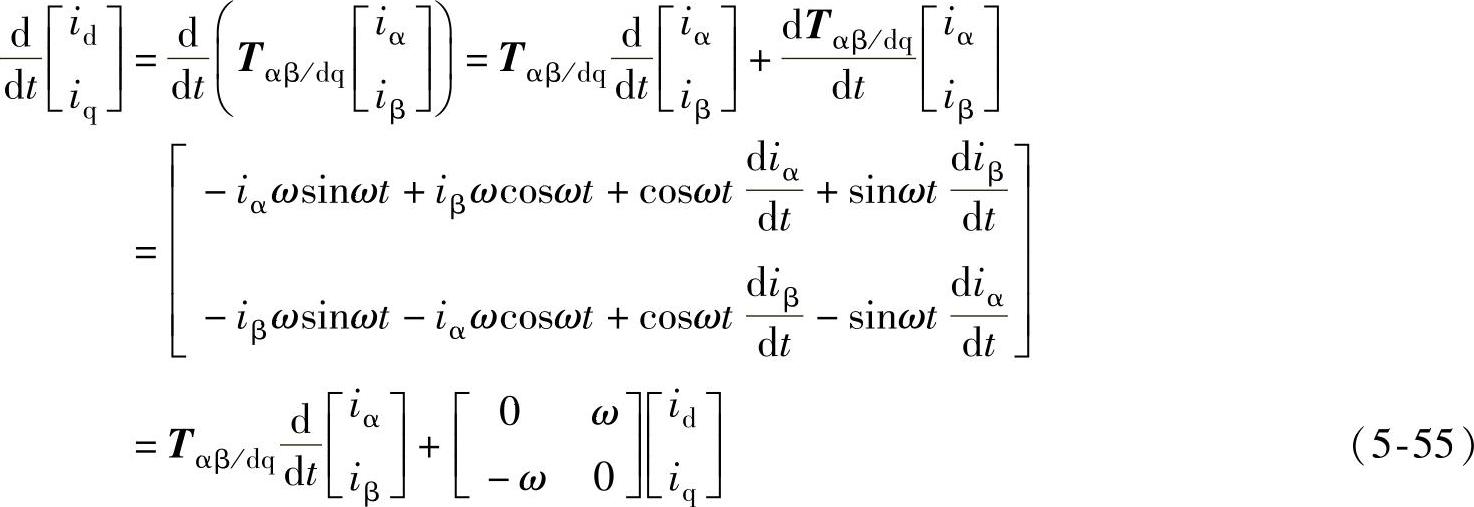
将式(5-51)、式(5-55)应用于式(5-46),得到两相同步坐标系下的整流器模型为
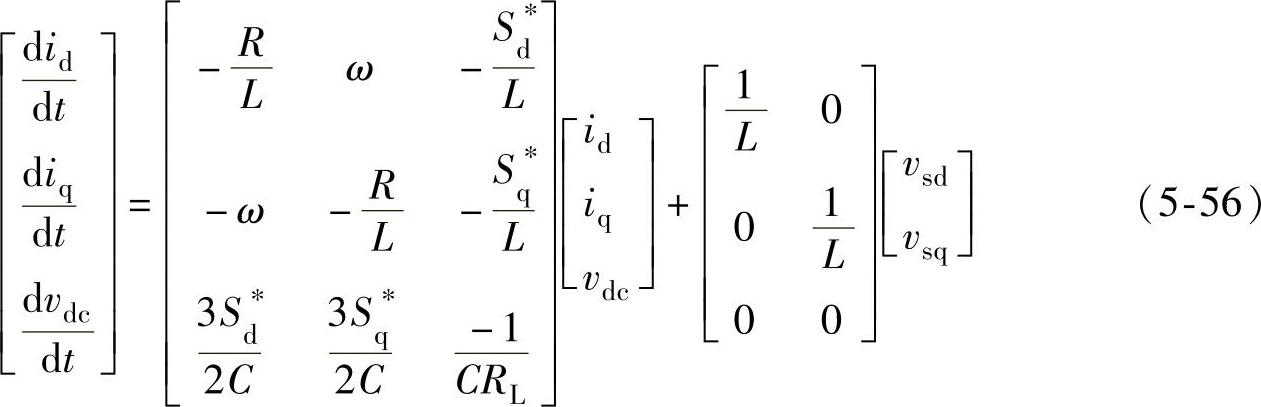
从式(5-56)可以看出,三相三线PWM整流器电网电压零序分量不会影响整流器输入电流和输出电压。式(5-56)中,id、iq为iα、iβ变换至同步旋转坐标系下的值;Sd*、Sq*为Sα*、Sβ*变换至同步旋转坐标系下的值;vsd、vsq为vsα、vsβ变换至同步旋转坐标系下的值。引入开关周期平均算子,可以得到三相三线PWM整流器在dq同步旋转坐标系下的平均状态空间模型为
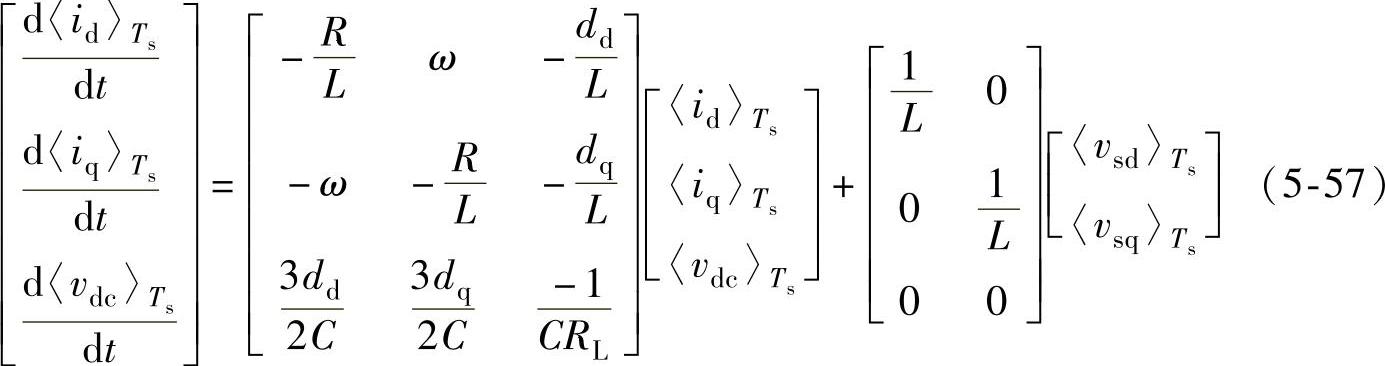
根据式(5-57),可以得到三相三线PWM整流器开关周期平均模型的等效电路,如图5-20所示。图中的各符号和式(5-57)的相同。比较静止坐标系和旋转坐标系下的模型可以发现,在αβ静止坐标系下,α、β轴电流之间相互独立,不存在耦合关系;在dq同步旋转坐标系下,d、q轴电流之间不独立,存在耦合关系,这种现象与旋转电机正好相反,这是由于电路本身是静止电路,所以在静止两相坐标系中不存在耦合,而变换至旋转坐标系下,由于电感的作用,在d、q两轴之间产生耦合,d、q任一轴的占空比变化都会同时引起d、q轴的输入电流变化。为了简化控制环路设计,在设计控制系统时,有必要进行电流环解耦,以使系统的静动态性能达到最优。
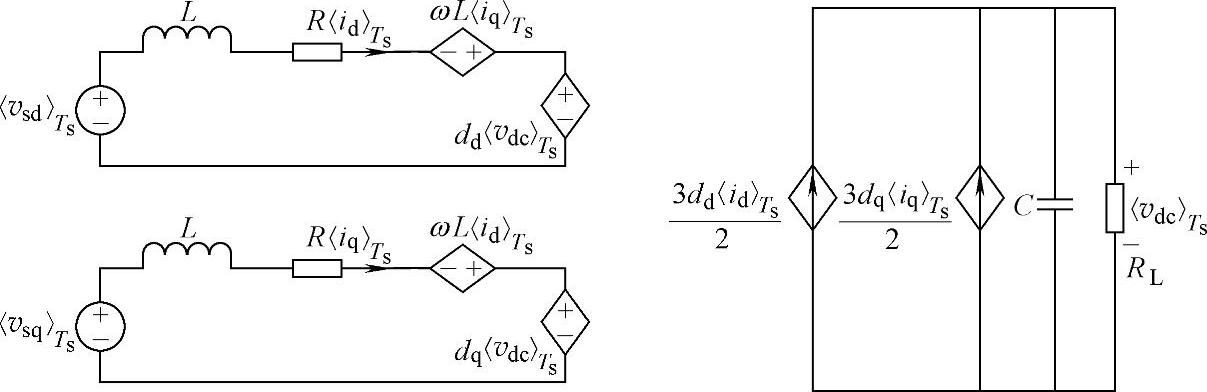
图5-20 三相三线PWM整流器在同步旋转坐标系下开关周期平均模型等效电路
图5-20所示的三相三线PWM整流器在同步旋转坐标系下开关周期平均模型的等效电路,在电网电压不对称条件下同样适合。式(5-57)中,整流器三相桥臂开关占空比在同步旋转坐标系下定义为

需要指出的是,根据式(5-58)得到的占空比只在数学意义上成立,在实际整流器开关调制中,占空比为负值是没有物理意义的,实际的三相整流器占空比在电压空间矢量坐标系下如何得到将在后面给出。
把式(5-58)代入式(5-57),得到

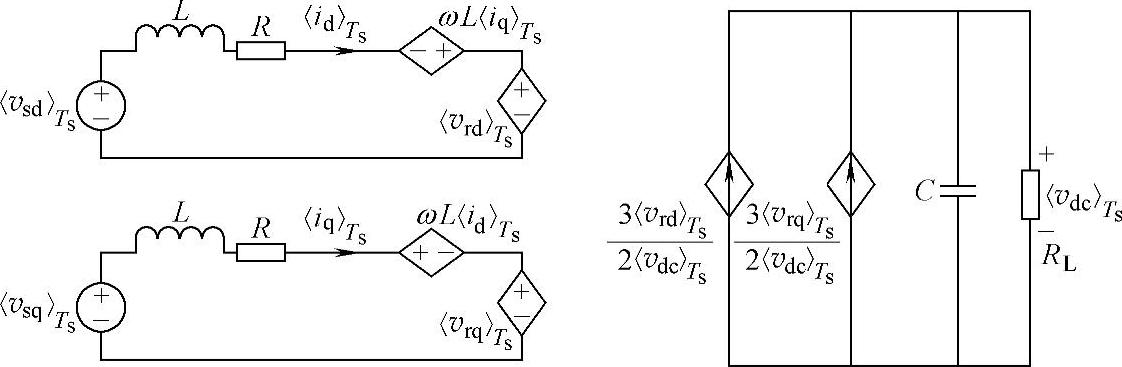
图5-21 三相三线PWM整流器在同步旋转坐标系下的大信号开关周期平均模型等效电路
根据式(5-59),可以得到三相三线PWM整流器在同步旋转坐标系下的大信号开关周期平均模型,如图5-21所示。由于式(5-59)表示的是基于平均算子的状态空间模型,适用于整个工频周期,因此如果只讨论工频情况,可以得到
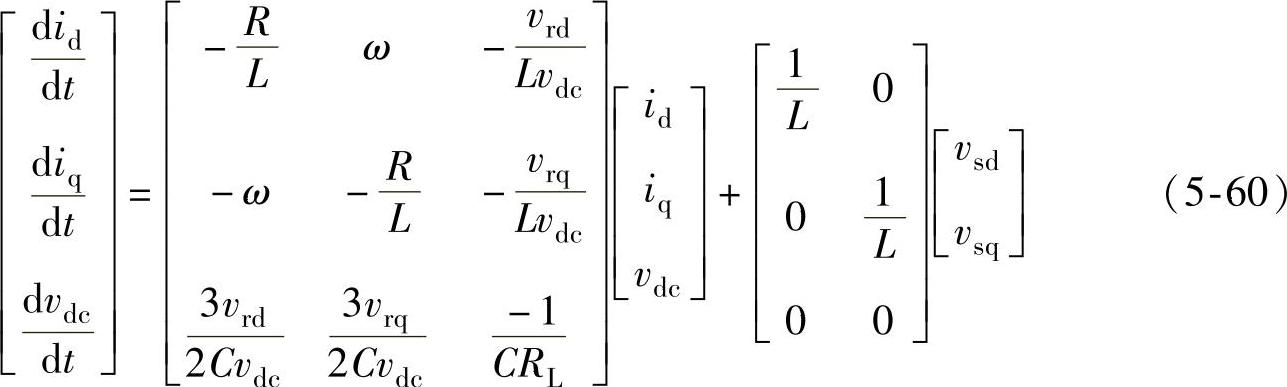
根据式(5-60)得到的三相三线PWM整流器在矢量坐标系下的工频等效电路如图5-22所示,则在空间矢量坐标系下,考虑电感寄生电阻时三相三线整流器电压、电流稳态空间矢量图如图5-23所示。
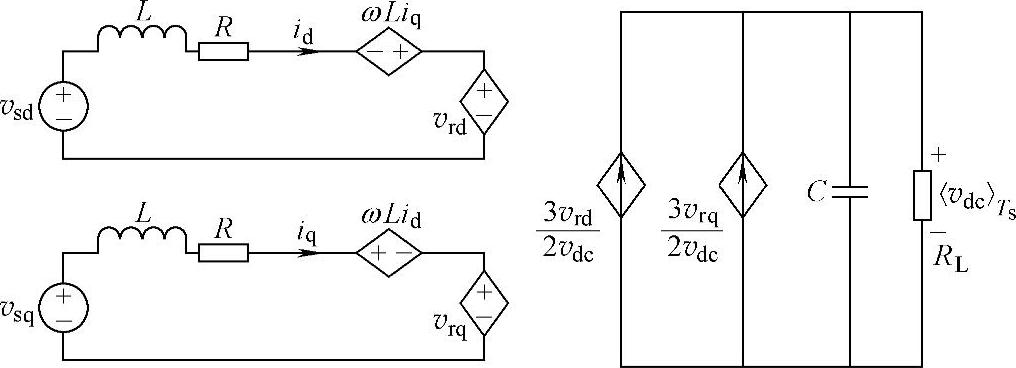
图5-22 三相三线PWM整流器在同步旋转坐标系下的工频模型
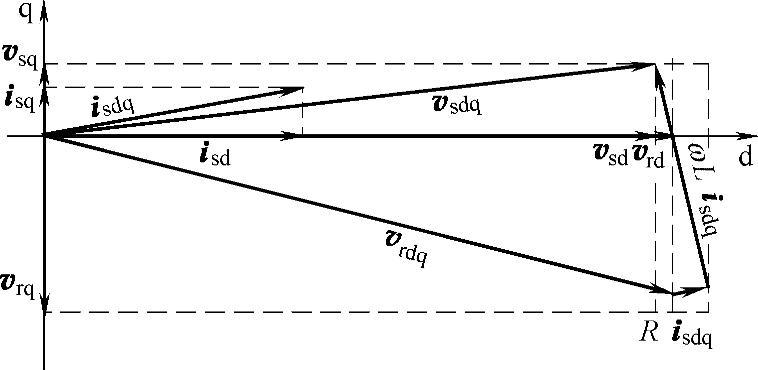
图5-23 考虑电感寄生电阻的电压、电流同步旋转坐标系等效矢量图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




