三相三线PWM整流器工作原理简介

三相三线PWM整流器电路如图5-1所示。图5-1中，V₁～V₆为主开关管，三相电网电压和网侧输入电流瞬时值分别表示为v_sa、v_sb、v_sc和i_a、i_b、i_c，O点为交流电压参考点；L和R表示滤波电感及其寄生电阻和线路电阻值，C表示整流器输出直流滤波电容，i_dc和i_L分别表示开关侧直流母线电流和负载侧直流母线电流，v_dc表示直流母线电压，N点表示直流母线参考点，R_L表示整流器输出负载。设开关管是理想开关器件，可以列出三相三线PWM整流器的基本方程为

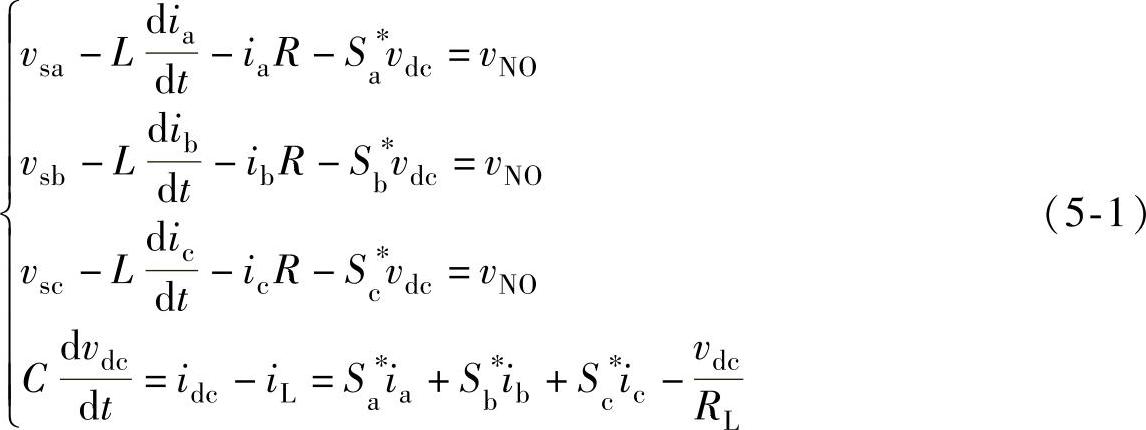
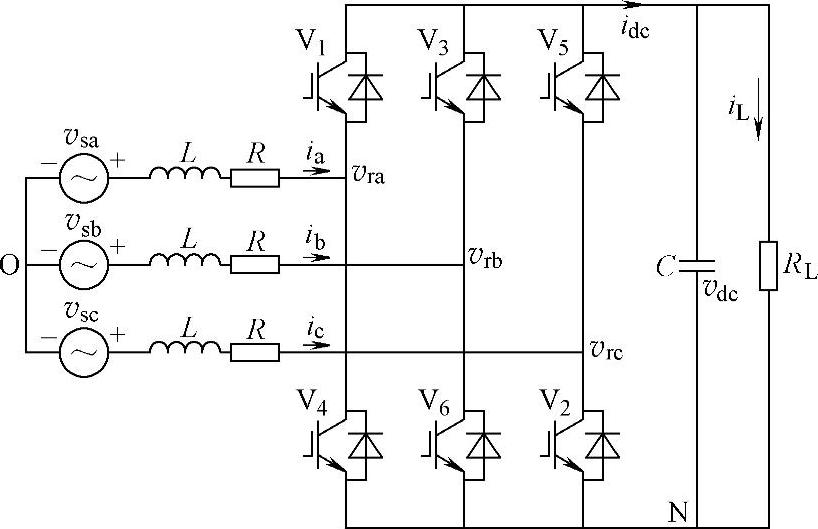
图5-1 三相三线PWM整流器电路原理图

式中，S_a^*、S_b^*、S_c^*分别为三相三线PWM整流器桥臂侧开关函数，S_x^*（x=a，b，c）=1代表对应的桥臂上管导通、下管关断，S_x^*（x=a，b，c）=0代表对应的桥臂下管导通、上管关断；i_dc为整流器的直流侧输出电流；i_L为整流器的直流侧负载电流；v_dc为整流器的输出直流电压。为了得到整流器电感电流状态方程，对式（5-1）中前三式相加，得

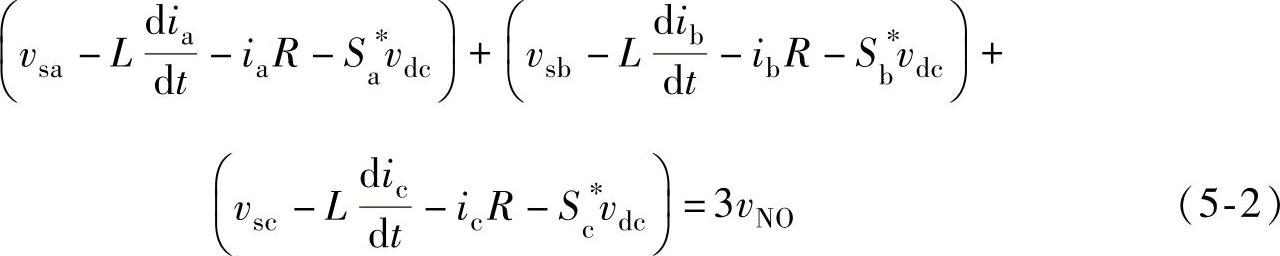
整理上式得到：

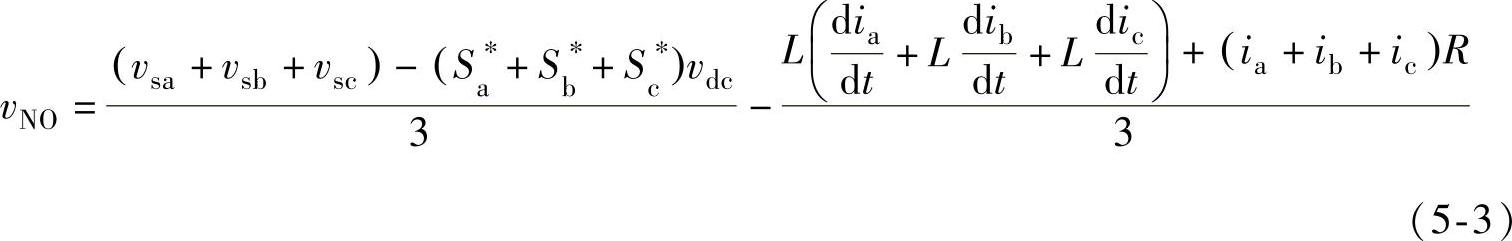
由于在三相三线PWM整流器中，三相网侧输入电流瞬时值之和等于零，即

i_a+i_b+i_c=0 （5-4）

结合式（5-3）和式（5-4）可以得到

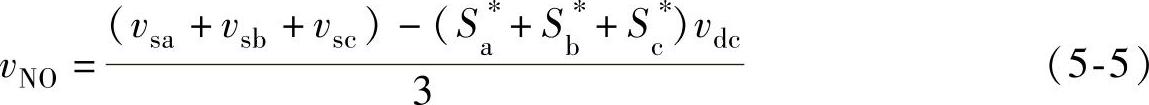
把式（5-5）代入式（5-1）并写成矩阵形式，可以得到三相三线PWM整流器状态方程如下式所示：

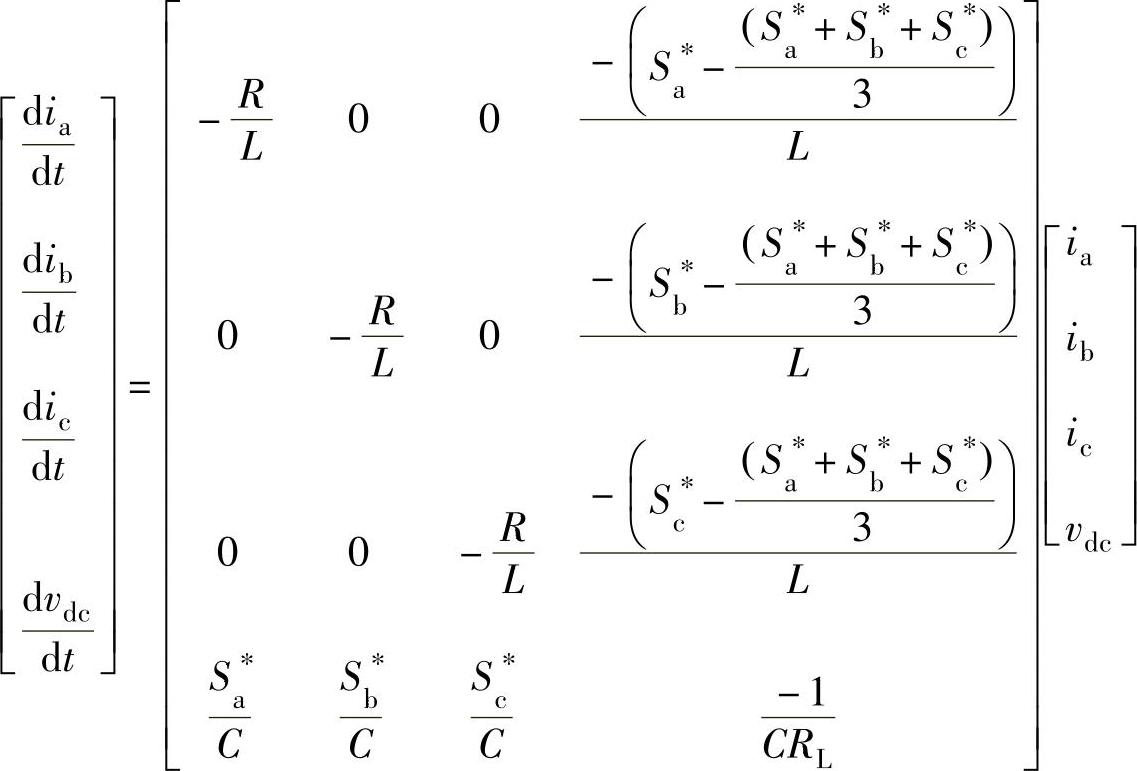
为简化模型，忽略开关频率及其边频带、开关频率谐波及其边频谐波，引入开关周期平均算子

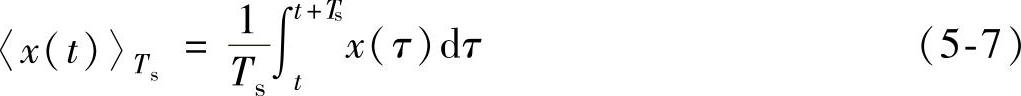
式中，T_s为开关周期。对电压电流进行开关周期平均运算，可以保留原信号低频成分，而滤除开关频率分量、开关频率谐波分量及其边频分量。将开关周期平均算子概念引入三相三线PWM整流器状态方程，可以得到三相三线PWM整流器平均状态空间模型为

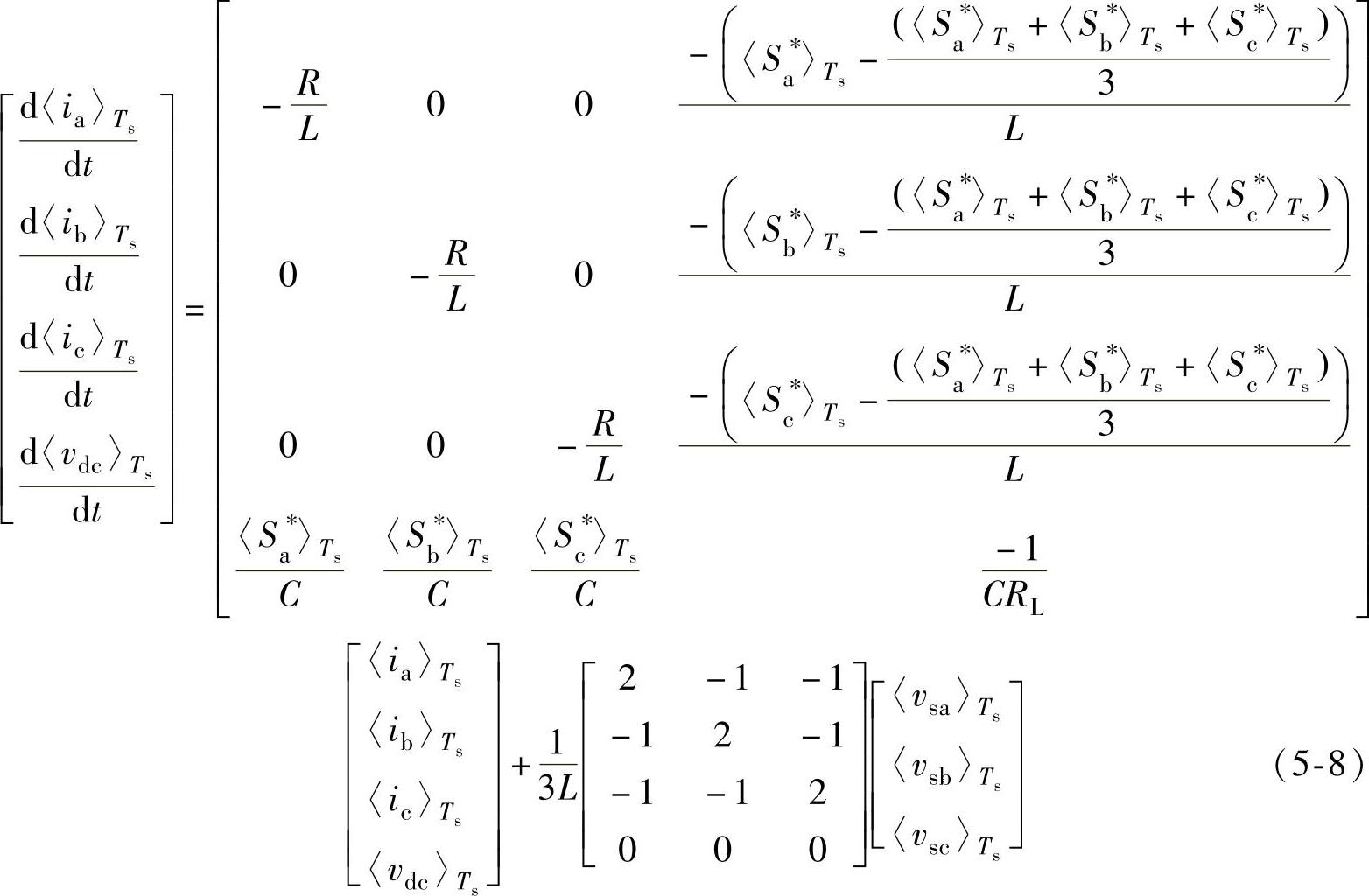
定义整流器三相桥臂开关占空比为

将占空比的表达式（5-9）代入式（5-8），可以得到

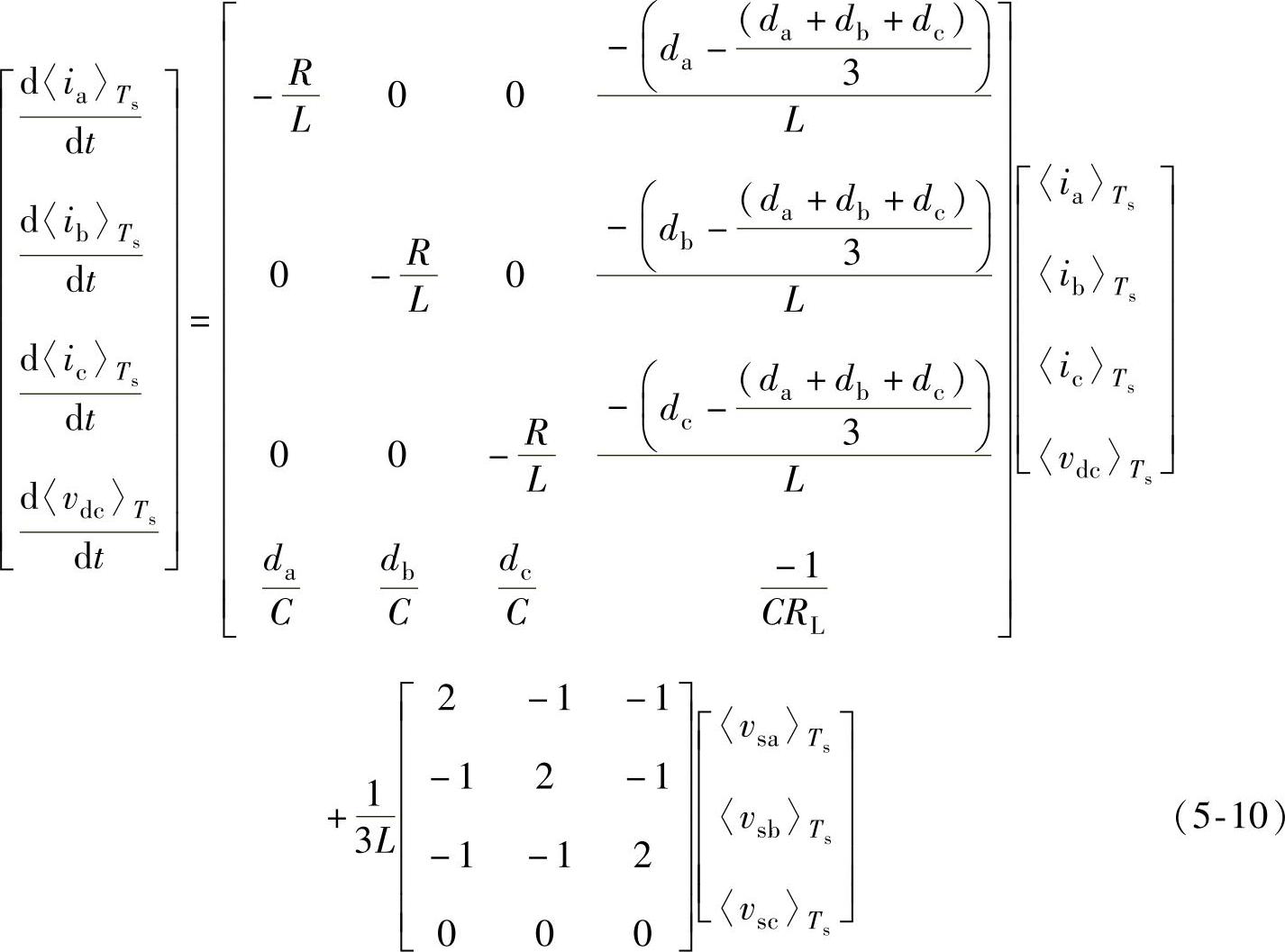
根据式（5-10）可以得到三相三线PWM整流器开关周期平均模型的等效电路，如图5-2所示。

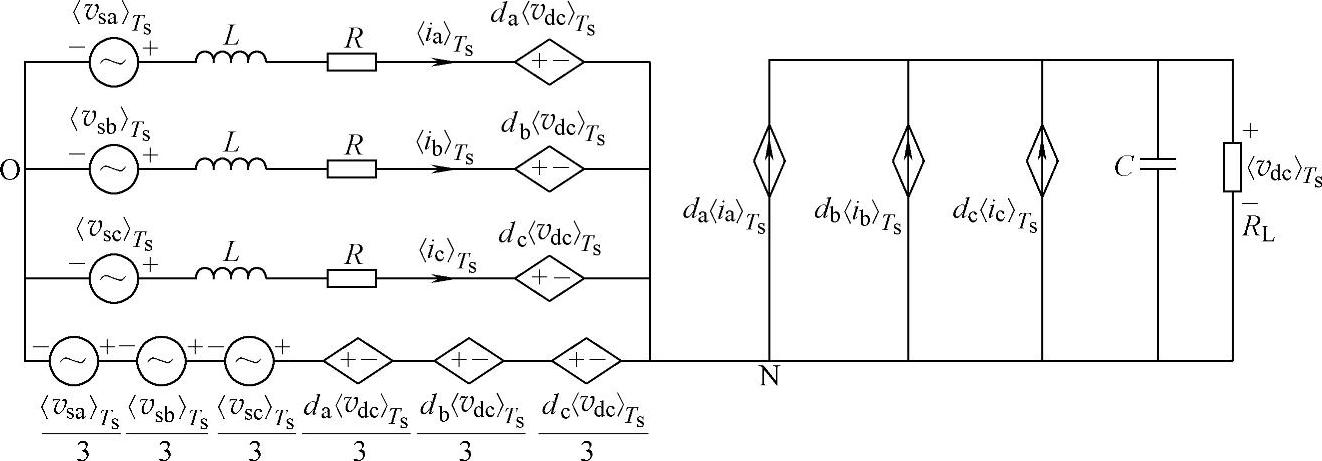
图5-2 三相三线PWM整流器开关周期平均模型的等效电路

图5-2所示的三相三线PWM整流器开关周期平均模型的等效电路中，电网电压参考点O与整流器直流侧参考电位N存在电压差v_NO，即

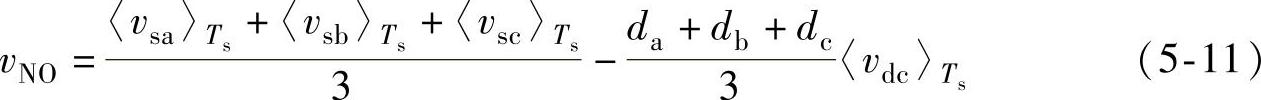
需要指出的是，三相三线PWM整流器中由于不存在零序电流通路，v_NO对电感电流变化不产生影响。

假设只考虑三相电网电压基波分量，则电网电压可表示为

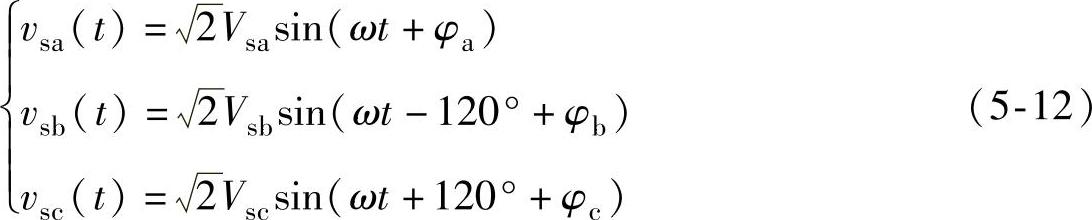
式中，ω=2πf（f表示电网电压频率）；V_sx（x=a，b，c）表示相电压有效值，如图5-3a所示。当三相电压的有效值V_sa≠V_sb≠V_sc或者相移φ_a≠φ_b≠φ_c时，为不对称电网电压，根据电路基本理论，三相不对称交流电网电压基波分量可以分解为对称的基波正序电压分量、基波负序电压分量和基波零序电压分量，如下式所示：

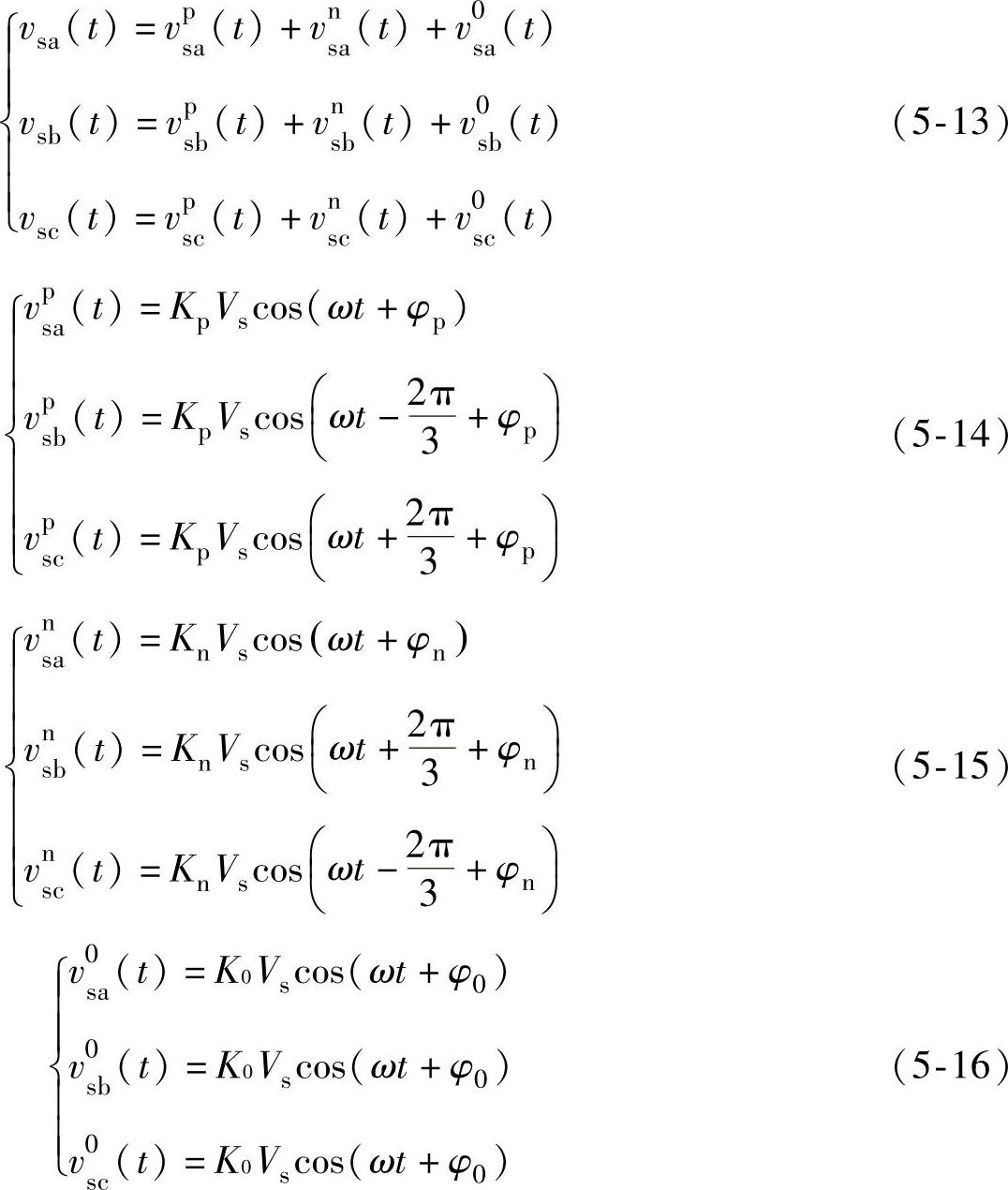
式（5-13）中，三相电网电压中的对称正序电压分量、负序电压分量和零序电压分量分别表示为式（5-14）、式（5-15）和式（5-16）。对于三相正序电压，其相序表示为a相超前b相，b相超前c相，如图5-3b所示；对于三相负序电压，其相序表示为a相滞后b相，b相滞后c相，如图5-3c所示；对于三相零序电压，其a、b、c三相电压分量同相序，如图5-3d所示。

把整流器三相桥臂开关占空比也相应地分解为对称的正序分量、负序分量和零序分量，如下式所示：

图5-3 三相电网电压及其正序、负序、零序分量

把式（5-13）和式（5-17）代入式（5-10），可以得到

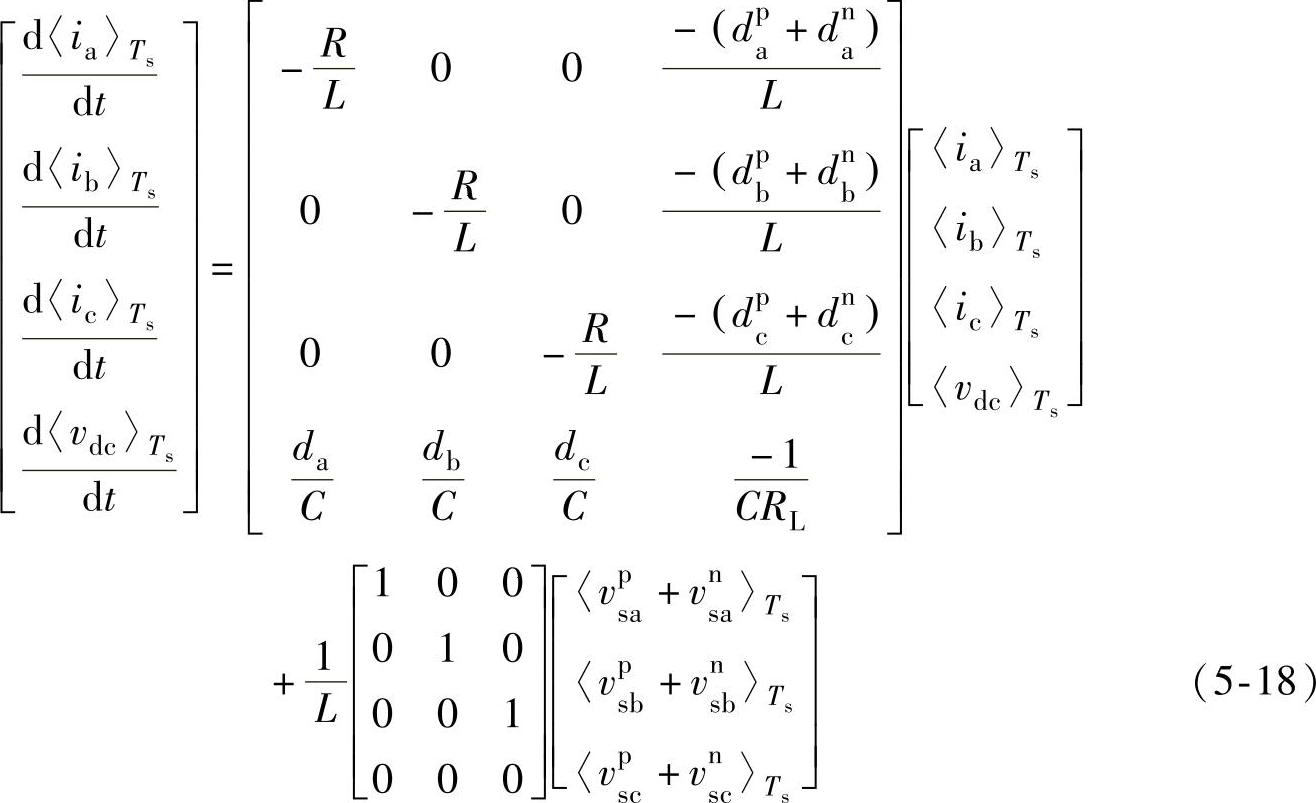
根据式（5-18）可知，在三相三线PWM整流器中，只有电网电压正序分量和负序分量可以对网侧电感电流产生影响，电网电压零序分量不会影响电感电流，整流器三相桥臂开关占空比零序分量同样不会影响电感电流。从式（5-18）得到三相三线PWM整流器开关周期平均模型的等效电路，如图5-4所示。

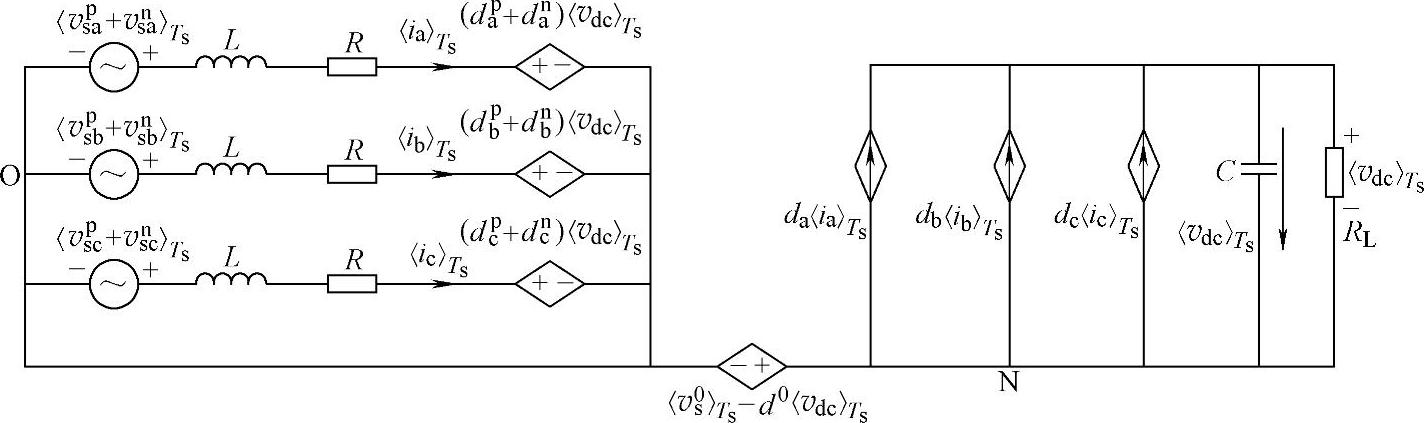
图5-4 考虑电网电压不对称时PWM整流器开关周期平均模型的等效电路

为了分析方便，在图5-4所示的三相三线PWM整流器开关周期平均模型等效电路中，构造了电网电压虚拟参考点O，虚拟参考点O与PWM整流器电网电压实际参考点存在电网电压零序分量电压差。

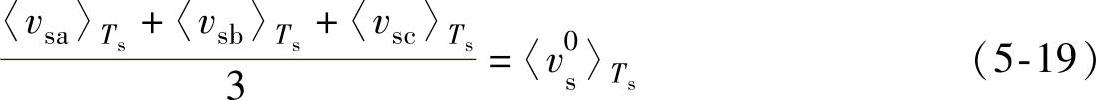
图5-4中，电网电压虚拟参考点O与整流器直流侧参考电位N电压差v_NO表示为

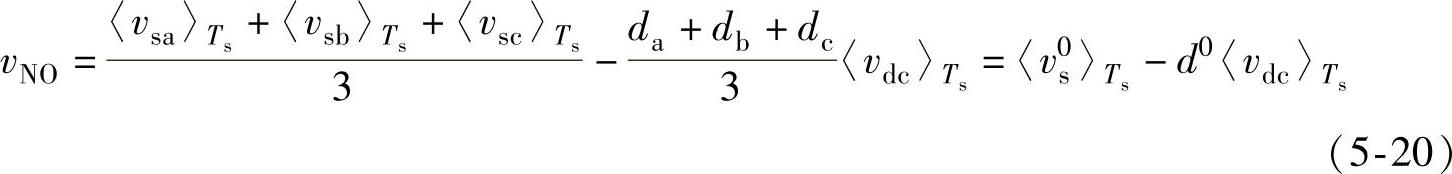(www.xing528.com)

如果采用双极性PWM控制方法对三相三线六开关整流器进行调制，整流器三相桥臂占空比表示为

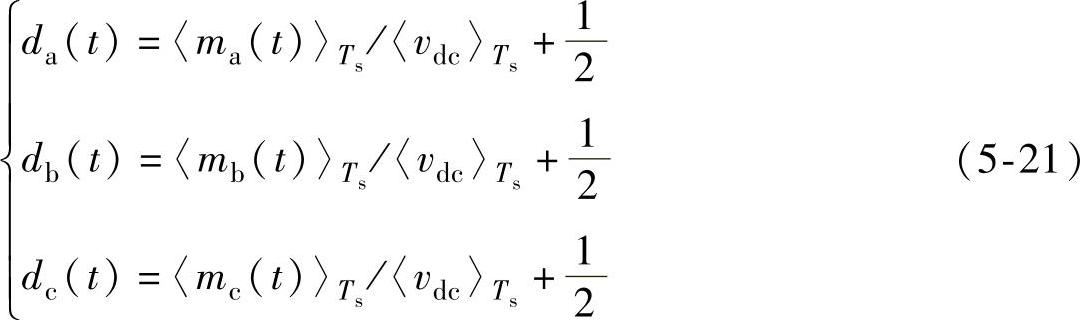
式中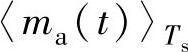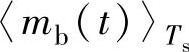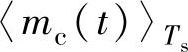，、、为一个开关周期中整流器各相开关调制波电压平均值，调制波形如图5-5所示。

在三相电网电压不平衡的条件下，三相调制波形也相应包含交流正序分量、负序分量和零序分量，如下式所示：

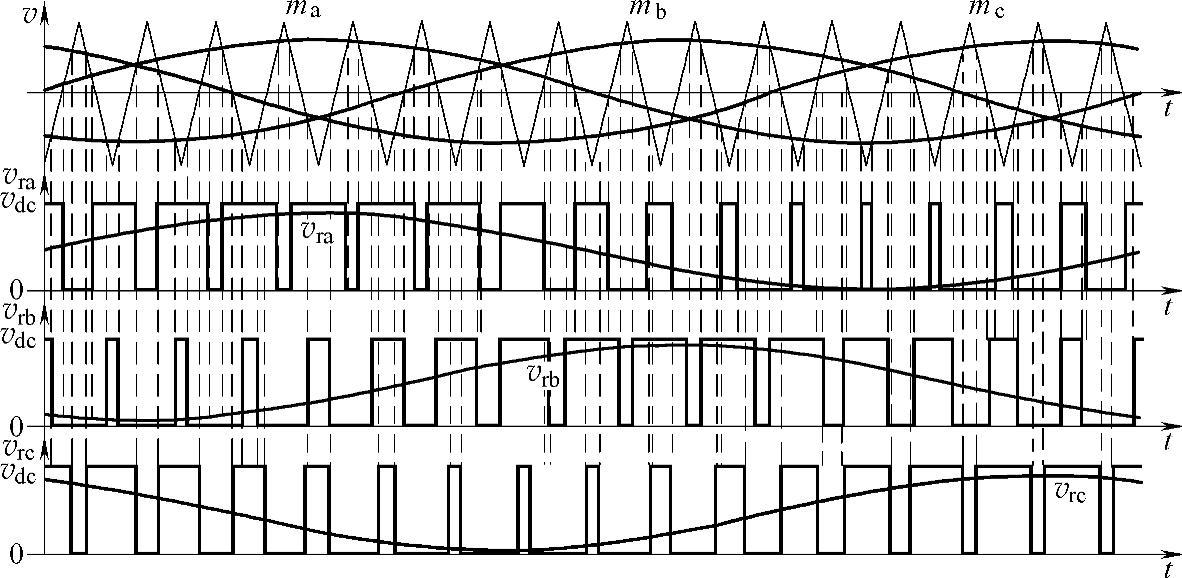
图5-5 三相桥式电路PWM脉宽调制原理

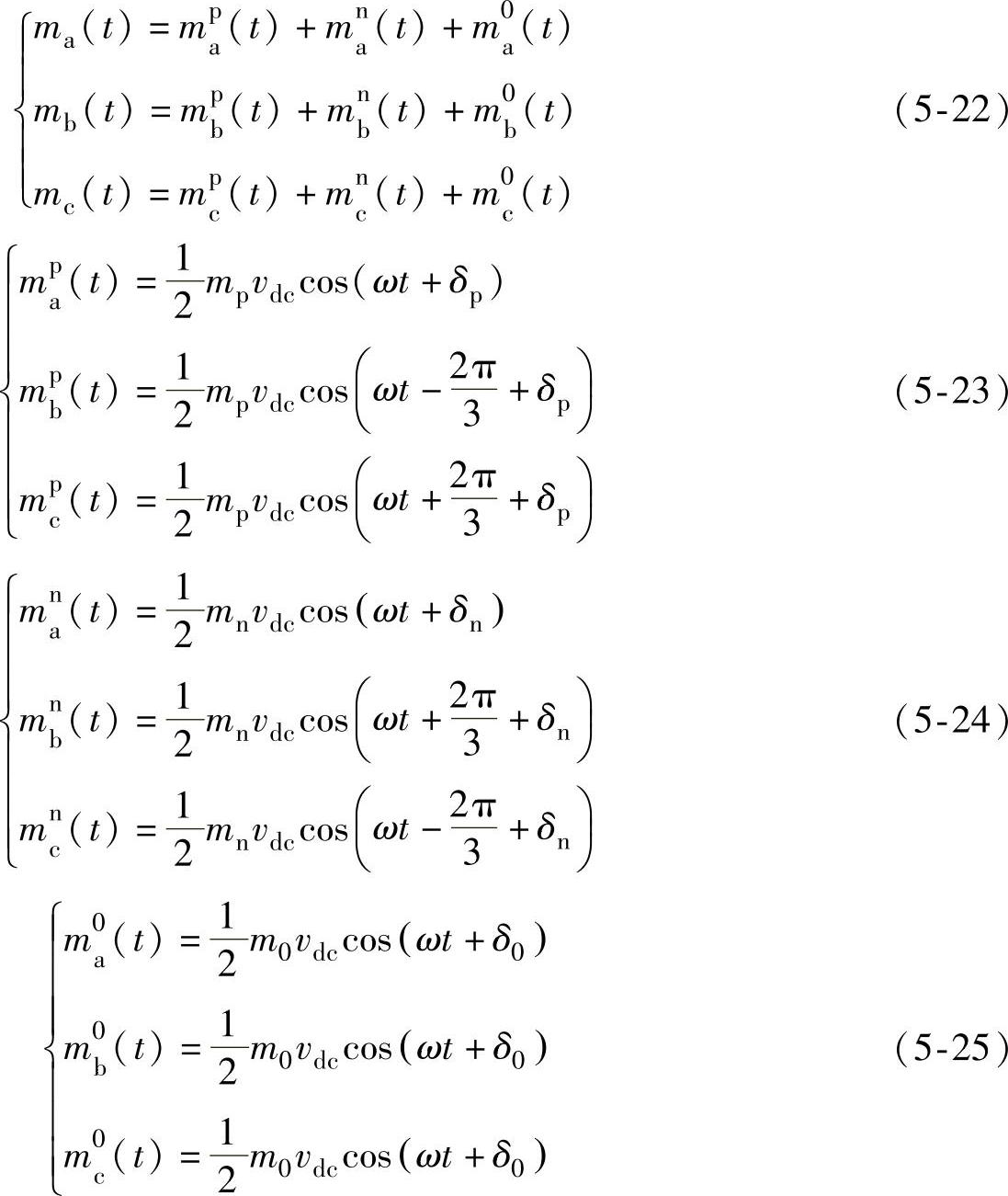
式中，m_p、m_n、m₀为正序、负序和零序调制比，表示整流器开关侧电压调制波峰峰值与直流母线电压比值；δ_p为整流器开关侧电压调制波正序分量滞后于网侧输入电压正序分量的角度；δ_n为整流器开关侧电压调制波负序分量滞后于网侧输入电压负序分量的角度；δ₀为整流器开关侧电压调制波零序分量滞后于网侧输入电压零序分量的角度。根据PWM控制基本原理，可以得到整流器各相开关侧电压相对直流侧参考电位N点的电压表示为

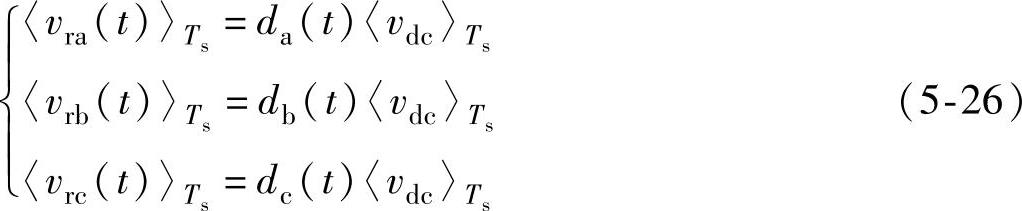
式中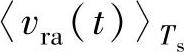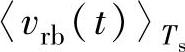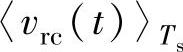，、、为一个开关周期中整流器各相桥臂开关侧相对直流侧参考电位N点的电压平均值，由于整流器直流侧电容很大，认为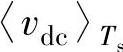在一个开关周期中近似不变，则在一个开关周期中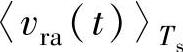、、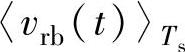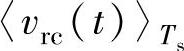与占空比有一一对应关系，结合式（5-23）～式（5-26）可以得到

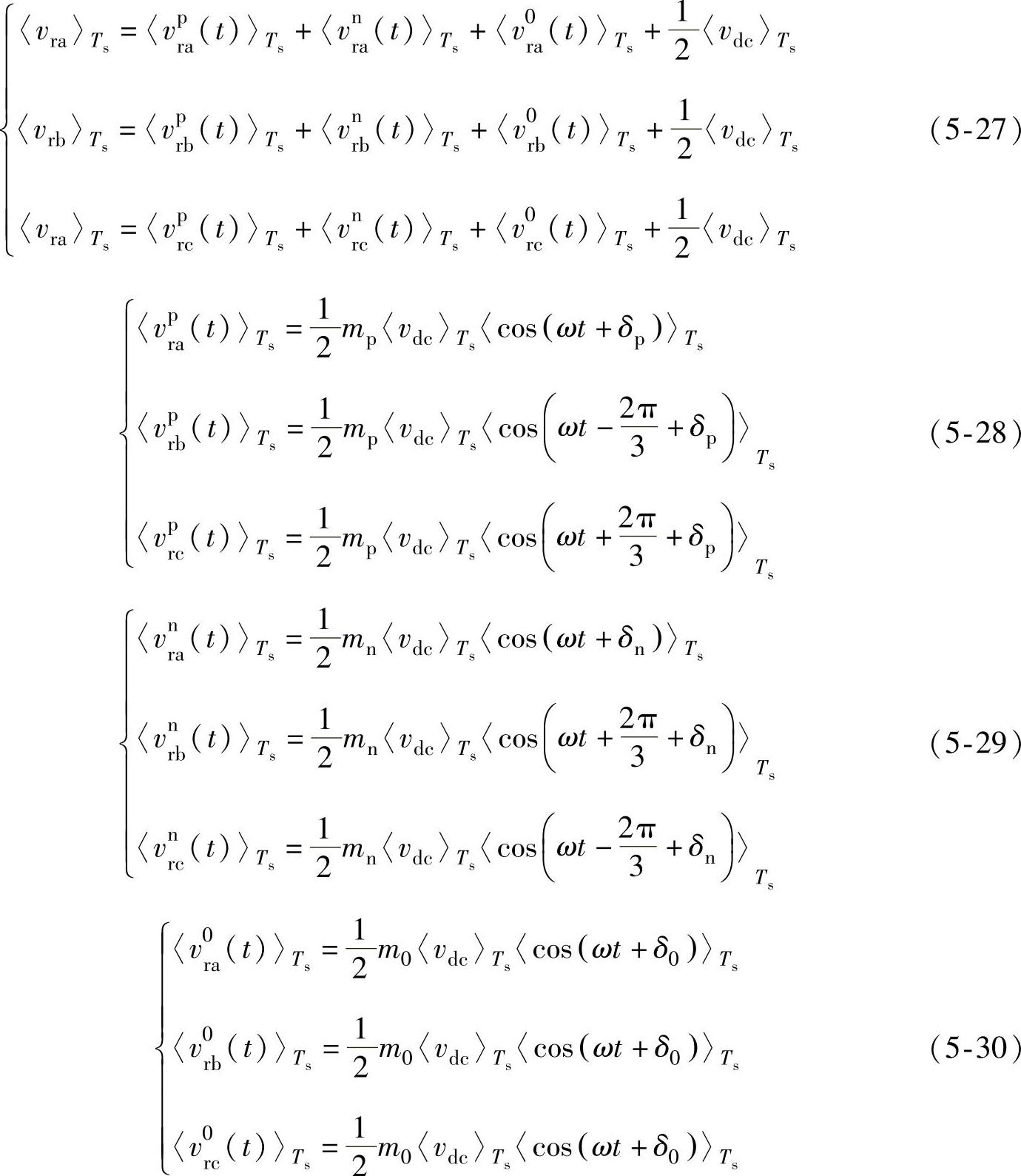
把式（5-28）～式（5-30）代入式（5-18），得到

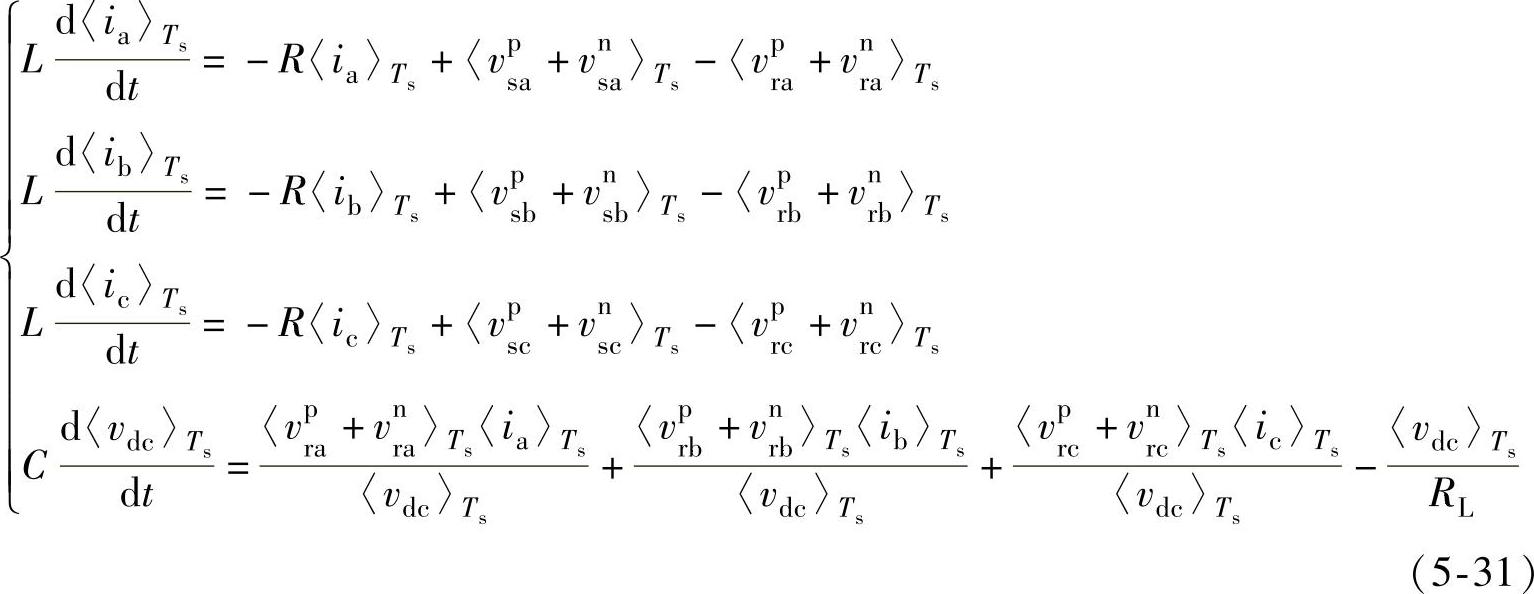
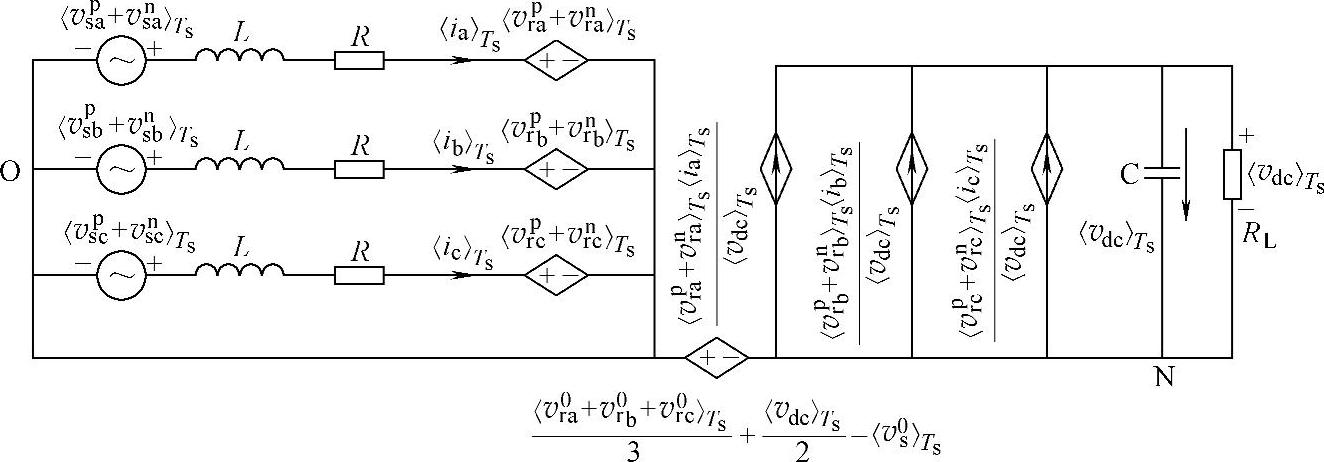
图5-6 三相三线PWM整流器开关周期平均模型的等效电路3

根据式（5-31）可以得到三相三线PWM整流器开关周期平均模型的等效电路，如图5-6所示。图中，整流器PWM的调制波正序和负序电压分量也以电网电压虚拟参考点O为参考点，电网电压虚拟参考点O与整流器直流侧参考电位N电压差v_NO表示为

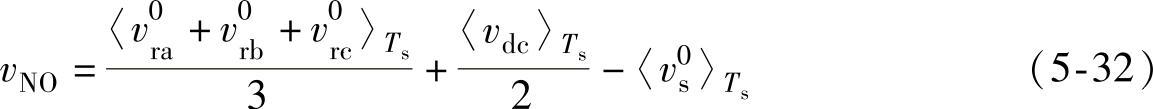
由于式（5-31）表示的基于平均算子的状态空间模型适用于整个工频周期，因此如果只讨论工频情况，可以得到

根据式（5-33）得到的三相三线PWM整流器的工频等效电路如图5-7所示。

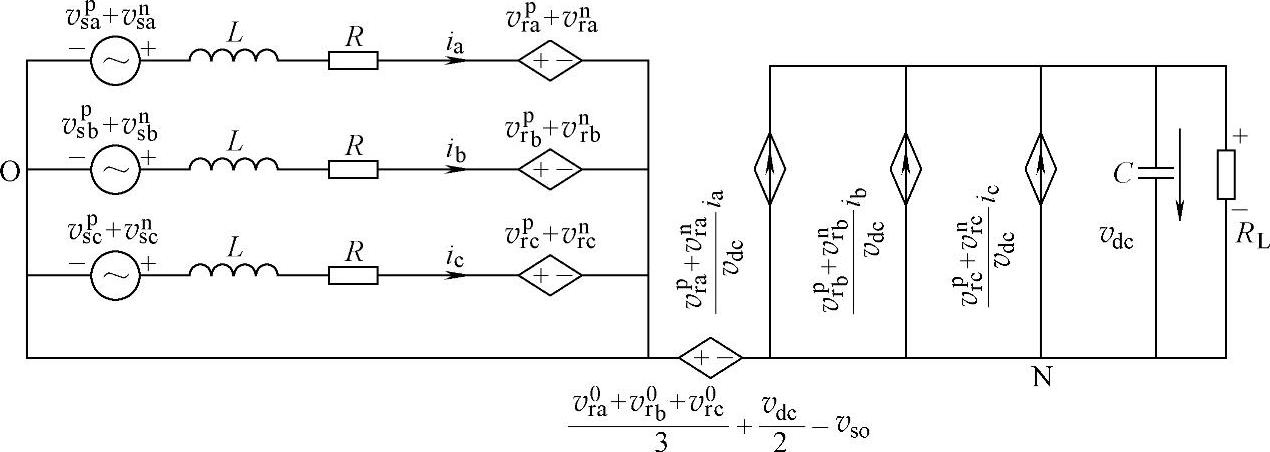
图5-7 三相三线PWM整流器的工频模型

根据式（5-33）和图5-7可以得到，三相三线PWM整流器交流侧已经被分解为三个完全解耦的单相交流电路，电网电压零序分量和整流器调制电压零序分量都不会影响整流器交流电流，只会影响整流器交流侧虚拟参考点和直流电压参考地之间电位差。

为了简化讨论，假设整流器电网电压对称，即电网电压不存在负序分量和零序分量，同时整流器各相无源元件和开关管间参数一致性良好。设定整流器输入电流为

式中，φ是整流器输入电流滞后于网侧输入电压的角度。以整流器a相为例，电压、电流相量关系如图5-8所示。图5-8中横轴为实轴，纵轴为虚轴，A相电网侧输入电压相量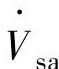、电网侧输入电流相量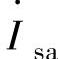和整流器开关侧电压相量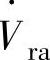的相量关系为

式中，ωL为输入电感感抗，X=ωL；R为电感寄生电阻。

如果忽略PWM整流器滤波电感寄生电阻R，则整流器a相电压、电流的相量

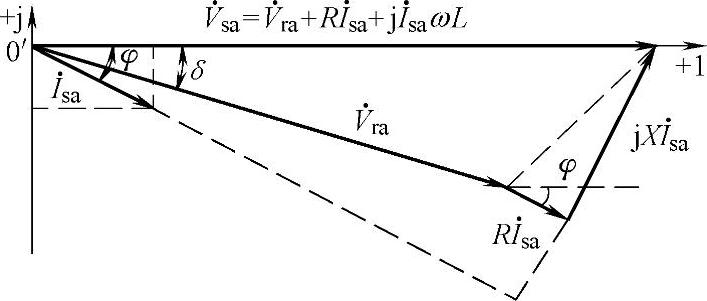
图5-8 考虑电感寄生电阻的电压电流等效相量图

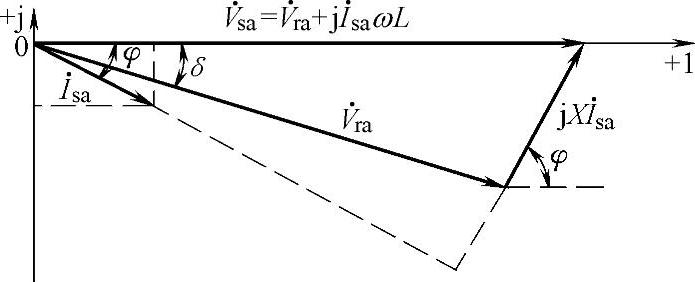
图5-9 忽略电感寄生电阻的电压、电流等效相量图

关系如图5-9所示。a相电网侧输入电压相量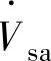、电网侧输入电流相量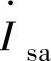和整流器开关侧基波电压相量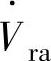的相量关系为

从电网流入整流器a相的复功率的定义是电网电压相量与整流器电感电流共轭相量的乘积，即

在对称系统中，电网流入整流器a相的有功功率和无功功率分别为

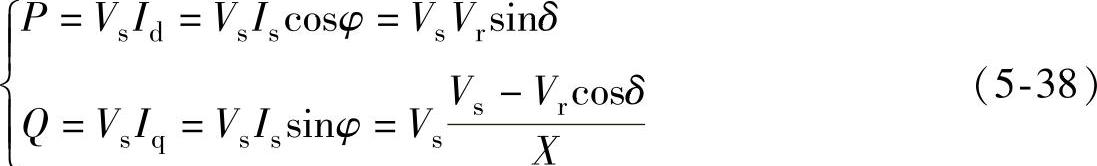
图5-10a所示为电网向整流器注入有功电流和感性无功电流，整流器工作于整流状态，从电网吸收有功功率和感性无功功率，当a相电感电流相量轨迹在A′点时，a相开关管。侧调制电压相量轨迹在A点，此时整流器跟电网只有无功功率交换，不吸收或发出有功功率，电流功率因数为0。

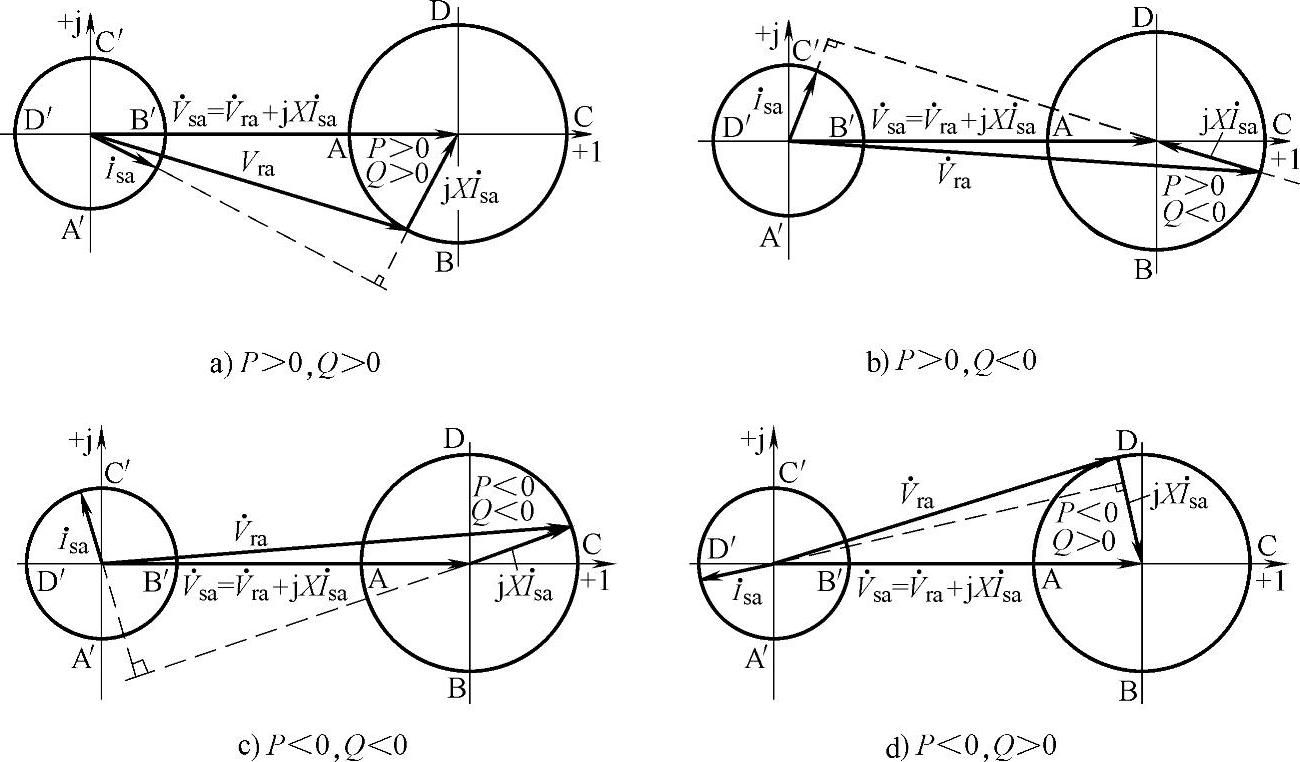
图5-10 忽略电感寄生电阻的电压、电流相量图

图5-10b所示为电网向整流器注入有功电流和容性无功电流，整流器工作于整流状态，从电网吸收有功功率和容性无功功率，当a相电感电流相量轨迹在B′点时，a相开关管侧调制电压相量轨迹在B点，此时整流器跟电网没有无功功率交换，只是单方向从电网吸收有功功率，电流功率因数为1。

图5-10c所示为整流器向电网注入有功电流和容性无功电流，整流器工作于有源逆变状态，向电网发出有功功率和容性无功功率，当a相电感电流相量轨迹在C′点时，a相开关管侧调制电压相量轨迹在C点，此时整流器跟电网只有无功功率交换，不吸收或发出有功功率，电流功率因数为0。

图5-10d所示为整流器向电网注入感性电流，整流器工作于有源逆变状态，向电网发出有功功率和容性无功功率，当a相电感电流相量轨迹在D′点时，a相开关管侧调制电压相量轨迹在D点，此时整流器跟电网没有无功功率交换，只是单方向向电网发出有功功率，电流功率因数为-1。

结合式（5-38），在如图5-10所示的整流器电压、电流相量图中，有功功率总是从相位超前的电源流向相位滞后的电源；滞后的感性无功电流和无功功率总是从幅值高的电源流向幅值低的电源。