Boost型PFC电路工作原理及三相电压波形分析

假设三相单开关Boost型PFC电路工作于电感电流断续模式，而且输入三相电网电压对称，输入三相电网电压可表示为

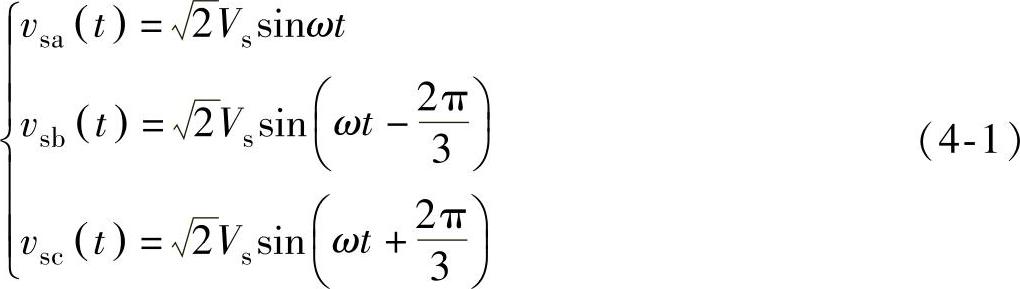
三相电网电压波形如图4-2所示，根据三相电网电压的极性，可以将一个工频周期划分为6个扇区。由于三相单开关Boost型PFC电路的6个扇区中的工作过程类似，下面以扇区Ⅱ为例加以介绍。

在扇区Ⅱ，三相输入电压中a相输入电压v_sa的绝对值最大，a相输入电压的极性为正，b相、c相输入电压的极性均为负。

假定图4-1所示的三相单开关Boost型PFC电路中，开关V采用恒定开关频率控制，占空比为D，电路在扇区Ⅱ中的一个开关周期的工作波形如图4-3所示。由于开关频率f_s远大于电网电压频率f，因此在一个开关周期中可以近似认为三相输入电压v_sa，v_sb，v_sc为恒定。一个开关周期可以划分为四个工作阶段，下面对各阶段进行逐一分析。在下面的阶段分析中，为简化分析，假定电力电子器件均为理想开关器件。

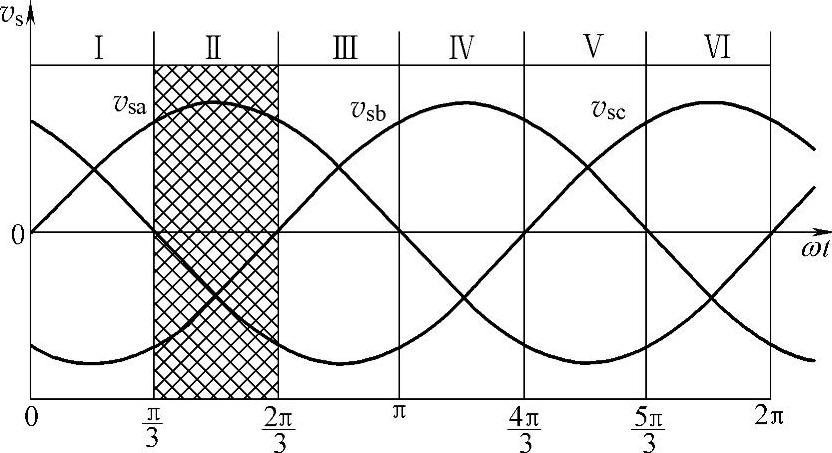
图4-2 三相电网电压波形及扇区划分

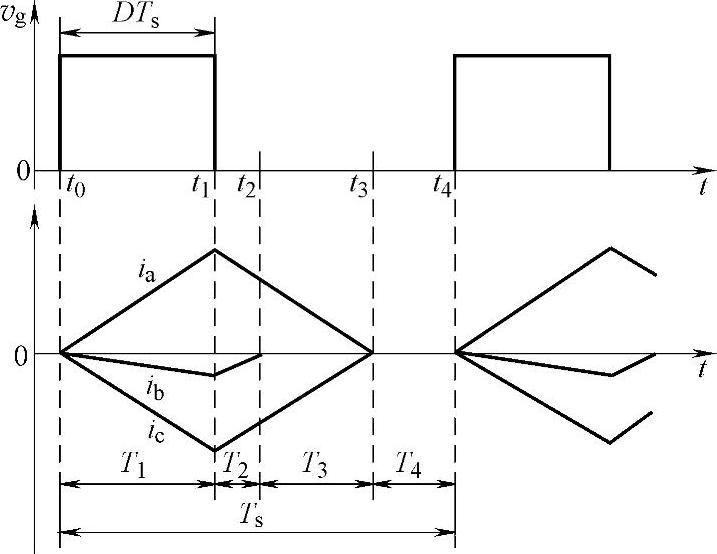
图4-3 三相单开关Boost型PFC电路一个开关周期的工作波形

1.阶段1（t₀＜t＜t₁）：电感储存磁能阶段

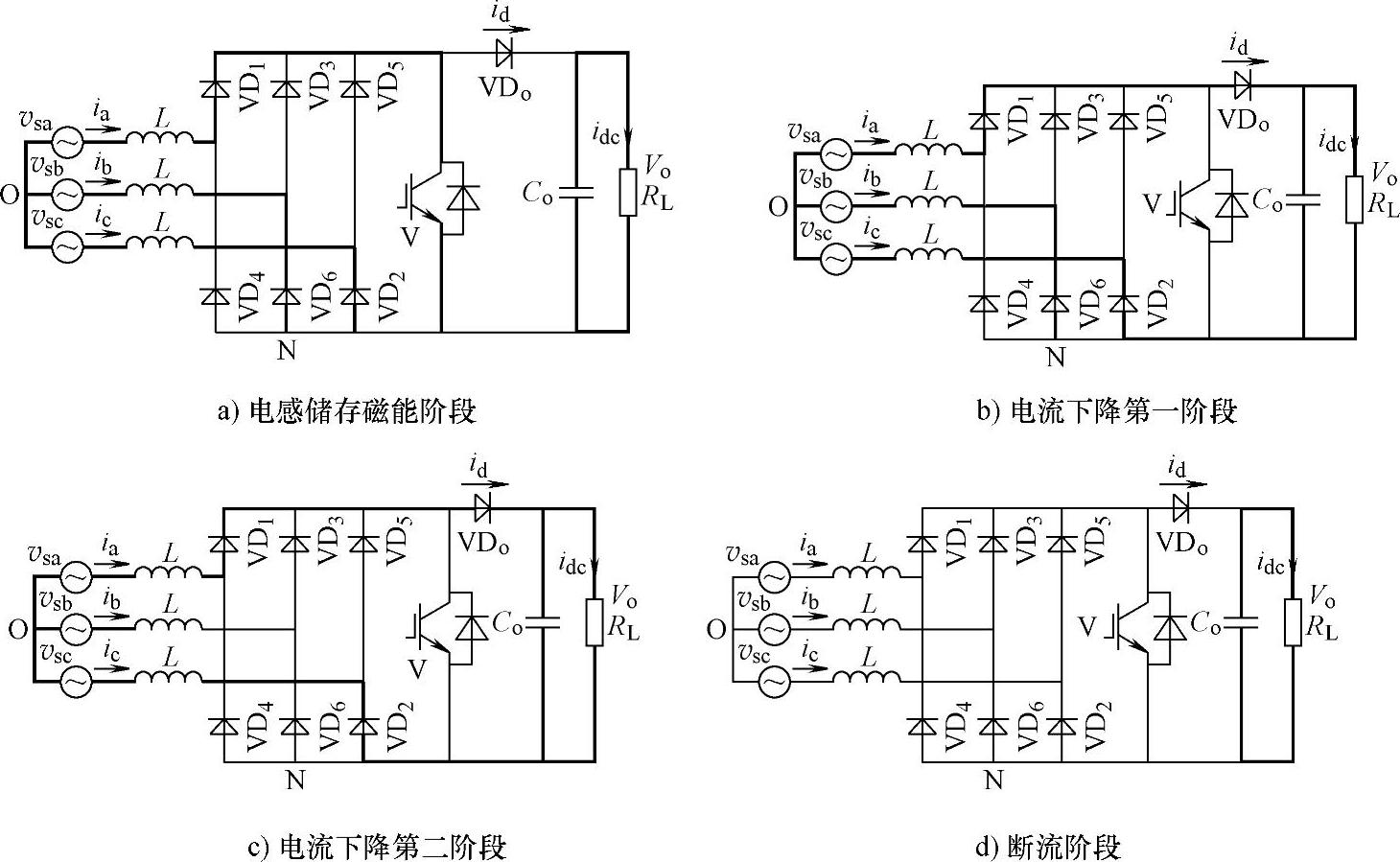
图4-4 DCM下电路各工作阶段等效电路

如图4-3所示，在t₀＜t＜t₁区间内，开关管V的驱动信号v_g＞0，开关管V导通，二极管VD_o承受反压而关断。在该阶段，三相输入电压中，a相输入电压v_sa的绝对值最大，而且v_sa＞0，v_sb＜0，v_sc＜0，可以证明三相整流桥中，VD₁、VD₂和VD₆导通，阶段1的等效电路如图4-4a所示。可见三相输入电压分别连接三个电感，而三个电感的另一端通过开关管V而被连接在一起。本阶段中，三个电感处于储存磁能阶段，而输出部分与输入电源分离，电网中断对负载供电，负载电流由储存在C_o中的能量维持。

由图4-4a可得

式中，v_NO为参考点N与输入电源中点O之间的电压。

将式（4-2）中三式相加，得

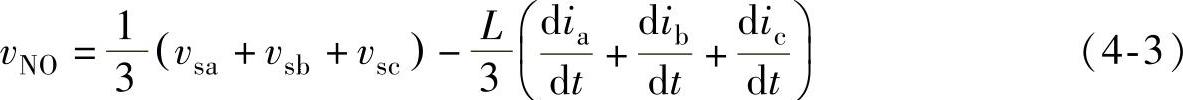
由于三相输入电压对称和输入电流满足基尔荷夫电流定律（KCL），可得

将式（4-4）代入式（4-3），得到

v_NO=0 （4-5）

将式（4-5）代入式（4-2），得到

将式（4-1）代入式（4-6），得到各相电感电流变化率为

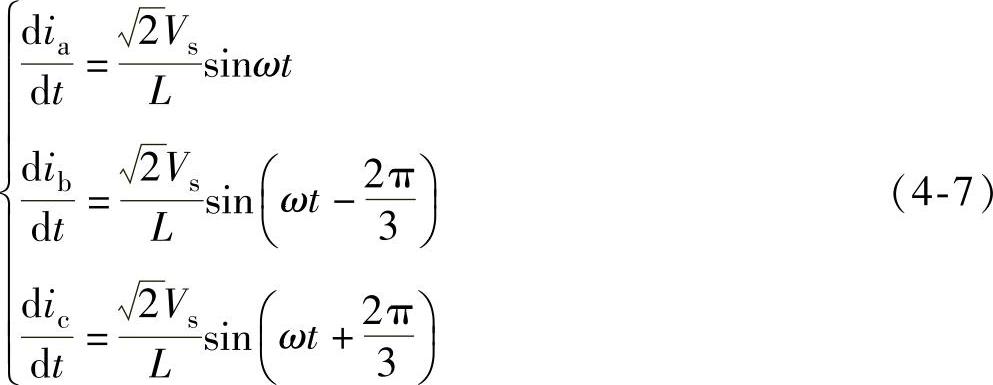
上式表明，阶段1各相电感电流的上升率分别与对应相的电压瞬时值成正比。由于开关周期比工频周期短得多，因此在一个开关周期中，可以认为输入电压恒定。在该阶段，各相电流从零开始线性增加。在阶段1末，即t=t₁=t₀+DT_s，三相电感电流的绝对值分别达到各自的最大值，它们也是每个开关周期中各相电流所能达到的峰值。由式（4-7），可以得到a相电感电流的峰值i_ap为

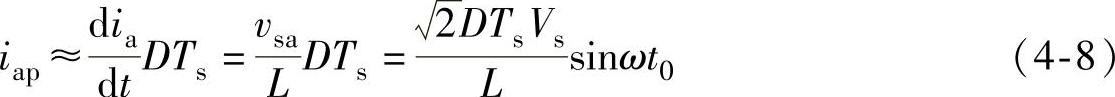
上式表明，在占空比和开关周期一定时，a相电感电流的峰值i_ap与a相电压的瞬时值成正比。对于b相、c相可以得到类似结果，b相电感电流的峰值i_bp为

c相电感电流的峰值i_cp为

2.阶段2（t₁＜t＜t₂）：电感电流下降第一阶段

如图4-3所示，当t=t₁时，开关管V关断，由于电感电流不能突变，三相整流桥中二极管VD₁、VD₂和VD₆保持导通，而且电感电流将通过二极管VD_o续流，阶段2的等效电路如图4-4b所示。在此阶段，三相电感L和输入电源一起向负载输送能量。根据图4-4b的等效电路，可得

将式（4-11）中的前两式相加，得

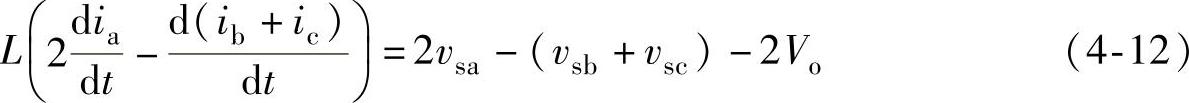
利用式（4-4）化简上式，得到

类似地，可以推得其他两相电感电流在阶段2的变化率，将三相合写如下：

在阶段2，各相电感向输出负载释放磁能，电感电流绝对值下降，下降速率与输出电压和各相电压有关。如图4-2所示，在扇区Ⅱ的前1/2区间中，即π/3，π/2区间，由于c相电压瞬时值的绝对值最小，根据式（4-10），阶段1末，c相电感电流所能达到的峰值最小，即c相电感储能最少，因此在阶段2中，c相电感电流最先下降为零；同理，对于扇区Ⅱ的后1/2区间中，即π/2，2π/3区间，在阶段2中，b相电感电流绝对值最先下降为零。一旦b相电感电流或c相电感电流下降为零，阶段2结束。下面以开关周期处于扇区Ⅱ的π/2，2π/3区间进行分析。

由式（4-14），可以推得在阶段2中b相电流i_b的表达式

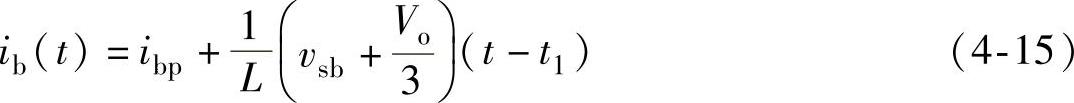
在扇区Ⅱ的后1/2区间中，即[π/2，2π/3]，阶段2的持续时间T₂即为b相电流由其最大值i_bp下降为零所需的时间。由式（4-15），并结合式（4-9）得到阶段2的持续时间T₂为

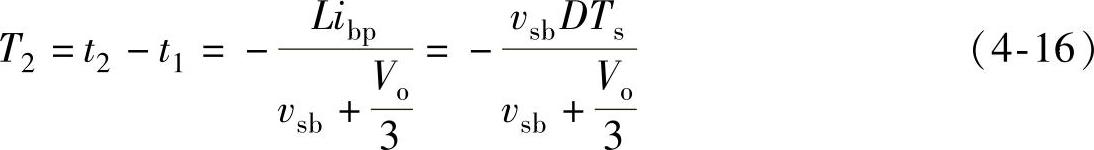
由式（4-14），在阶段2，a相电流i_a可以表示为

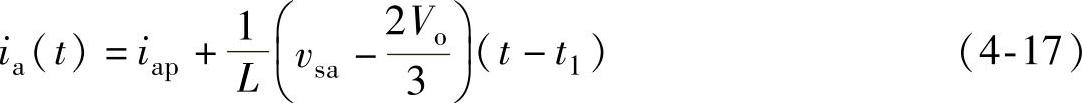(www.xing528.com)

阶段2末的a相电流为

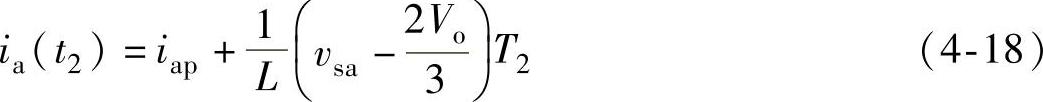
将式（4-8）和式（4-16）代入式（4-18），得到

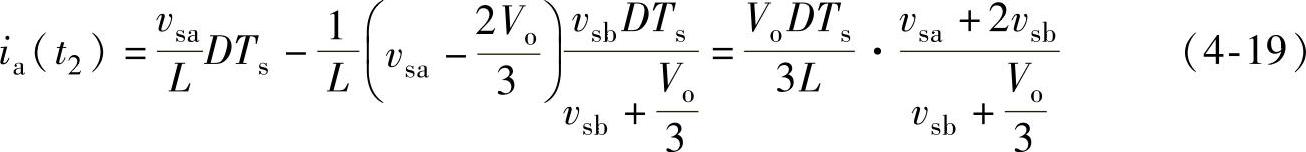
在阶段2，c相电流i_c可以表示为

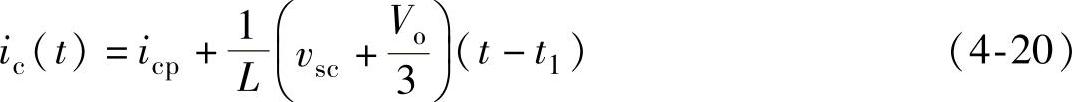
由式（4-4）得到

i_c（t）=-i_a（t）-i_b（t） （4-21）

阶段2末的c相电流为

i_c（t₂）=-i_a（t₂）-i_b（t₂）=-i_a（t₂） （4-22）

3.阶段3（t₂＜t＜t₃）：电感电流下降第二阶段

阶段3的等效电路有两种：如果开关周期处于扇区Ⅱ的前1/2区间中，即π/3，π/2区间，在阶段2中，c相电感电流绝对值最先下降为零；如果开关周期处于扇区Ⅱ的后1/2区间中，即处于π/2，2π/3中，在阶段2中b相电感电流绝对值最先下降为零。现在假定开关周期处于扇区Ⅱ的后1/2区间中，于是在阶段2中b相电感电流绝对值最先下降为零，于是阶段2结束，得到阶段3的等效电路如图4-4c所示。在阶段3中，二极管VD₆关断，而且输入b相电流i_b=0，三相整流桥中只有二极管VD₁和VD₂导通，由图4-4c可以得到

解得

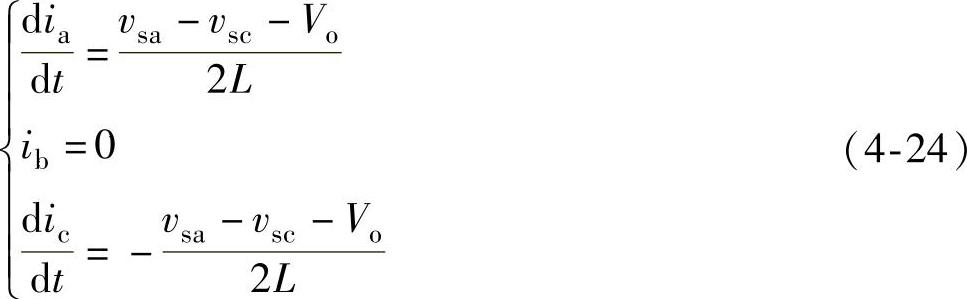
可见，在阶段3中，电感电流下降率与输入电压和输出电压有关。式（4-24）只适用于[π/2，2π/3]区间，对于其他区间也可类似推导。

根据式（4-24），可以得到阶段3的a相电流为

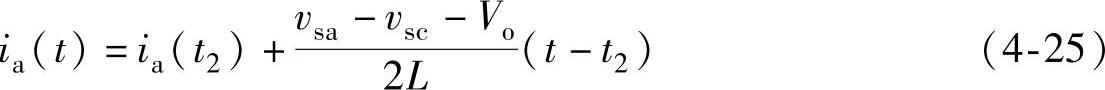
当a相电流下降到零时，阶段3结束。由上式得到阶段3的持续时间为

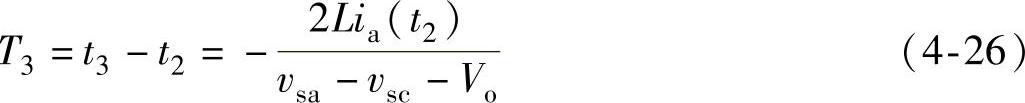
将式（4-19）代入式（4-26），得到

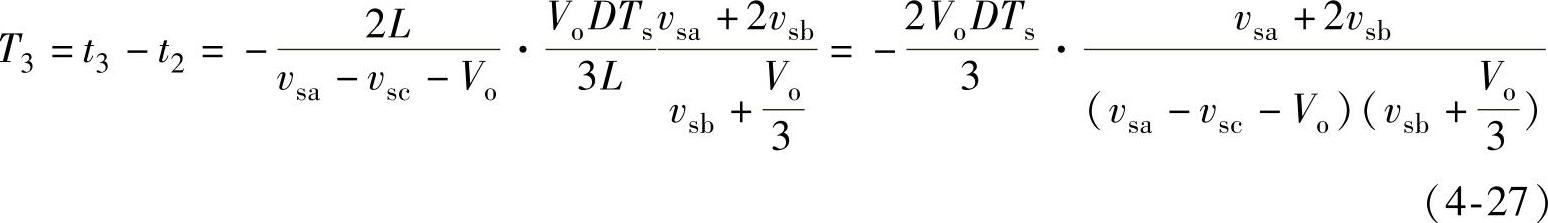
4.阶段4（t₃＜t＜t₄）：断流阶段

在阶段3中，a相和c相电流方向相反但大小相等，同时下降。一旦a相或c相电流下降为零，阶段3即告结束，而后进入阶段4。在阶段4，三相整流桥中所有二极管均截止，开关管V和VD_o也关断，输入三相电感电流都为零，成为断流模式，阶段4的等效电路如图4-4d所示。负载与电源脱离，负载由C_o放电电流维持。

三相单开关PFC电路开关频率远高于电网频率，在一个开关周期内，输入电压瞬时值可近似认为不变。在开关管导通期间，即在阶段1中加在三个Boost电感上的电压分别为各相的相电压，各电感电流线性上升，在这期间，各相的电流峰值正比于对应各相相电压瞬时值。但在开关管关断的阶段2和阶段3中，加在输入各电感上的电压由输出电压与相电压瞬时值共同决定，因而电感上的电流平均值与输入电压瞬时值不再满足线性关系，电流也就产生了畸变。根据以上开关周期的分析，可以得出输入相电流的开关周期平均值的表达式。

以a相为例，当开关周期处于扇区Ⅱ的[π/2，2π/3]区间时，一个开关周期的a相电流如图4-3所示，a相电流的开关周期平均值为

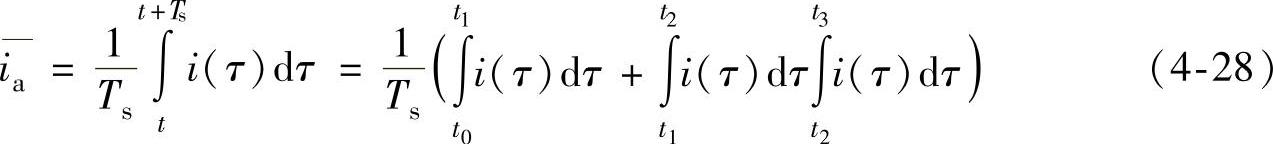
积分用求面积替代，则有

将式（4-8）、式（4-16）、式（4-27）代入式（4-29），化简得到

将式（4-7）代入式（4-30），化简得

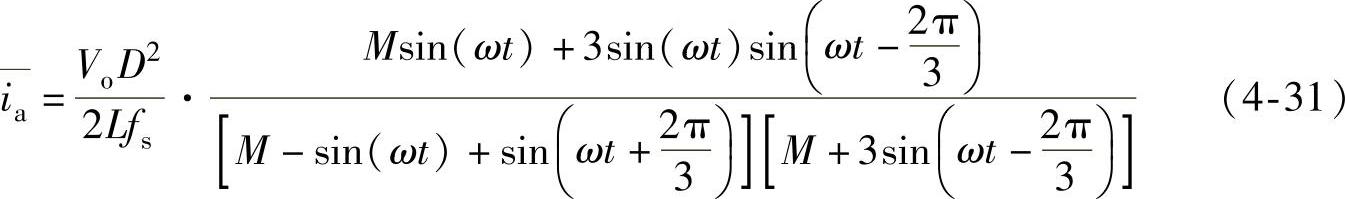
式中，M为输出直流电压和输入交流电压峰值之比，即整流输出电压增益。

同理，可以求得a相电流在其他区间内的表达式，考虑到a相电流为1/4工频周期对称，因此则需写出[0，π/2]区间a相电流的开关周期平均值的表达式。a相电流的开关周期平均值的表达式如下：

定义归一化的输入相电流为

由式（4-33）可见，输入相电流波形与整流输出电压增益有关。图4-5给出归一化的输入相电流波形与整流输出电压增益的关系。从图可知，整流输出电压增益M越大，电流波形正弦度越好。原因是：整流输出电压增益M越大，可以缩短一个开关周期中电流下降模式所占用的时间T₂和T₃，削弱输入电流开关周期平均值对输出电压的非线性依赖关系，从而可以减小电流畸变。图4-6是各次谐波幅值与整流输出电压增益M的关系。

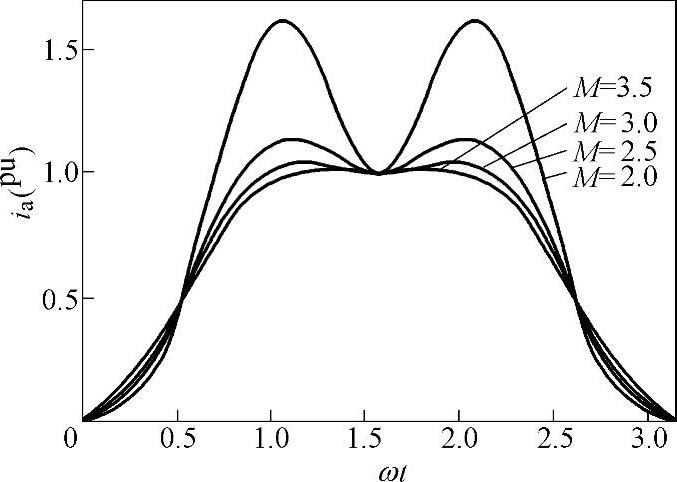
图4-5 电流波形与整流输出电压增益M关系

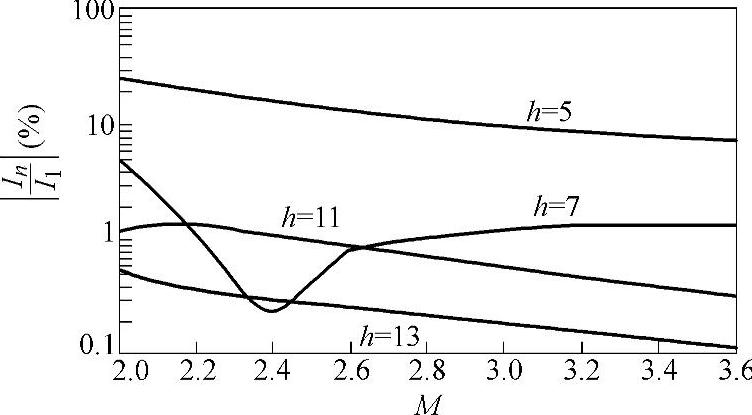
图4-6 各次谐波幅值与整流输出电压增益M的关系

从上面的分析可知，为了减小网侧输入电流的畸变，需要提高输出电压，但提高输出电压将增大电路中开关管的电压应力，同时使得后级的电力电子变换器的输入电压升高。

三相单开关Boost型PFC电路的优点是：仅使用一只开关管，电路和控制简单；由于电路工作在DCM下，Boost二极管VD_o不存在反向恢复问题，且开关管在零电流下开通，开通损耗较小。但是，三相单开关Boost型PFC电路工作在DCM时存在输入电流THD较大的问题，需要有较大的电源侧EMI滤波器。三相单开关Boost型PFC电路一般应用于输出功率小于10kW场合，并且对输入电流THD要求不高的场合。