图3-23所示为单相Boost型PFC变换器工作在CRM时电感电流波形,由于采用VF控制,因此开关频率是变化的。为简化设计,VF控制采用恒定开通时间控制策略。下面分析开关频率与电路参数之间的关系。
在CRM中,一个开关周期由两个阶段构成。在每个开关周期之初,电感电流总是从零开始上升,达到要求的峰值后,就开始下降,直到电感电流为零。一旦电感电流为零,立即启动下一个开关周期。因此在CRM中,电感电流的波形由一系列的三角波组成。
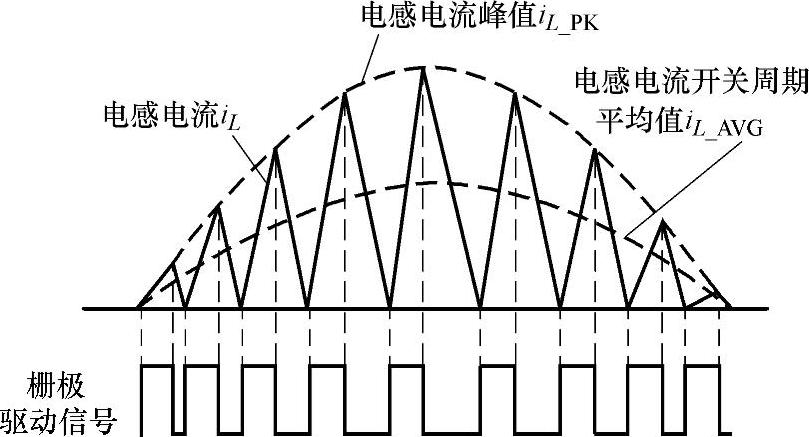
图3-23 在CRM中电感电流波形
在CRM中,一个开关周期由两个阶段构成,对应的等效电路如图3-24所示。为简化分析,在以下分析中,假定开关管为理想开关器件,开关管导通时,其压降为零,开关管关断时,其电阻为无穷大。
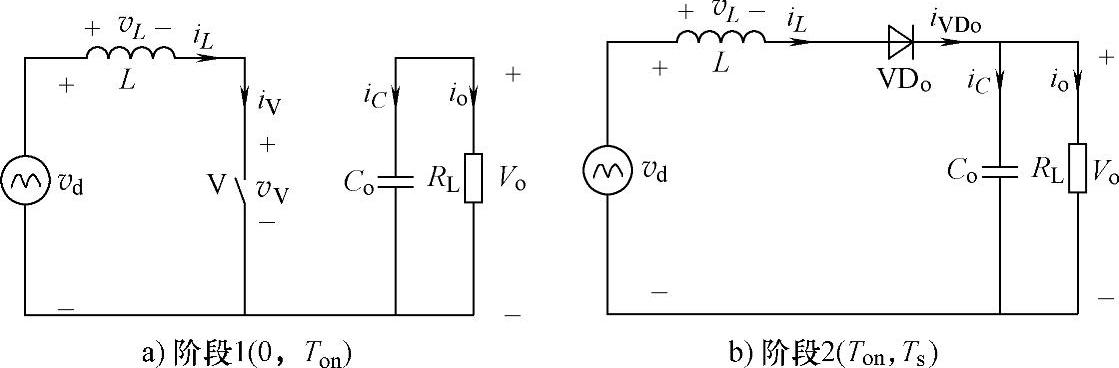
图3-24 CRM下工作时等效电路
在阶段1(0,Ton)中,开关管V导通,而VD0处于关断状态,阶段1的等效电路如图3-24a所示。电压vd(ωt)加在电感L上,电感上电压vL可表示为

电感电流变化率diL/dt为

由于开关周期Ts相对于工频周期非常的短,因此近视认为在一个开关周期中电网电压保持恒定,由式(3-47)得到
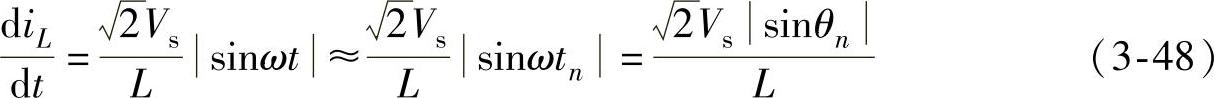
式中,θn为在一个工频周期中,第n个开关周期的开始时刻,θn=ωtn。
由式(3-48),可以解出电感电流
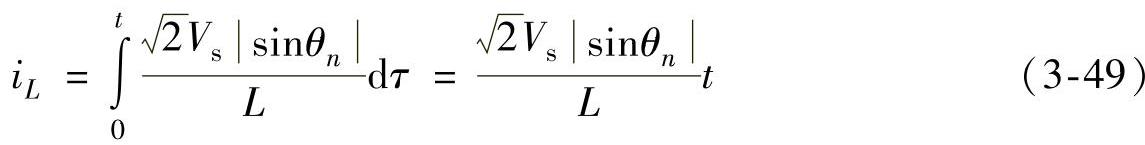
上式表明:在阶段1中,电感电流iL从零开始线性上升。在阶段1末,即t=Ton,电感电流达到峰值为
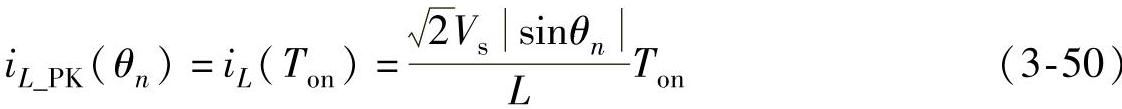
在每个开关周期中,电感电流峰值iL_PK(θn)是sinθn的函数。如果VF控制采用恒定开通时间控制策略,即导通时间Ton为恒定值,那么在半个工频周期中,电感电流的峰值的包络线按照正弦变化,如图3-23所示。
由于在阶段1,二极管VDo处于关断状态,电流iVDo=0,因此输出负载电流只能依靠C的放电来维持,io=-iC。
在阶段2(Ton,Ts)中,开关管V关断,而VDo处于导通状态,阶段2的等效电路如图3-24b所示。电压vd(ωt)-Vo加在输入电感L上,于是电感上电压vL可表示为
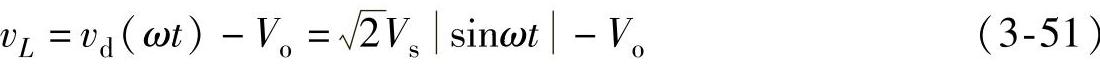
电感电流的变化率为
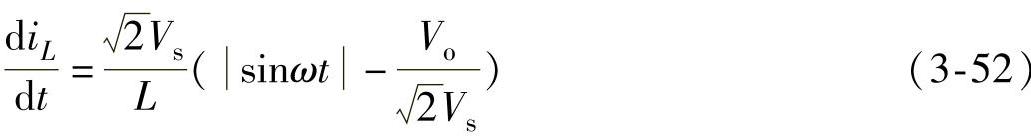
假定开关周期Ts相对工频周期非常的短,这样可以近视认为在一个开关周期中,电网电压保持恒定,于是式(3-52)可近似为
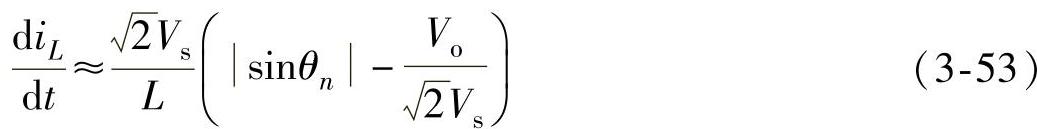
由于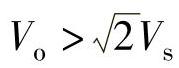 ,因此上式的右边为负,表明在阶段2中,电感电流下降,即表示电感L处于释放磁能状态。在阶段2中,电感L与输入电源一起向输出负载输送电能,并对电容C充电,电容C中储存的电能将增加。
,因此上式的右边为负,表明在阶段2中,电感电流下降,即表示电感L处于释放磁能状态。在阶段2中,电感L与输入电源一起向输出负载输送电能,并对电容C充电,电容C中储存的电能将增加。
由式(3-53),得到在阶段2中的电感电流
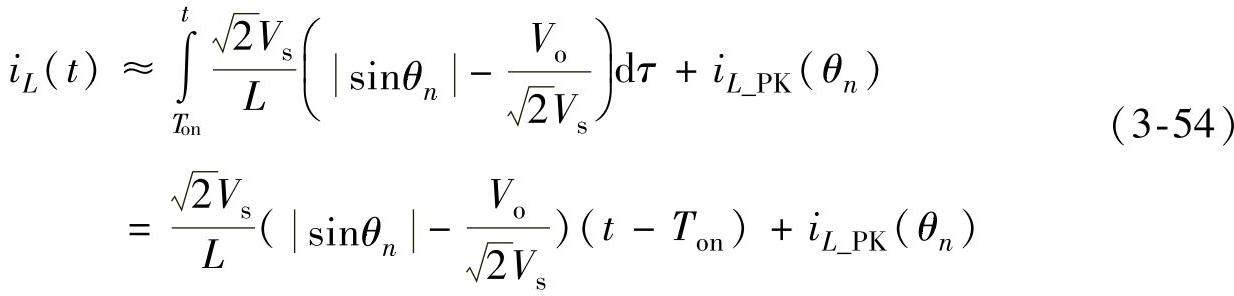
一旦电感电流下降到零,阶段2就结束,于是开始下一个开关周期。令上式在t=Ts时为零,以便求解开关周期Ts,即
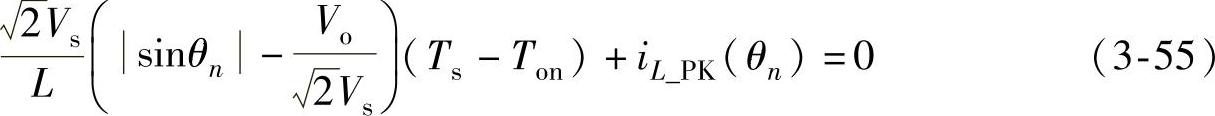
阶段2的持续时间Toff为
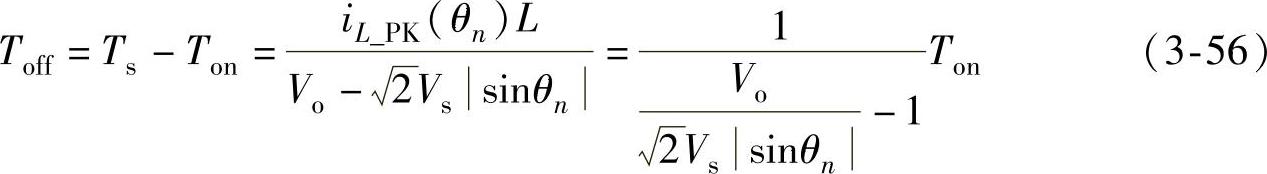
阶段2的持续时间Toff与输出电压Vo、输入电压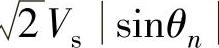 、开关导通时间Ton有关。
、开关导通时间Ton有关。
在CRM中,电感L在阶段1储存磁能将在阶段2未全部向输出释放,即在阶段2末的电感电流的值等于零。
开关周期为Ts=Ton+Toff,利用式(3-56),得到恒定导通时间控制时开关周期

开关频率为
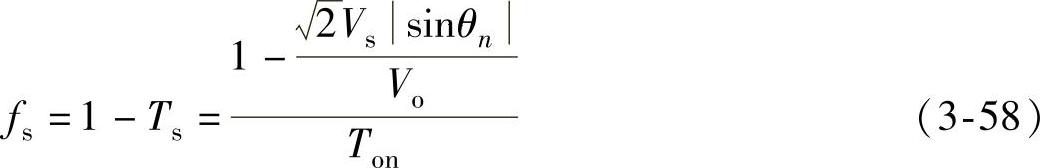 (https://www.xing528.com)
(https://www.xing528.com)
上式表明,单相Boost型PFC变换器工作在CRM时,在一个工频周期中,开关频率fs是变化的,如图3-25所示。当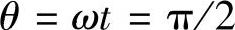 时,开关频率fs达到最低值,即
时,开关频率fs达到最低值,即

定义归一化开关频率fs*为
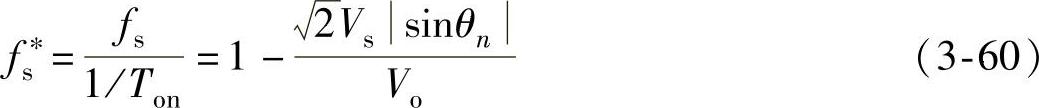
占空比为
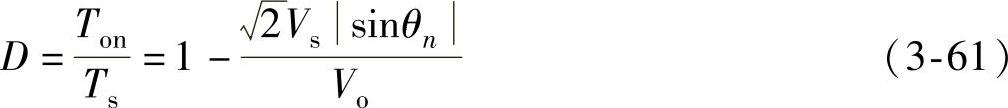
上式与CCM时的占空比式(3-31)相同。
图3-25给出了开关频率随着输入交流电网电压正弦波形变化的情况。图3-25a中输入交流电压的有效值Vs=230V,输出直流电压Vo=400V,可见在输入交流电压的峰值时开关频率约为输入交流电压过零时刻的开关频率的五分之一。图3-25b中,输入交流电压的有效值Vs=90V,输出直流电压Vo=400V,可见在输入交流电压的峰值时,开关频率约为输入交流电压过零时刻的开关频率的三分之二。可见,输入电压的有效值愈小,开关频率fs的变化范围愈窄。
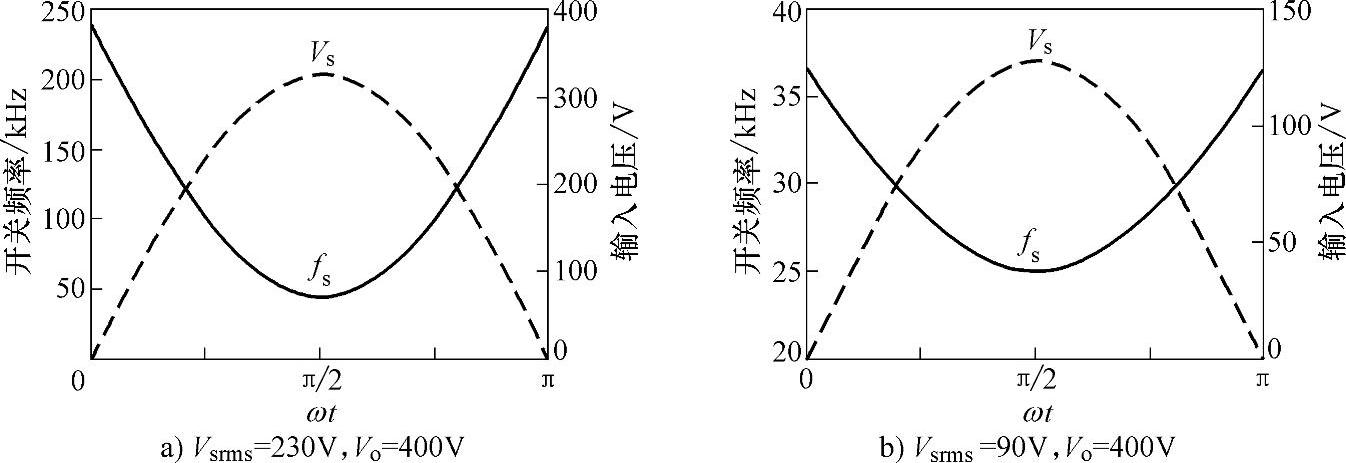
图3-25 在CRM下开关频率与输入交流瞬时值的关系
PFC变换器的输入交流电流的有效值Is是直流输出功率Po、变换器效率η和输入电压有效值Vs的函数。假定输入功率因数为1,输入交流电流的有效值Is为

如图3-23所示,一个开关周期的电感电流呈三角形,电感电流峰值的包络线iL_PK是电感电流开关周期平均值iL_ avg的两倍,即
iL_PK(θ)=2iL_ avg(θ) (3-63)
在半个工频周期中,电感电流的开关周期平均值iL_ avg可以近似为正弦波,其有效值为IL_ avg=Is,即iL_ avg可表示为

将式(3-64)代入式(3-63),得到iL_PK为

在电感电流达到峰值的时刻,iL_PK(θn)=ILmax(θn)。在θ=θn时,由式(3-65)得到

重写式(3-50)为
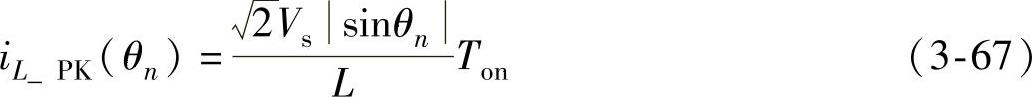
结合式(3-66)和式(3-67),得到

将式(3-62)代入式(3-68),得到

将式(3-69)代入式(3-58),得到
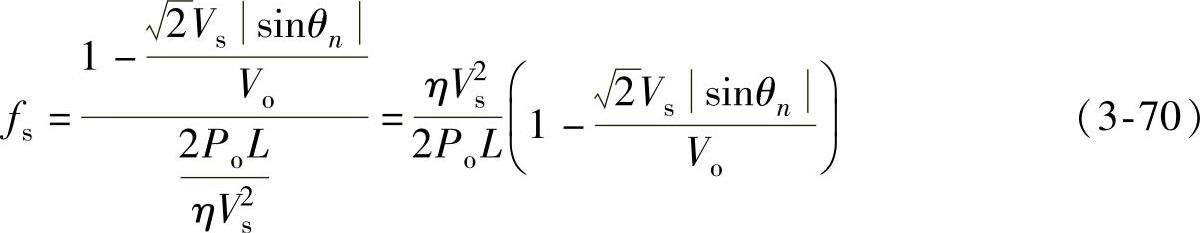
当θn=π/2时,开关频率达到在半个工频周期中的极小值fs_min为

假定输出电压Vo、输出功率Po、变换器效率η和电感L一定,开关频率的极小值fs_min与输入电压有效值Vs有关。假定输出电压Vo=400V,输入电压有效值Vs的变化范围为90~265V,图3-26给出了开关频率极小值fs_min与输入电压有效值Vs关系曲线,这里以输入Vs=90Vrms时开关频率极小值fs_min为规一化基准。
可见,当输入电压有效值Vs最大时,fs_min为最小,有
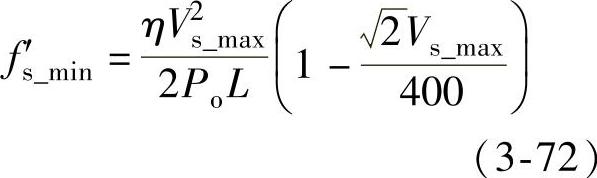
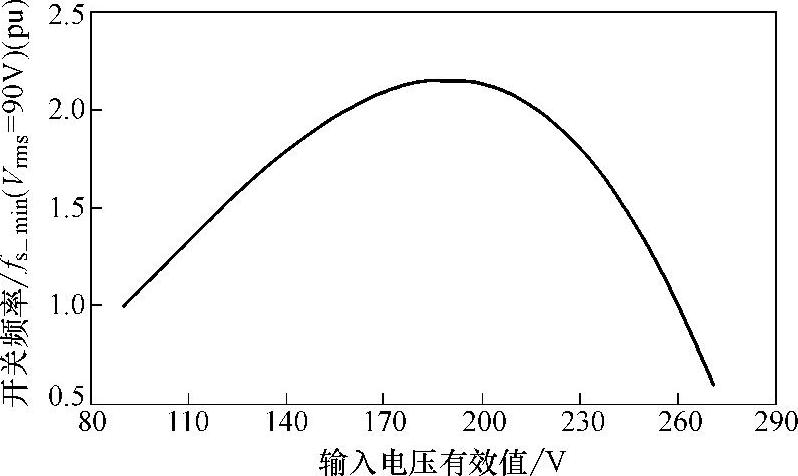
图3-26 开关频率极小值fs_min与输入电压有效值Vs关系曲线
上式可以用于Boost型电感值的设计,假定最小开关频率已经确定,这样可以由下式确定Boost型电感值为
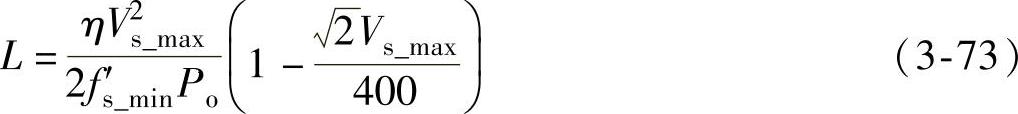
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




