电路原理分析详解

将Boost型变换器作为子电路插入图3-3得到单相Boost型PFC电路，如图3-10a所示。由图可见，在单相桥式整流电路和负载电阻R_L之间插入由点画线框所包含的Boost型变换器，Boost型变换器由开关管V和二极管VD_o以及输入电感L和输出电容C_o组成。

1.开关周期阶段分析

假定通过电感L的电流i_L在一个工频周期中保持连续，也即不存在电感电流持续为零的区间，就称该电路工作在CCM。如果输出滤波电容C_o足够大，那么输出电压可以近似视为恒定值v_o=V_o。设电网电压v_s（ωt）为

式中，ω为电网工作角频率，ω=2πf，f为电网频率。如果忽略输入整流桥二极管的导通压降，整流桥的直流侧输出电压v_d的瞬时值为

设Boost型变换器中的开关管V采用恒定开关频率、变占空比D控制。设开关频率为f_s，开关周期T_s=1/f_s。为简化分析，在以下分析中，认为开关管为理想开关器件，即开关管导通时其压降为零，开关管关断时其电阻为无穷大。在CCM下，一个开关周期T_s可以分为两个阶段。

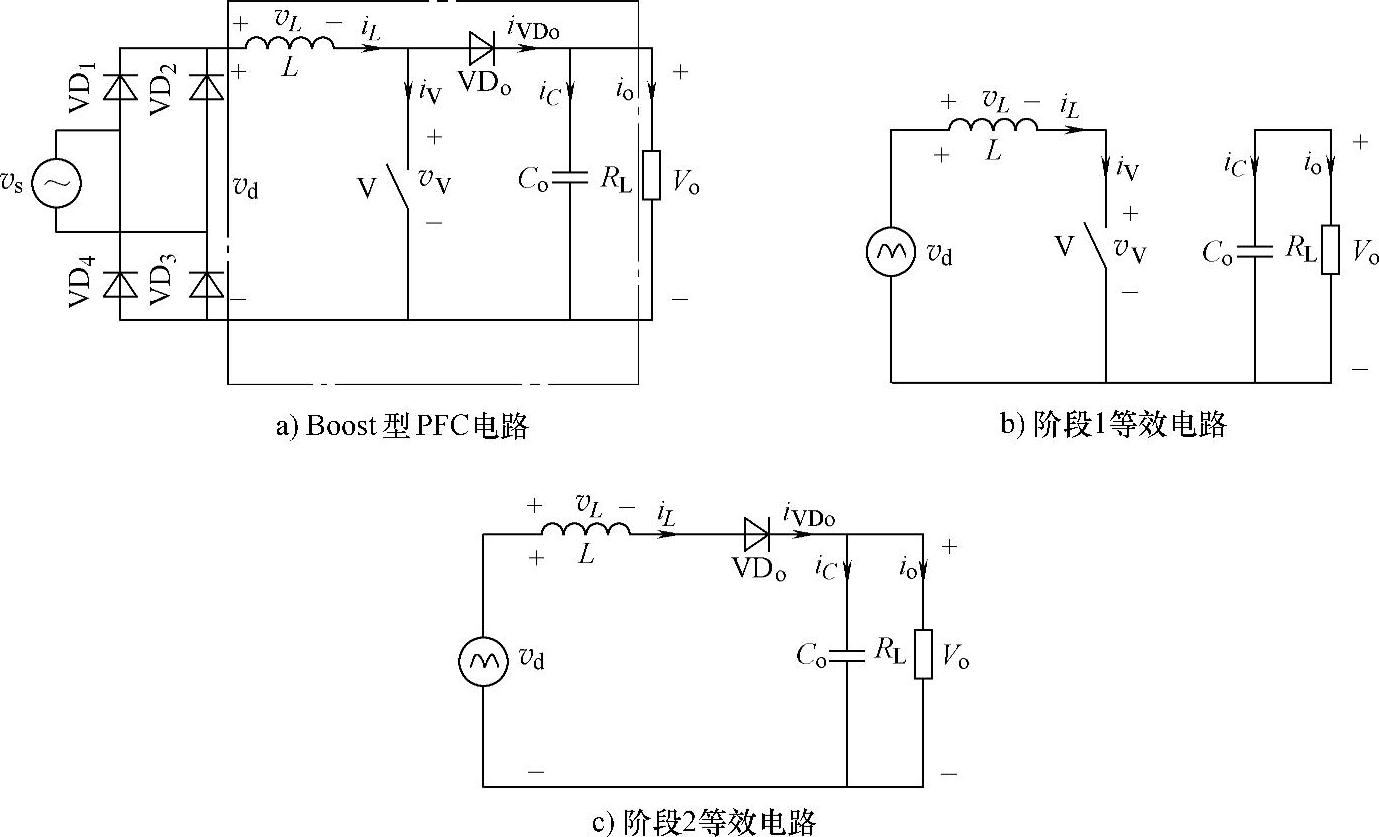
图3-10 CCM Boost型PFC电路与阶段分析等效电路

（1）阶段1（0，DT_s）：Boost型电感储存磁能阶段

阶段1的等效电路如图3-10b所示，开关管V处于导通状态，而二极管VD_o处于关断状态，Boost型电感处于储存磁能阶段。电压v_d（ωt）加在电感L上，电感上电压v_L为

根据法拉第电磁感应定律，电感上电压v_L可以表示为

结合式（3-22）和式（3-23），得到电感电流变化率

上式表明，在阶段1，电感电流处于上升状态，其上升率按正弦规律变化。

由于在阶段1，二极管VD_o处于断态，电流i_VDo=0，输出负载电流只能依靠C_o放电维持，i_o=-i_C。

（2）阶段2（DT_s，T_s）：Boost型电感释放磁能阶段

阶段2的等效电路如图3-10c所示。开关管V处于关断状态，而VD_o处于导通状态，Boost型电感处于释放磁能阶段。电压v_d（ωt）-V_o加在输入电感L上，电感电压v_L为

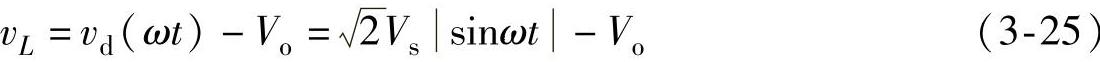
在阶段2中，电感L的电流变化率为

由于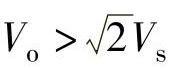，推导得

上式表明，在阶段2中，电感电流下降，即表示电感L处于释放磁能状态。在阶段2，电感L与输入电源一起，向输出负载输送电能，并对电容C_o充电。在此期间，滤波电容C_o中储存的电量将增加。电感L在阶段1储存磁能，将一部分磁能在阶段2向输出释放，但由于在CCM下，电感L储存了足够的磁能，因此在阶段2末，电感L中的磁能尚未耗尽，即在阶段2末的电感电流的值大于零。

式（3-24）和式（3-26）表明，电感电流的变化率随相位角θ=ωt而变化。当θ=0时，输入电网电压瞬时过零，阶段1的电感电流上升率等于零；而阶段2的电感电流下降率di_L/dt=-V_o/L，很高。当θ=π/2时，在输入电网电压瞬时达到峰值，阶段1的电感电流上升率di_L/dt=2V_s/L，很高；下降率为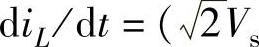-V_o）/L，却较低。

2.占空比D

在CCM下，一个开关周期中电感上的电压v_L可表示为

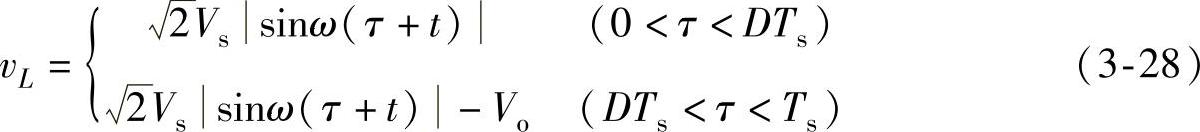
假定开关周期T_s比工频周期T要小得多，在一个小时间段内近似认为电路处于稳态，于是可粗略认为在一个开关周期中电感上能量达到平衡状态，这样，电感电压v_L在一个开关周期中的平均值为零，即

将式（3-28）代入式（3-29）左边，可以得到

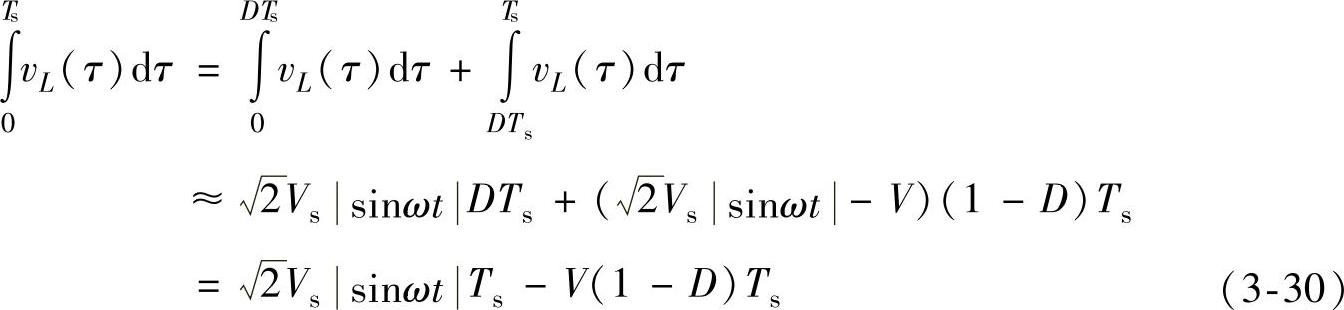(www.xing528.com)

结合式（3-29）和式（3-30），解得

图3-11所示为占空比函数D（t）和PWM信号。在CCM下，在半个工频周期中，开关管V的占空比随电网输入电压按正弦波规律变化。当输入电压的瞬时值过零时，占空比达到最大值1；而当输入电压的瞬时值达到峰值时，占空比达到最小值。因此，为了实现功率因数校正，需要有按照图3-11所示的占空比函数D（t）规律，对开关管V通断进行PWM控制。

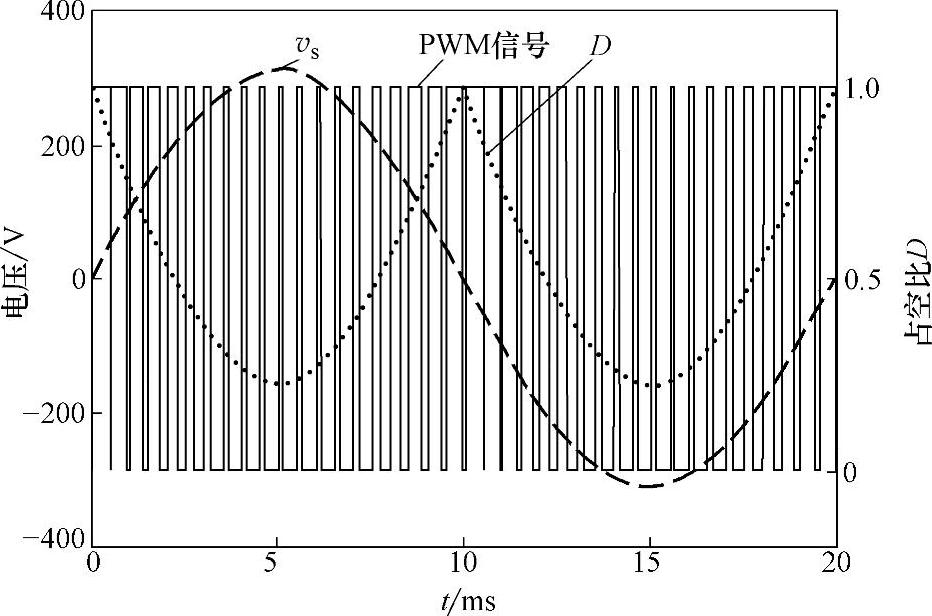
图3-11 占空比函数D（t）和PWM信号

式（3-31）仅是CCM的必要条件，但仅按照式（3-31），控制占空比D，一般并不能实现输入电网电流的正弦化目标，通常采用电流瞬时值控制，使得输入电网电流瞬时值跟踪电网输入电压正弦波的变化，达到单位功率因数和输入电流正弦化的目标。

3.输出滤波电容电流纹波

如果频率调制比m_f=f_s/f和电感L值足够大，i_L谐波分量很小，i_L电流可以近似表示为

这样电网输入电流为

在一个开关周期中，通过开关管V的电流可表示为

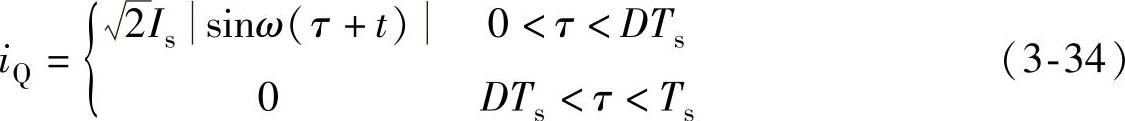
类似地，通过Boost二极管VD_o的电流i_VDo可表示为

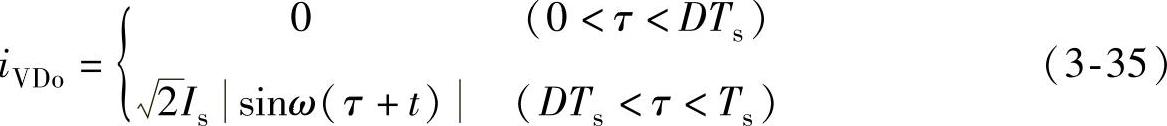
假定输出端滤波电容C_o值足够大，二极管VD的电流i_VDo中交流分量几乎全部流入输出滤波电容C_o。这样，流入电容的电流i_C可近似为

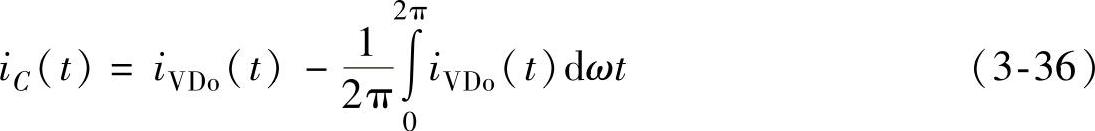
电容电流i_C波形如图3-12a所示。对电容电流i_C作傅里叶分析，得到电容电流i_C的谐波频谱如图3-12b所示。在低频段，存在两倍于电源频率的分量；在高频段，存在以开关频率f_s或开关频率倍数为中心的谐波分量及其边频带，其中以开关频率f_s为中心的谐波分量及其边频带为最显著。交流分量将主要流入输出滤波电容，不仅造成输出电压的脉动，同时会在滤波电容的寄生等效串联电阻（ESR）上产生功率损耗。在选择输出滤波电容器C_o时，需要综合考虑两倍工频的电流分量和开关频率f_s引起的高频电流分量。

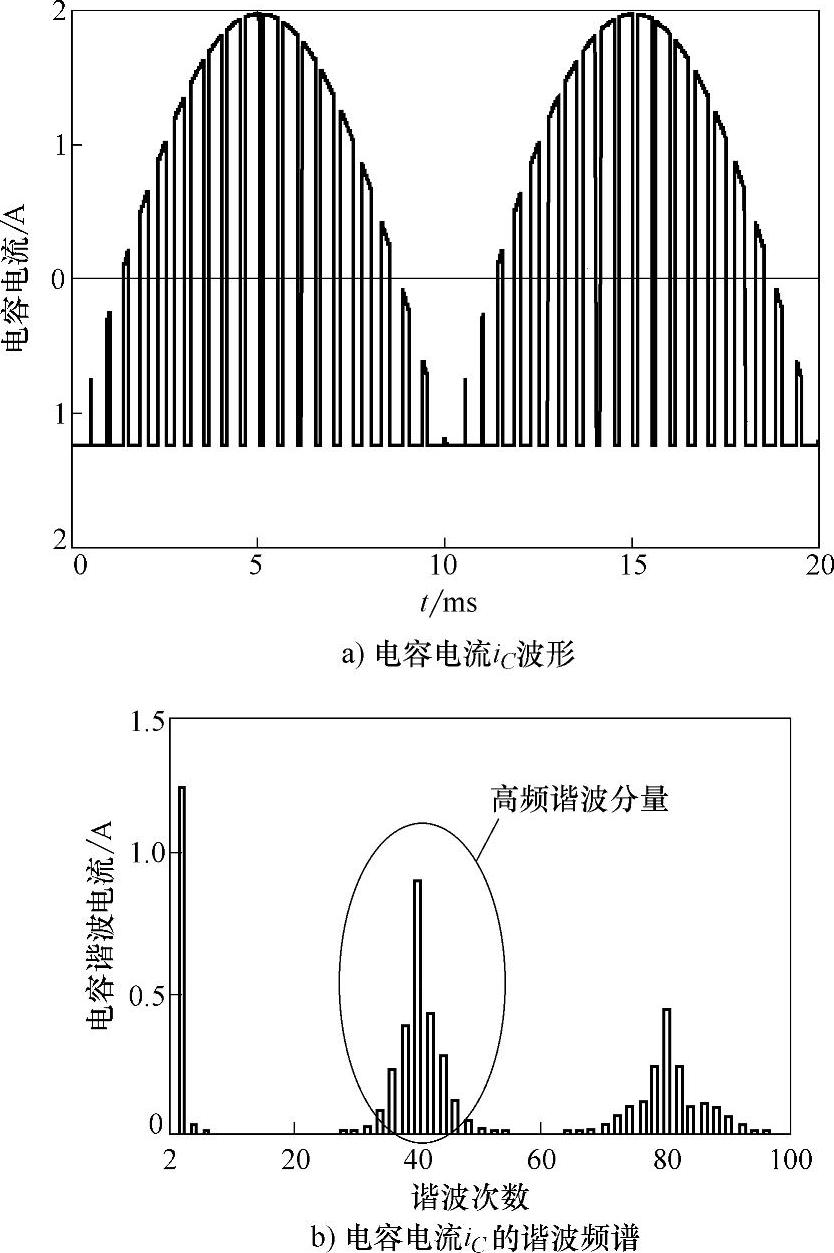
图3-12 电容电流i_C波形及谐波频谱

忽略开关频率高频分量，通过二极管VD的电流的低频部分为

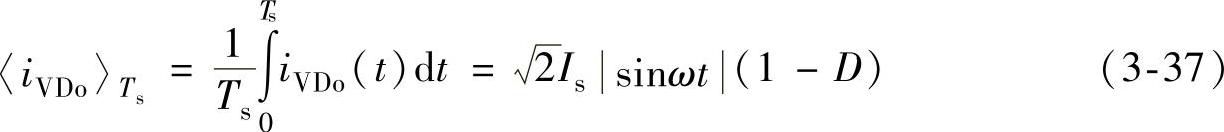
将式（3-31）代入式（3-37），得到

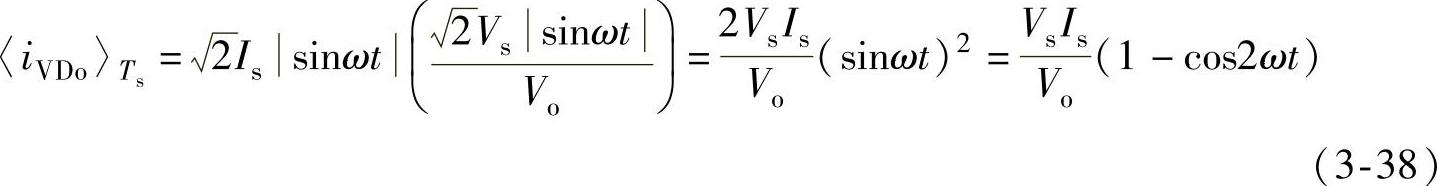
二极管VD的电流的低频部分存在一个直流分量和一个两倍于电源频率的交流分量。假定i_VDo中全部谐波电流均流入输出端滤波电容C，这样由式（3-38）可以得到电容电流i_C的两倍于电源频率的分量的幅值为

由于开关频率电流分量的频率比较高，因此它对滤波电容的电压脉动的影响较小，输出电压脉动主要是由两倍于电源频率的分量引起的。输出电压的脉动的幅值为

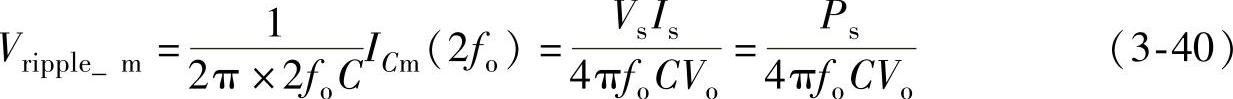
式中，P_s为PFC电路的输入功率，P_s=V_sI_s。

式（3-40）表明，滤波电容的电容量愈大，输出电压的脉动就愈小。输出电压的低频脉动实际上是由于输入电网瞬时功率和输出瞬时功率不平衡造成的。输入电网瞬时功率为

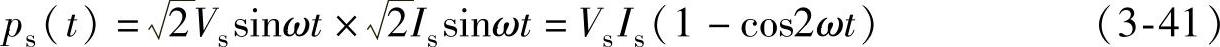
从上式可见，输入瞬时功率中包含一个2倍电源频率的交流分量，而我们希望PFC电路输出是一个稳定的直流，也即希望输出瞬时功率为p_o（t）=V_oI_o，这样输入瞬时功率与输出瞬时功率就存在不平衡，因此需要在PFC电路中增设一个储能环节，临时储存输入与输出之间存在的不平衡能量，输出滤波电容正是担当这一角色。由于输出滤波电容的容量有限，无法瞬间完成不平衡能量的充、放电，这样随着充、放电的进行，在电容两端必然引起电压的脉动。