确定临界应力总图中的λp和λs值

根据三种压杆的临界应力表达式，在Oσcrλ坐标系中可以做出σcr－λ关系曲线，称为临界应力总图，如图9-8所示。

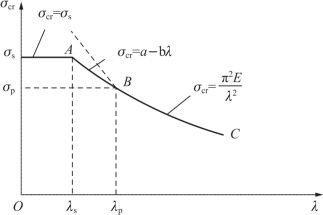
图9-8　临界应力总图

根据临界应力总图中所示之σcr－λ关系，可以确定区分不同材料三类压杆的长细比极限值λp、λs。

令细长杆的临界应力等于材料的比例极限（图9-8中的B点），得到

对于不同的材料，由于E、σp各不相同，λp的数值亦不相同。一旦给定E、σp，即可算得λp。例如，对于Q235钢，E＝206GPa，σp＝200Mpa。由式（9-19）算得λp＝101。

若令中长杆的临界应力等于屈服强度（图9-8中的A点），得到

例如，对于Q235钢，σs＝235Mpa，a＝304Mpa，b＝1.12Mpa，由式（9-20）可以算得λs＝61.6。

【例9-1】　图9-9（a）、（b）中所示压杆，其直径均为d，材料都是Q235钢，但两者长度和约束条件各不相同。

图9-9　例9-1图

（1）分析哪一根杆的临界荷载较大。

（2）计算d＝160mm，E＝206GPa时，杆的临界荷载。

解：（1）计算长细比，判断哪一根杆的临界荷载大

因为λ＝μl/i，其中i＝，而两者均为圆截面且直径相同，故有

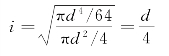
因两者约束条件和杆长都不相同，所以λ也不一定相同。

对于两端铰支的压杆[图9-9（a）]，μ＝1，l＝5m，

对于两端固定的压杆[图9-9（b）]，μ＝0.5，l＝9，(www.xing528.com)

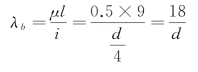
可见本例中两端铰支压杆的临界荷载小于两端固定压杆的临界荷载。

（2）计算各杆的临界荷载

对于两端铰支的压杆，

属于细长杆，利用欧拉公式计算临界力，

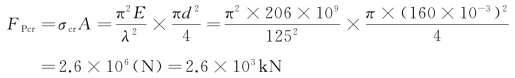
对于两端固定的压杆，

也属于细长杆，

【例9-2】　Q235钢制成的矩形截面杆，两端约束以及所承受的压缩荷载如图9-10所示[图9-10（a）为正视图；图9-10（b）为俯视图]，在A、B两处为销钉连接。若已知l＝2300mm，b＝40mm，h＝60mm，材料的弹性模量E＝205GPa。试求此杆的临界荷载。

图9-10　例9-2图

解：给定的压杆在A、B两处为销钉连接，这种约束与球铰约束不同。在正视图平面内屈曲时，A、B两处可以自由转动，相当于铰链；而在俯视图平面内屈曲时，A、B二处不能转动，这时可近似视为固定端约束。又因为是矩形截面，压杆在正视图平面内屈曲时，截面将绕z轴转动；而在俯视图平面内屈曲时，截面将绕y轴转动。

根据以上分析，为了计算临界力，应首先计算压杆在两个平面内的长细比，以确定它将在哪一平面内发生屈曲。

在正视图平面[图9-10（a）]内：

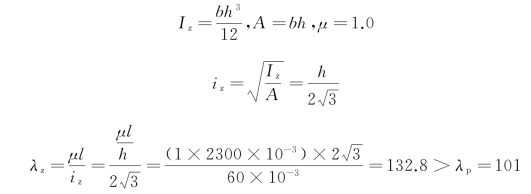
在俯视图平面[图9-10（b）]内：

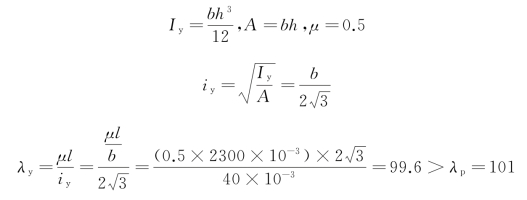
比较上述结果，可以看出λz＞λy，所以压杆将在正视图平面内屈曲。又因为在这一平面内，压杆的长细比λz＞λp，属于细长杆，可以用欧拉公式计算压杆的临界荷载：