
图8-13 与截面边界相切
在图8-8(a)中,若外力F是压力,即指向端面,称为偏心压缩。在土建工程中,混凝土以及砖石建筑物的立柱等均是承受偏心压缩的构件。混凝土以及砖石等材料抗拉强度低,抗压强度高,希望在这种立柱中只有压应力而无拉应力。由于中性轴是截面上拉、压应力的分界线,为使截面上只有压应力,必须使中性轴不处在截面的范围内,其极限情况是与截面边界相切(图8-13)。由式(8-11)知,中性轴的位置完全由偏心外力F作用点A(yF,zF)的位置所决定。所以,若使截面只有压应力,必须控制偏心压力F作用点A(yF,zF)的位置在一定范围之内,该范围称为截面核心。这样,对于偏心压缩的杆件,只要保证压力作用在截面核心内,那么,横截面上就只有压应力,而无拉应力了。
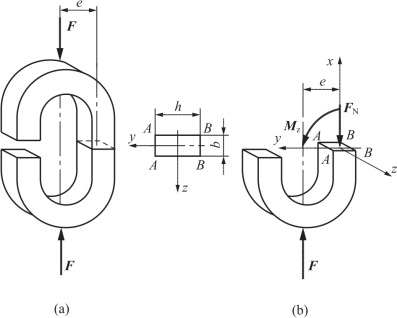
【例8-2】 矩形截面开口链环,受力与其他尺寸如图8-14(a)所示。已知:b=10mm、h=14mm、e=15mm、F=800N。试求:
(1)链环直段部分横截面上最大拉应力与最大压应力。
(2)若使直段部分横截面上均为压应力时,外力F作用线与直段部分截面形心的最大距离。
解:(1)计算链环直段部分横截面上最大拉、压应力。将链环从直段部分某一截面处截开,截面上将作用轴力FN、弯矩Mz两个内力分量[图8-14(b)]。

横截面上最大拉应力

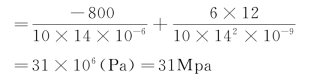
 (https://www.xing528.com)
(https://www.xing528.com)
图8-14 例8-2图
横截面上最大压应力
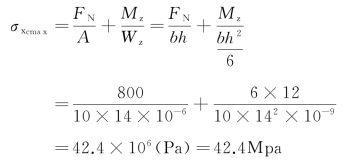
(2)最大距离。使中性轴向右平移与截面BB边重合,此时截面刚好只有压应力而无拉应力。为此,外力F作用线与该截面形心距离的yF、zF可由式(8-11)计算
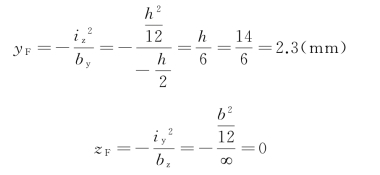
yF即使直段部分截面刚好只有压应力时,外力F作用线与该截面形心的最大距离。
【例8-3】 确定矩形截面的截面核心。
解:由例8-2知,对图8-15所示矩形截面,若使中性轴与BC边相切,则yF=h/6,zF=0,即点1(h/6,0)为外力作用点。同理可确定点2(-h/6,0)、点3(0,b/6)、点4(0,-b/6)也为外力作用点。现在考虑用什么曲线将这四点连接起来,从而得到该截面的截面核心。为此,考虑中性轴从BC边绕C点连续旋转到CD边,此时,与中性轴相对应的外力作用点将从点1连续移动到点3,这个运动轨迹就是这两点间的连线。C点是这些中性轴的共同点,将其坐标(-h/2,-b/2)代入式(8-6)中,即可得到连线方程式
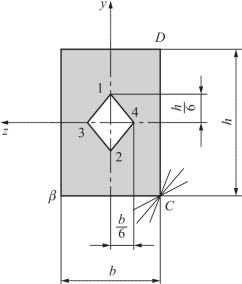
图8-15 矩形截面

上式说明点1到点3间连线是直线。同样,可得到点3到点2、点2到点4、点4到点1之间连线均为直线。于是得矩形截面的截面核心是个菱形面积,如图8-15所示。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




