使用叠加法求解弯曲变形问题

在弯曲变形很小，且材料服从胡克定律的情况下，挠曲线近似微分方程式（7-6）是弯矩的线性函数，弯矩与荷载的关系也是线性的。因此，对应于几种不同的荷载，弯矩可以叠加，因而方程式（7-6）的解也可叠加，即：当梁上同时作用几个荷载时，可分别求出每一荷载单独作用时引起的变形，然后把所得的变形叠加，即为这些荷载共同作用时的变形。这就是计算弯曲变形的叠加法。

【例7-4】　桥式起重大梁在自重q及吊重F作用下，其计算简图如图7-13（a）所示。试求大梁跨度中点的挠度和A截面的转角。

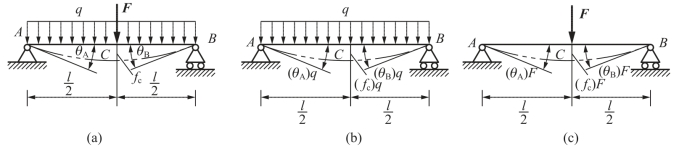
图7-13　例7-4图

解：大梁的变形是均布荷载q和集中力F共同引起的。在均布荷载q单独作用下[图7-13（b）]，大梁跨度中点的挠度和A截面的转角由表7-1第11栏查得为

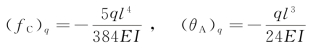
在集中力F单独作用下[见图7-13（c）]，大梁跨度中点C处的挠度和A截面的转角由表7-1第9栏查得为

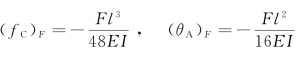
将荷载q[图7-13（b）]和集中力F[图7-13（c）]单独作用引起的变形叠加，得图7-13（a）所示大梁跨度中点的挠度和A截面的转角分别为

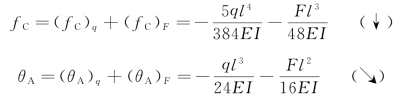
【例7-5】　用叠加法求图7-14（a）所示外伸梁外伸端的挠度和转角。设EI为常数。

解：可将图7-14（a）分解为图7-14（b）、（c）、（d）所示的三种情况的叠加。

在单一荷载作用下，自由端的转角和挠度可查表7-1得，

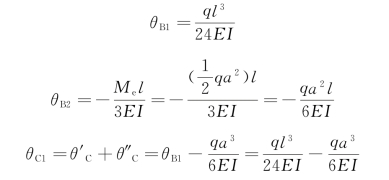
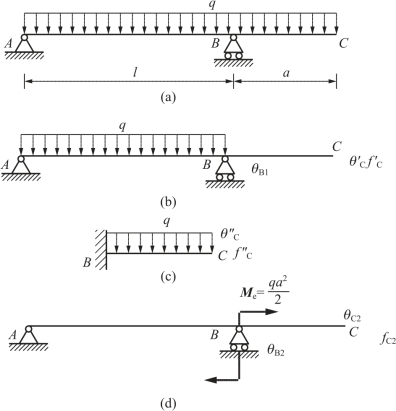
图7-14　例7-5图

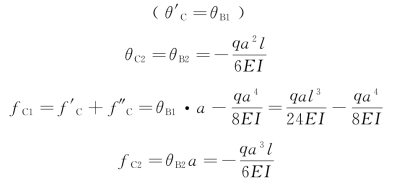(www.xing528.com)

在荷载q作用下，应用叠加法可得图7-14（a）的自由端的转角和挠度

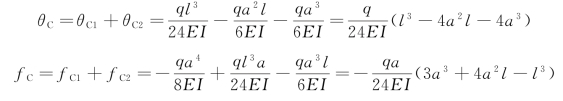
【例7-6】　一简支梁受力如图7-15（a）所示，求跨度中点C的挠度。

解：此题若用积分法求解，需要分三段积分，故计算起来是比较烦琐的。现在我们用叠加法求解。

由变形的对称性看出，跨度中点截面C的转角为零，挠曲线在C点的切线是水平的。故可以把梁的CB段看成悬臂梁[图7-15（b）]，自由端B的挠度|fB|也就等于原来AB梁的跨度中点挠度|fC|，而|fB|可用叠加法求出。

由叠加原理可知，图7-15（b）中所示两个荷载共同作用下引起的B点挠度，等于两个荷载分别单独作用时，引起B点挠度的代数和[图7-15（c）、（d）]。

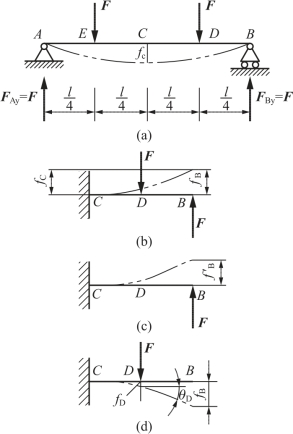
图7-15　例7-6图

由表7-1第3栏可知，由作用在B点荷载所引起B点挠度为

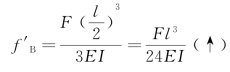
由作用在D点荷载所引起B点的挠度为

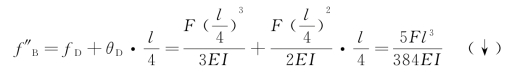
叠加f′B和f″B，得B点最终挠度为

因此有

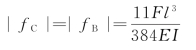
显然C点挠度向下。