本节将推导矩形截面梁的切应力计算公式。
矩形截面梁的切应力公式的推导,是在讨论正应力的基础上并采用了下列两条假设的前提下进行的。
(1)截面上各点切应力的方向都平行于截面上的剪力FS。
(2)切应力沿截面宽度均匀分布,即距中性轴等距离各点的切应力相等。
由弹性力学进一步的研究可知,以上两条假设,对于高度大于宽度的矩形截面是足够准确的。有了这两条假设,使切应力的研究大为简化,仅通过静力平衡条件,即可导出切应力的计算公式。
图6-15所示为承受任意荷载的矩形截面梁,截面高为h、宽为b。在梁上任取一横截面a-a,现研究该截面上距中性轴为y的水平线cc′处的切应力。根据上述假设可知,cc′线上各点的切应力大小相等,方向都平行于y轴。
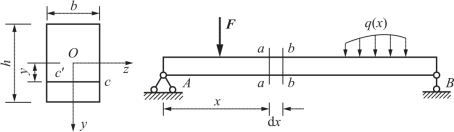
图6-15 承受任意荷载的矩形截面梁
通过a-a与b-b两个横截面截取一微段梁,微段梁的长度为dx。我们先分析一下该微段梁两侧面上的内力和应力情况。两侧面上的内力如图6-16(a)所示:左侧a-a截面上存在剪力FS和弯矩M(假定内力均为正),右侧截面上的剪力和弯矩为FS和M+dM。因微段梁上没有横向荷载,所以右侧截面上的剪力与左侧上的相同,仍为FS。由于左、右两截面的位置相差dx,因此右侧截面上的弯矩比左侧上多一增量dM。微段梁上的应力情况如图6-16(b)所示:两侧面都存在切应力与正应力,切应力的方向与剪力FS一致;正应力中性轴以下为拉应力,以上为压应力。由于b-b截面上的弯矩M+dM大于a-a截面上的弯矩M,所以b-b截面上的正应力大于a-a截面上相应位置的正应力。
现目的是要计算a-a截面cc′水平线上各点的切应力τ,但直接求τ有困难,不容易把切应力与内力联系起来。所以,采用如下办法:用过cc′的水平面将微段梁截开,并保留下部脱离体[图6-16(c)],由于脱离体侧面上存在竖向切应力τ,根据切应力互等定理可知,在脱离体的顶面(cc′dd′)上一定存在切应力τ′,且τ′=τ,如果能求得τ′,也就求得了τ。
切应力τ′可通过脱离体的平衡条件求得。作用在脱离体上的力如图6-16(d)所示(脱离体上的竖向力未画,因只需列∑Fx=0)。FN1和FN2分别代表左侧和右侧面上法向内力的总和,dFS代表顶面上水平切应力的总和。由平衡条件∑Fx=0,得
![]()
合力FN1可通过积分求得
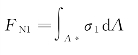
式中,σ1dA为脱离体左侧微面积dA上的法向合力,A∗为脱离体左侧面的面积。将σ1=M·y1/Iz代入上式,得
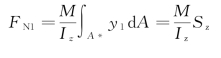
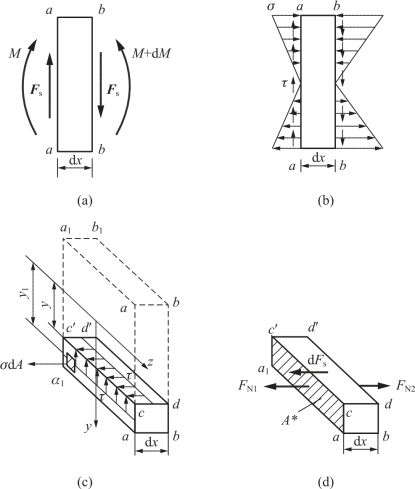
图6-16 微段梁两侧面上的内力和应力
式中
![]()
为脱离体侧面面积A∗对截面中性轴(z轴)的静矩。
同理可得
![]()
由于微段梁的长度很小,脱离体顶面上的切应力可认为是均匀分布的,所以
![]()
将FN1、FN2和dFS代入式(6-10),得
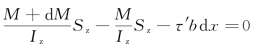 (https://www.xing528.com)
(https://www.xing528.com)
经整理得
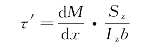
式中,![]() =FS将其代入上式得
=FS将其代入上式得
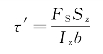
因
![]()
所以

式(6-11)就是矩形截面梁横截面上任一点的切应力计算公式。式中FS为横截面上的剪力;Iz为截面对中性轴的惯性矩;b为截面的宽度;Sz为面积A∗对中性轴的静矩。A∗是过欲求应力点的水平线到截面边缘间的面积。
剪力FS和静矩Sz均为代数量,但在利用式(6-11)计算切应力时,FS与Sz均以绝对值代入,切应力的方向可依剪力的方向来确定(τ与FS的方向一致)。
下面讨论切应力沿截面高度的分布规律。对某一截面来说,式(6-11)中的FS、Iz、b均为常量,只有静矩Sz随欲求应力的点到中性轴的距离y而变化。面积A∗对中性轴的静矩为
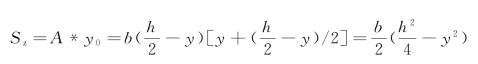
将上式及Iz=![]() 代入式(6-11),得
代入式(6-11),得
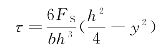
此式表明,切应力沿截面高度按二次抛物线规律变化(图6-17)。当y=±![]() 时,τ=0,即上、下边缘处切应力等于零。当y=0时,τ=τmax,即中性轴上切应力最大(这与正应力的分布规律恰好相反)。中性轴上的最大切应力为
时,τ=0,即上、下边缘处切应力等于零。当y=0时,τ=τmax,即中性轴上切应力最大(这与正应力的分布规律恰好相反)。中性轴上的最大切应力为
![]()
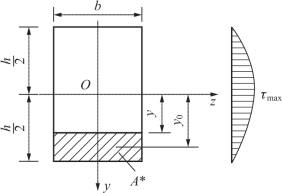
图6-17 切应力沿截面高度按二次抛物线规律变化
即矩形截面上的最大切应力为截面上平均切应力的1.5倍。
【例6-6】 一矩形截面简支梁如图6-18所示,已知l=3m,h=160mm,b=100mm,h1=40mm,F=3kN。试求m-m截面上K点的切应力。
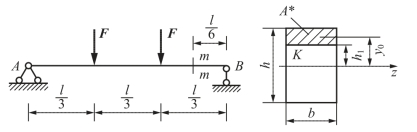
图6-18 例6-6图
解:求得m-m截面上的剪力为3kN,截面的惯性矩及面积A∗对中性轴的静矩分别为
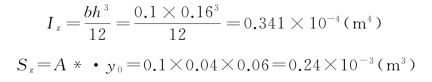
K点的切应力为
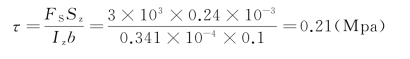
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




