梁的正应力强度条件及应用

为了保证梁的安全工作，梁内的最大正应力不能超过一定的限度。有了正应力公式后，就可算出梁中的最大正应力，从而建立正应力强度条件，对梁进行强度计算。

对梁的某一截面来说，最大正应力发生在距中性轴最远的位置，其值为

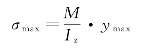
对全梁（等截面梁）来说，最大正应力发生在弯矩最大的截面上，其值为

将此式改写为

令

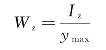
则

根据强度要求，同时考虑留有一定的安全储备，梁内的最大正应力不能超过材料的许用应力，因而有

上式就是梁的正应力强度条件。式中[σ]为弯曲时材料的许用正应力，其值随材料的不同而不同，在有关规范中均有具体规定。Wz称为弯曲截面系数，或抗弯截面系数，它与梁的截面形状和尺寸有关。Wz反映截面形状和尺寸对弯曲强度的影响，显然，Wz值越大，从强度角度看，就越有利。

对矩形截面

对圆形截面

对工字钢、槽钢、角钢等型钢截面，Wz值可在型钢表中查得。

利用式（6-8）的强度条件，可解决工程中常见的下列三类问题。

（1）强度校核。当已知梁的截面形状和尺寸，梁所用的材料及梁上荷载时，可校核梁是否满足强度要求。即校核是否满足下列关系

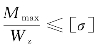
（2）选择截面。当已知梁所用的材料及梁上荷载时，可根据强度条件，先算出所需的弯曲截面系数，即

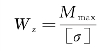
然后，依所选的截面形状，再由Wz值确定截面的尺寸。

（3）计算梁所能承受的最大荷载。当已知梁所用的材料、截面的形状和尺寸时，根据强度条件，先算出梁所能承受的最大弯矩，即

再由Mmax与荷载的关系，算出梁所能承受的最大荷载。

下面举例说明正应力强度条件的具体应用。

【例6-2】　一矩形截面的简支木梁，梁上作用有均布荷载（图6-7），已知：l＝4m，b＝140mm，h＝210mm，q＝2kN/m，弯曲时木材的许用正应力[σ]＝10Mpa。试校核该梁的强度。

图6-7　例6-2图

解：梁中的最大正应力发生在跨中弯矩最大的截面上，最大弯矩为

弯曲截面系数为

最大正应力为

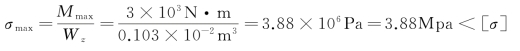
所以满足强度要求。

【例6-3】　就例6-2，试求梁能承受的最大荷载（即求qmax）。(www.xing528.com)

解：根据强度条件，梁能承受的最大弯矩为

跨中最大弯矩与荷载q的关系为

所以

从而得

即梁能承受的最大荷载为qmax＝5.15kN/m。

上面是根据强度条件求最大荷载的一般方法。对此例来说，在例6-2中，已求得在q＝2kN/m时的最大正应力σmax＝2.91Mpa，根据应力与荷载成正比（在弹性范围内），最大荷载也可通过下式求得，即

则

【例6-4】　简支梁上作用两个集中力（图6-8），已知l＝6m，F1＝15kN，F2＝21kN。如果梁采用热轧普通工字钢，钢的许用应力[σ]＝170Mpa，试选择工字钢的型号。

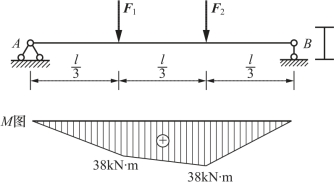
图6-8　例6-4图

解：先画出弯矩图，最大弯矩发生在F2作用截面上，其值为38kN·m。根据强度条件，梁所需的弯曲截面系数为

根据算得的Wz值，在附录型钢表上查出与该值相近的型号，就是我们所需的型号。在附录的型钢表中，20a号工字钢的Wz值为237cm3，与算得的Wz值相近，故选取20a号工字钢。因20a号的Wz值大于按强度条件算得的Wz值，所以一定满足强度条件。如选取的工字钢的Wz值略小于按强度条件算得的Wz值时，则应再校核一下强度，当σmax不超过[σ]的5%时，还是可以用的，是工程中所允许的。

【例6-5】　T形截面的外伸梁如图6-9所示，已知l＝600mm，a＝40mm，b＝30mm，c＝80mm，F1＝24kN，F2＝9kN，材料的许用拉应力[σt]＝30Mpa，许用压应力[σc]＝90Mpa。试校核梁的强度。

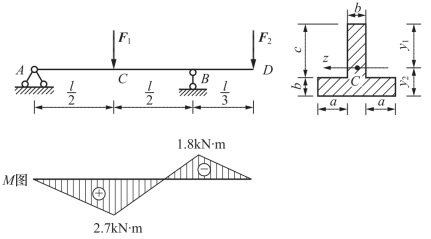
图6-9　例6-5图

解：先画出弯矩图。截面为T字形，需算出形心C的位置及截面对中性轴的惯性矩，算得结果为

因材料的抗拉与抗压性能不同，截面对中性轴又不对称，所以需对最大拉应力与最大压应力分别进行校核。

（1）校核最大拉应力

首先要分析最大拉应力发生在哪里。由于截面对中性轴不对称，而正、负弯矩又都存在，因此，最大拉应力不一定发生在弯矩绝对值最大的截面上。应该对最大正弯矩和最大负弯矩两个截面上的拉应力进行分析比较。在最大正弯矩的C截面上，最大拉应力发生在截面的下边缘，其值为

在最大负弯矩的B截面上，最大拉应力发生在截面的上边缘，其值为

在上面两式中，MC＞MB而y2＜y1，应比较MCy2与MBy1

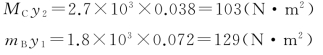
因MBy1＞MCy2，所以最大拉应力发生在B截面上，即

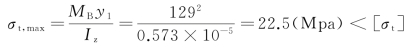
满足强度要求。

（2）校核最大压应力

首先确定最大压应力发生在哪里。与分析最大拉应力一样，要比较C、B两个截面。C截面上最大压应力发生在上边缘，B截面上的最大压应力发生在下边缘。因MC与y1分别大于MB与y2，所以最大压应力一定发生在C截面上。即

满足强度要求。